V tejto lekcii sa naučíme používať vzorce a pravidlá diferenciácie.

Príklady. Nájdite derivácie funkcií.

1. y = x 7 + x 5 - x 4 + x 3 - x 2 + x - 9. Uplatnenie pravidla ja, vzorce 4, 2 a 1. Dostaneme:

y’=7x 6 +5x4-4x3+3x2-2x+1.

2. y=3x6-2x+5. Riešime podobne, pomocou rovnakých vzorcov a vzorca 3.

y’=3∙6x 5-2=18x 5-2.

Uplatnenie pravidla ja, vzorce 3, 5 A 6 A 1.

Uplatnenie pravidla IV, vzorce 5 A 1 .

V piatom príklade podľa pravidla ja derivácia súčtu sa rovná súčtu derivácií a práve sme našli deriváciu 1. člena (príklad 4 ), preto nájdeme deriváty 2 A 3 podmienky a za 1 summand môžeme hneď napísať výsledok.

Poďme rozlišovať 2 A 3 termíny podľa vzorca 4 . Aby sme to dosiahli, transformujeme korene tretej a štvrtej mocniny v menovateli na mocniny so zápornými exponentmi a potom podľa 4 formule, nájdeme deriváty mocnín.

Pozrite si tento príklad a výsledok. Zachytili ste vzor? Dobre. To znamená, že máme nový vzorec a môžeme ho pridať do našej tabuľky derivátov.

Vyriešme šiesty príklad a odvodíme ďalší vzorec.

Využime pravidlo IV a vzorec 4 . Výsledné zlomky zredukujeme.

Poďme sa pozrieť na túto funkciu a jeho derivát. Vy, samozrejme, rozumiete vzoru a ste pripravení pomenovať vzorec:

Učte sa nové vzorce!

Príklady.

1. Nájdite prírastok argumentu a prírastok funkcie y= x 2, ak bola počiatočná hodnota argumentu rovná 4 a nové - 4,01 .

Riešenie.

Nová hodnota argumentu x=x 0 +Δx. Dosadíme údaje: 4,01=4+Δх, teda prírastok argumentu Δx= 4,01-4 = 0,01. Prírastok funkcie sa podľa definície rovná rozdielu medzi novou a predchádzajúcou hodnotou funkcie, t.j. Ay=f (x 0 + Ax) - f (x 0). Keďže máme funkciu y=x2, To Δу=(x 0 +Δx) 2 - (x 0) 2 =(x 0) 2 +2x 0 · Δx+(Δx) 2 - (x 0) 2 = 2x 0 · Δx+(Δx) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

odpoveď: prírastok argumentov Δx=0,01; prírastok funkcie Δу=0,0801.

Prírastok funkcie možno nájsť inak: Δy=y(x0+Ax)-y(x0)=y(4,01)-y(4)=4,012-42=16,0801-16=0,0801.

2. Nájdite uhol sklonu dotyčnice ku grafu funkcie y=f(x) v bode x 0, Ak f "(x 0) = 1.

Riešenie.

Hodnota derivátu v bode dotyku x 0 a je hodnota tangens tangens uhla ( geometrický význam derivát). Máme: f "(x 0) = tanα = 1 → α = 45°, pretože tg45°=1.

odpoveď: dotyčnica ku grafu tejto funkcie zviera s kladným smerom osi Ox uhol rovný 45°.

3. Odvoďte vzorec pre deriváciu funkcie y=xn.

Diferenciácia je činnosť hľadania derivácie funkcie.

Pri hľadaní derivátov použite vzorce, ktoré boli odvodené na základe definície derivátu, rovnakým spôsobom, ako sme odvodili vzorec pre stupeň derivátu: (x n)" = nx n-1.

Toto sú vzorce.

Tabuľka derivátov Bude ľahšie zapamätať si vyslovovaním verbálnych formulácií:

1. Derivácia konštantnej veličiny je nulová.

2. X prvočíslo sa rovná jednej.

3. Konštantný faktor možno vyňať zo znamienka derivácie.

4. Derivácia stupňa sa rovná súčinu exponentu tohto stupňa o stupeň s rovnakým základom, ale exponent je o jeden menší.

5. Derivácia koreňa sa rovná jednej delenej dvoma rovnakými koreňmi.

6. Derivácia jedna delená x sa rovná mínus jedna delená x na druhú.

7. Derivácia sínusu sa rovná kosínusu.

8. Derivácia kosínusu sa rovná mínus sínusu.

9. Derivácia dotyčnice sa rovná jednej delenej druhou mocninou kosínusu.

10. Derivácia kotangensu sa rovná mínus jednej delenej druhou mocninou sínusu.

učíme pravidlá diferenciácie.

1. Derivácia algebraického súčtu sa rovná algebraickému súčtu derivátov členov.

2. Derivát súčinu sa rovná súčinu derivátu prvého a druhého faktora plus súčinu prvého faktora a derivátu druhého.

3. Derivácia „y“ delená „ve“ sa rovná zlomku, v ktorom je čitateľ „y prvočíslo vynásobené „ve“ mínus „y vynásobené prvočíslom ve“ a menovateľ je „ve na druhú“.

4. Špeciálny prípad vzorca 3.

Poďme sa spolu učiť!

Strana 1 z 1 1

Derivát je najdôležitejší pojem matematická analýza. Charakterizuje zmenu funkcie argumentu X v určitom okamihu. Okrem toho samotná derivácia je funkciou argumentu X

Derivácia funkcie v bode je limit (ak existuje a je konečný) pomeru prírastku funkcie k prírastku argumentu za predpokladu, že prírastok má tendenciu k nule.

Najčastejšie používané sú nasledujúce derivačný zápis :

Príklad 1 Využiť definícia derivátu, nájdite deriváciu funkcie

Riešenie. Z definície derivátu vyplýva nasledujúca schéma jeho výpočtu.

Dajme argumentu prírastok (delta) a nájdime prírastok funkcie:

Nájdite pomer prírastku funkcie k prírastku argumentu:

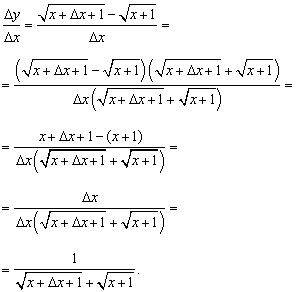
Vypočítajme limit tohto pomeru za predpokladu, že prírastok argumentu má tendenciu k nule, teda derivácii požadovanej v probléme:

Fyzikálny význam derivátu

TO pojem derivát vedená štúdiom práva Galilea Galileiho voľný pád telies, a v širšom zmysle - problém okamžitej rýchlosti nerovnomerného priamočiareho pohybu bodu.

Nechajte kamienok zdvihnúť a potom uvoľniť z pokoja. Cesta s prešiel v čase t, je funkciou času, tzn. s = s(t). Ak je daný zákon pohybu bodu, potom je možné určiť priemernú rýchlosť za ľubovoľné časové obdobie. Nech je v danom momente kamienok v pozícii A, a momentálne - v pozícii B. Počas určitého obdobia (od t to ) bod prešiel cestou . Preto priemerná rýchlosť pohybu za toto časové obdobie, ktorú označujeme , je

Pohyb voľne padajúceho telesa je však zjavne nerovnomerný. Rýchlosť v pád sa neustále zvyšuje. A priemerná rýchlosť už nestačí na charakterizáciu rýchlosti pohybu na rôznych úsekoch trasy. Čím je časový úsek kratší, tým je táto charakteristika presnejšia. Preto sa zavádza tento pojem: okamžitá rýchlosť priamočiareho pohybu (alebo rýchlosť v danom časovom okamihu t) sa nazýva priemerná povolená rýchlosť pri:

(za predpokladu, že táto hranica existuje a je konečná).

Ukazuje sa teda, že okamžitá rýchlosť je hranicou pomeru prírastku funkcie s(t) na prírastok argumentu t at Toto je derivát, ktorý v všeobecný pohľad sa píše takto:

Riešenie naznačeného problému je fyzický význam derivát . Takže derivácia funkcie y=f(X) v bode X sa nazýva limita (ak existuje a je konečná) prírastku funkcie k prírastku argumentu za predpokladu, že tento má tendenciu k nule.

Príklad 2 Nájdite deriváciu funkcie

Riešenie. Z definície derivátu vyplýva nasledujúca schéma jeho výpočtu.

Krok 1. Zvýšme argument a nájdime

Krok 2. Nájdite prírastok funkcie:

Krok 3. Nájdite pomer prírastku funkcie k prírastku argumentu:

Krok 4. Vypočítajte limit tohto pomeru v , čiže deriváciu:

Geometrický význam derivácie

Nech je funkcia definovaná na intervale a nech je bod M na grafe funkcie zodpovedá hodnote argumentu a bodu R– význam. Poďme kresliť cez body M A R priamku a nazvite ju sekanta. Označme uhlom medzi sečnicou a osou. Je zrejmé, že tento uhol závisí od .

Ak existuje

prechod cez bod sa nazýva medzná poloha sečny PÁN o (alebo o ).

Tangenta ku grafu funkcie v bode M nazývaná limitná poloha sečny PÁN at , or , ktorý je rovnaký v .

Z definície vyplýva, že na existenciu dotyčnice stačí, že existuje limita

a limit rovný uhlu sklon dotyčnice k osi.

Teraz dajme presná definícia dotyčnica.

Tangenta ku grafu funkcie v bode je priamka prechádzajúca bodom a majúca sklon, t.j. priamka, ktorej rovnica

Z tejto definície vyplýva, že derivácia funkcie rovná sklon dotyčnica ku grafu tejto funkcie v bode úsečky X. Toto je geometrický význam derivácie.

Nech je funkcia y = f(x) definovaná v intervale X. Derivát funkcia y = f(x) v bode x o sa nazýva limita

= .

Ak tento limit konečný, potom sa volá funkcia f(x). diferencovateľné v bode X o; Navyše sa v tomto bode ukazuje byť nevyhnutne kontinuálny.

Ak sa uvažovaná hranica rovná  (alebo - ), potom za predpokladu, že funkcia v bode X o je spojitá, povieme, že funkcia f(x) má v bode X o nekonečná derivácia.

Derivát je označený symbolmi

y , f (x o), , .

Nájdenie derivácie je tzv diferenciácie funkcie. Geometrický význam derivácie je, že derivácia je sklon dotyčnice ku krivke y=f(x) v danom bode X o ; fyzický význam - je, že derivácia dráhy vzhľadom na čas je okamžitá rýchlosť pohybujúceho sa bodu pri priamy pohyb s = s(t) v čase t o.

Ak s - konštantné číslo, a u = u(x), v = v(x) sú niektoré diferencovateľné funkcie, potom platia nasledujúce pravidlá diferenciácie:

1) (c) " = 0, (cu) " = cu";

2) (u+v)" = u"+v";

3) (uv)" = u"v+v"u;

4) (u/v)" = (u"v-v"u)/v2;

5) ak y = f(u), u = (x), t.j. y = f((x)) - komplexná funkcia alebo superpozícia, zložený z diferencovateľných funkcií  a f, potom , alebo

6) ak pre funkciu y = f(x) existuje inverzne diferencovateľná funkcia x = g(y) a  0, potom .

Na základe definície derivácie a pravidiel diferenciácie je možné zostaviť zoznam tabuľkových derivácií hlavných elementárnych funkcií.

1. (u )" =  u  1 u" (  R).

2. (a u)" = a u lna u".

3. (e u)" = e u u".

4. (log a u)" = u"/(u ln a).

5. (ln u)" = u"/u.

6. (sin u)" = cos u u".

7. (cos u)" = - hriech u u".

8. (tg u)" = 1/ cos 2 u u".

9. (ctg u)" = - u" / hriech 2 u.

10. (arcsin u)" = u" / .

11. (arccos u)" = - u" / .

12. (arctg u)" = u"/(1 + u 2).

13. (arcctg u)" = - u"/(1 + u 2).

Vypočítajme deriváciu mocninno-exponenciálneho výrazu y=u v , (u>0), kde u A v podstata funkcie z X, ktoré majú v danom bode deriváty ty",v".

Logaritmovaním rovnosti y=u v dostaneme ln y = v ln u.

Prirovnávanie derivátov vzhľadom na X z oboch strán výslednej rovnosti pomocou pravidiel 3, 5 a vzorca pre deriváciu logaritmickej funkcie budeme mať:

y"/y = vu"/u +v" ln u, odkiaľ y" = y (vu"/u +v" ln u).

(u v)"=u v (vu"/u+v" ln u), u > 0.

Napríklad, ak y = x sin x, potom y" = x sin x (sin x/x + cos x ln x).

Ak je funkcia y = f(x) v bode diferencovateľná X, t.j. má v tomto bode konečnú deriváciu y", potom = y"+, kde 0 pri х 0; teda  y = y" х +  x.

Volá sa hlavná časť prírastku funkcie, lineárna vzhľadom na x diferenciál funkcie a označuje sa dy: dy = y" х. Ak do tohto vzorca dáme y=x, dostaneme dx = x"х = 1х =х, teda dy=y"dx, t.j. symbol pretože Derivačný zápis si možno predstaviť ako zlomok.

Prírastok funkcie  r je prírastok súradnice krivky a diferenciál d r je prírastok ordináty dotyčnice.

Nájdite pre funkciu y=f(x) jej deriváciu y = f (x). Derivát tohto derivátu je tzv derivát druhého rádu funkcie f(x), príp druhá derivácia, a je určený .

Nasledujúce sú definované a označené rovnakým spôsobom:

derivát tretieho rádu - ,

derivát štvrtého rádu -

a všeobecne povedané derivát n-tého rádu - .

Príklad 3.15. Vypočítajte deriváciu funkcie y=(3x 3 -2x+1)sin x.

Riešenie. Podľa pravidla 3 y"=(3x 3 -2x+1)"hriech x + (3x 3 -2x+1)(hriech x)" = = (9x 2 -2)hriech x + (3x 3 -2x +1) cos x.

Príklad 3.16 . Nájdite y", y = tan x + .

Riešenie. Pomocou pravidiel na diferenciáciu súčtu a kvocientu dostaneme: y"=(tgx + )" = (tgx)" + ()" = + = .

Príklad 3.17. Nájdite deriváciu komplexnej funkcie y= , u=x 4 +1.

Riešenie. Podľa pravidla diferenciácie komplexnej funkcie dostaneme: y" x =y " u u" x =()" u (x 4 +1)" x =(2u +. Keďže u=x 4 +1, potom (2 x 4 + 2+ .

Prvá úroveň

Derivácia funkcie. Komplexný sprievodca (2019)

Predstavme si rovnú cestu prechádzajúcu kopcovitou oblasťou. To znamená, že ide hore a dole, ale nezatáča doprava ani doľava. Ak je os nasmerovaná horizontálne pozdĺž cesty a vertikálne, potom bude čiara cesty veľmi podobná grafu nejakej spojitej funkcie:

Os je určitá úroveň nulovej nadmorskej výšky; v živote ako to používame hladinu mora.

Keď sa po takejto ceste pohybujeme vpred, pohybujeme sa aj nahor alebo nadol. Môžeme tiež povedať: keď sa argument zmení (pohyb po vodorovnej osi), zmení sa hodnota funkcie (pohyb po zvislej osi). Teraz sa zamyslime nad tým, ako určiť „strmosť“ našej cesty? Aká by to mohla byť hodnota? Je to veľmi jednoduché: ako veľmi sa zmení výška pri pohybe vpred o určitú vzdialenosť. Na rôznych úsekoch cesty, keď sa posunieme vpred (pozdĺž osi x) o jeden kilometer, budeme stúpať alebo klesať o rôzne množstvá metrov vzhľadom na hladinu mora (pozdĺž osi y).

Označme pokrok (čítaj „delta x“).

Grécke písmeno (delta) sa bežne používa v matematike ako predpona s významom „zmena“. To je - to je zmena množstva, - zmena; čo je potom? Správne, zmena veľkosti.

Dôležité: výraz je jeden celok, jedna premenná. Nikdy neoddeľujte „delta“ od „x“ alebo akéhokoľvek iného písmena! To je napríklad .

Takže sme sa posunuli horizontálne dopredu. Ak porovnáme čiaru cesty s grafom funkcie, ako potom označíme stúpanie? Určite,. To znamená, že keď napredujeme, stúpame vyššie.

Hodnota sa dá ľahko vypočítať: ak sme na začiatku boli vo výške a po presťahovaní sme sa ocitli vo výške, potom. Ak je koncový bod nižšie ako začiatočný bod, bude záporný – to znamená, že nestúpame, ale klesáme.

Vráťme sa k „strmosti“: toto je hodnota, ktorá ukazuje, o koľko (strmšie) sa výška zväčší pri pohybe dopredu o jednu jednotku vzdialenosti:

Predpokladajme, že na niektorom úseku cesty sa pri posune vpred o kilometer cesta zdvihne o kilometer. Potom je sklon na tomto mieste rovnaký. A ak cesta pri pohybe vpred o m klesla o km? Potom je sklon rovnaký.

Teraz sa pozrime na vrchol kopca. Ak si vezmete začiatok úseku pol kilometra pred vrcholom a koniec pol kilometra za ním, môžete vidieť, že výška je takmer rovnaká.

To znamená, že podľa našej logiky sa ukazuje, že sklon je tu takmer rovný nule, čo zjavne nie je pravda. Len na vzdialenosť niekoľkých kilometrov sa môže veľa zmeniť. Pre adekvátnejšie a presnejšie posúdenie strmosti je potrebné zvážiť menšie plochy. Ak napríklad zmeriate zmenu výšky pri pohybe o jeden meter, výsledok bude oveľa presnejší. Ale ani táto presnosť nám nemusí stačiť – veď ak je v strede cesty stĺp, jednoducho ho prejdeme. Akú vzdialenosť by sme teda mali zvoliť? Centimeter? Milimeter? Menej je lepšie!

IN skutočný život Meranie vzdialeností s presnosťou na milimeter je viac než dosť. Ale matematici sa vždy snažia o dokonalosť. Preto bol vynájdený koncept nekonečne malý, to znamená, že absolútna hodnota je menšia ako akékoľvek číslo, ktoré vieme pomenovať. Napríklad poviete: jeden bilión! O koľko menej? A toto číslo vydelíte - a bude ešte menej. A tak ďalej. Ak chceme napísať, že množstvo je nekonečne malé, napíšeme takto: (čítame „x má tendenciu k nule“). Je veľmi dôležité pochopiť že toto číslo nie je nula! Ale veľmi blízko k tomu. To znamená, že ním môžete deliť.

Pojem opačný k nekonečne malému je nekonečne veľký (). Pravdepodobne ste sa s tým už stretli, keď ste pracovali na nerovnostiach: toto číslo je modulo väčšie ako akékoľvek číslo, ktoré si dokážete predstaviť. Ak prídete na najväčšie možné číslo, jednoducho ho vynásobte dvomi a dostanete ešte väčšie číslo. A nekonečno je ešte väčšie ako to, čo sa deje. V skutočnosti sú nekonečne veľké a nekonečne malé navzájom inverzné, teda at, a naopak: at.

Teraz sa vráťme na našu cestu. Ideálne vypočítaný sklon je sklon vypočítaný pre nekonečne malý segment cesty, to znamená:

Podotýkam, že pri nekonečne malom posune bude aj zmena výšky nekonečne malá. Dovoľte mi však pripomenúť, že nekonečne malý neznamená rovný nule. Ak rozdelíte nekonečne malé čísla navzájom, môžete získať celkom bežné číslo, Napríklad, . To znamená, že jedna malá hodnota môže byť presne krát väčšia ako druhá.

Načo to všetko je? Cesta, strmosť... Nejdeme na automobilovú rely, ale učíme matematiku. A v matematike je všetko úplne rovnaké, len sa inak volá.

Koncept derivátu

Derivácia funkcie je pomer prírastku funkcie k prírastku argumentu pre nekonečne malý prírastok argumentu.

Postupne v matematike nazývajú zmena. Rozsah, v akom sa argument () mení, keď sa pohybuje pozdĺž osi, sa nazýva prírastok argumentov a je určený.O koľko sa zmenila funkcia (výška) pri pohybe vpred pozdĺž osi o vzdialenosť sa nazýva prírastok funkcie a je určený.

Derivácia funkcie je teda pomer k kedy. Deriváciu označujeme rovnakým písmenom ako funkcia, len s prvočíslom vpravo hore: alebo jednoducho. Takže napíšme odvodený vzorec pomocou týchto zápisov:

Rovnako ako v analógii s cestou, aj tu, keď sa funkcia zvyšuje, derivácia je kladná, a keď klesá, je záporná.

Môže sa derivácia rovnať nule? určite. Napríklad, ak ideme po rovnej vodorovnej ceste, strmosť je nulová. A je pravda, že výška sa vôbec nemení. Tak je to aj s deriváciou: derivácia konštantnej funkcie (konštanta) sa rovná nule:

keďže prírastok takejto funkcie je rovný nule pre ľubovoľnú.

Spomeňme si na príklad z kopca. Ukázalo sa, že je možné usporiadať konce segmentu pozdĺž rôzne strany zhora, takže výška na koncoch je rovnaká, to znamená, že segment je rovnobežný s osou:

Ale veľké segmenty sú znakom nepresného merania. Zdvihneme náš segment nahor rovnobežne so sebou, potom sa jeho dĺžka zníži.

Nakoniec, keď sme nekonečne blízko vrcholu, dĺžka segmentu bude nekonečne malá. Zároveň však zostal rovnobežný s osou, to znamená, že rozdiel vo výškach na jej koncoch je rovný nule (nemá tendenciu, ale rovná sa). Takže derivát

Dá sa to chápať takto: keď stojíme na samom vrchole, malý posun doľava alebo doprava zmení našu výšku zanedbateľne.

Existuje aj čisto algebraické vysvetlenie: vľavo od vrcholu sa funkcia zvyšuje a vpravo klesá. Ako sme už skôr zistili, keď funkcia rastie, derivácia je kladná, a keď klesá, je záporná. Mení sa ale plynulo, bez skokov (keďže cesta nikde prudko nemení sklon). Preto medzi negatívnymi a kladné hodnoty tam určite musí byť. Bude to tam, kde sa funkcia ani nezväčšuje, ani neznižuje – v bode vrcholu.

To isté platí pre žľab (oblasť, kde funkcia vľavo klesá a vpravo sa zvyšuje):

Trochu viac o prírastkoch.

Takže zmeníme argument na veľkosť. Z akej hodnoty sa meníme? Čo sa z toho (argument) stalo teraz? Môžeme si vybrať ľubovoľný bod a teraz z neho budeme tancovať.

Zvážte bod so súradnicou. Hodnota funkcie v ňom je rovnaká. Potom urobíme rovnaký prírastok: zväčšíme súradnicu o. Aký je teraz argument? Veľmi ľahké: . Akú hodnotu má funkcia teraz? Kam smeruje argument, tam je aj funkcia: . A čo zvýšenie funkcie? Nič nové: toto je stále suma, o ktorú sa funkcia zmenila:

Precvičte si nájdenie prírastkov:

Nájdite prírastok funkcie v bode, v ktorom je prírastok argumentu rovný.
To isté platí pre funkciu v bode.

Riešenia:

V rôznych bodoch s rovnakým prírastkom argumentov bude prírastok funkcie odlišný. To znamená, že derivácia v každom bode je iná (rozoberali sme to úplne na začiatku – strmosť cesty je v rôznych bodoch rôzna). Preto, keď píšeme derivát, musíme uviesť, v ktorom bode:

Funkcia napájania.

Mocninná funkcia je funkcia, ktorej argument je do určitej miery (logický, však?).

Navyše - v akomkoľvek rozsahu: .

Najjednoduchší prípad je, keď je exponent:

Nájdite jeho derivát v bode. Pripomeňme si definíciu derivátu:

Takže argument sa mení z na. Aký je prírastok funkcie?

Prírastok je toto. Ale funkcia v ktoromkoľvek bode sa rovná jej argumentu. Preto:

Derivát sa rovná:

Derivácia sa rovná:

b) Teraz zvážte kvadratickej funkcie (): .

Teraz si to pripomeňme. To znamená, že hodnotu prírastku možno zanedbať, pretože je nekonečne malá, a preto je na pozadí druhého výrazu nevýznamná:

Tak sme prišli s ďalším pravidlom:

c) Pokračujeme v logickom rade: .

Tento výraz je možné zjednodušiť rôznymi spôsobmi: otvorte prvú zátvorku pomocou vzorca na skrátené násobenie kocky súčtu alebo celý výraz rozložte pomocou vzorca rozdielu kociek. Skúste to urobiť sami pomocou ktorejkoľvek z navrhovaných metód.

Takže som dostal nasledovné:

A opäť si to pripomeňme. To znamená, že môžeme zanedbať všetky výrazy obsahujúce:

Dostaneme: .

d) Podobné pravidlá možno získať pre veľké právomoci:

e) Ukazuje sa, že toto pravidlo možno zovšeobecniť pre mocninnú funkciu s ľubovoľným exponentom, dokonca ani nie celým číslom:

(2)

Pravidlo možno formulovať slovami: „stupeň sa posunie dopredu ako koeficient a potom sa zníži o .

Toto pravidlo si preukážeme neskôr (takmer na samom konci). Teraz sa pozrime na niekoľko príkladov. Nájdite deriváciu funkcií:

(dvoma spôsobmi: vzorcom a pomocou definície derivácie - výpočtom prírastku funkcie);

. Verte alebo nie, toto je mocenská funkcia. Ak máte otázky typu „Ako to je? Kde je titul?“, zapamätajte si tému „“!
Áno, áno, koreň je tiež stupeň, len zlomkový: .
Takže náš Odmocnina- toto je len stupeň s indikátorom:
.
Hľadáme derivát pomocou nedávno naučeného vzorca:
Ak to bude v tomto bode opäť nejasné, zopakujte tému „“!!! (asi stupeň so záporným exponentom)
. Teraz exponent:
A teraz cez definíciu (ešte ste zabudli?):
;
.
Teraz, ako obvykle, zanedbávame výraz obsahujúci:
.
. Kombinácia predchádzajúcich prípadov: .

Goniometrické funkcie.

Tu použijeme jeden fakt z vyššej matematiky:

S výrazom.

Dôkaz sa naučíte v prvom ročníku inštitútu (a aby ste sa tam dostali, musíte dobre zložiť jednotnú štátnu skúšku). Teraz to ukážem graficky:

Vidíme, že keď funkcia neexistuje - bod na grafe je vyrezaný. Ale čím bližšie k hodnote, tým bližšie je funkcia. To je to, čo je cieľom.

Toto pravidlo môžete navyše skontrolovať pomocou kalkulačky. Áno, áno, nehanbite sa, vezmite si kalkulačku, ešte nie sme na Jednotnej štátnej skúške.

Tak skúsme: ;

Nezabudnite si prepnúť kalkulačku do režimu Radians!

atď. Vidíme, že čím menej, tým bližšia hodnota vzťah k

a) Zvážte funkciu. Ako obvykle, nájdime jeho prírastok:

Premeňme rozdiel sínusov na produkt. Na tento účel používame vzorec (zapamätajte si tému „“): .

Teraz derivát:

Urobme náhradu: . Potom pre nekonečne malé je tiež nekonečne malé: . Výraz pre má tvar:

A teraz si to pamätáme s výrazom. A tiež, čo ak možno v súčte (teda at) zanedbať nekonečne malé množstvo.

Takže dostaneme ďalšie pravidlo:derivácia sínusu sa rovná kosínusu:

Ide o základné („tabuľkové“) deriváty. Tu sú v jednom zozname:

Neskôr k nim pridáme niekoľko ďalších, no tieto sú najdôležitejšie, keďže sa používajú najčastejšie.

Cvičenie:

Nájdite deriváciu funkcie v bode;
Nájdite deriváciu funkcie.

Riešenia:

Najprv nájdime derivát vo všeobecnej forme a potom dosaďte jeho hodnotu:
;
.
Tu máme niečo podobné výkonová funkcia. Skúsme ju priviesť
normálne vyzerajúce:
.
Skvelé, teraz môžete použiť vzorec:
.
.
. Eeeeee.... Čo je toto????

Dobre, máte pravdu, zatiaľ nevieme, ako takéto deriváty nájsť. Tu máme kombináciu niekoľkých typov funkcií. Ak chcete s nimi pracovať, musíte sa naučiť niekoľko ďalších pravidiel:

Exponent a prirodzený logaritmus.

V matematike existuje funkcia, ktorej derivácia pre ľubovoľnú hodnotu sa zároveň rovná hodnote samotnej funkcie. Nazýva sa „exponent“ a je to exponenciálna funkcia

Základom tejto funkcie je konštanta – je nekonečná desiatkový, teda iracionálne číslo (ako napr.). Nazýva sa „Eulerovo číslo“, a preto je označené písmenom.

Takže, pravidlo:

Veľmi ľahko zapamätateľné.

No nechoďme ďaleko, pozrime sa na to hneď inverzná funkcia. Ktorá funkcia je inverzná exponenciálna funkcia? Logaritmus:

V našom prípade je základom číslo:

Takýto logaritmus (to znamená logaritmus so základom) sa nazýva „prirodzený“ a používame preň špeciálny zápis: namiesto toho píšeme.

Čomu sa to rovná? Samozrejme, .

Derivácia prirodzeného logaritmu je tiež veľmi jednoduchá:

Príklady:

Nájdite deriváciu funkcie.
Aká je derivácia funkcie?

Odpovede: Vystavovateľ a prirodzený logaritmus- funkcie sú z hľadiska derivácií jedinečne jednoduché. Exponenciálne a logaritmické funkcie s akoukoľvek inou bázou budú mať inú deriváciu, ktorú budeme analyzovať neskôr, keď si prejdeme pravidlá diferenciácie.

Pravidlá diferenciácie

Pravidlá čoho? Opäť nový termín, opäť?!...

Diferenciácia je proces hľadania derivátu.

To je všetko. Ako inak môžete nazvať tento proces jedným slovom? Nie derivácia... Matematici nazývajú diferenciál rovnakým prírastkom funkcie at. Tento výraz pochádza z latinského differentia – rozdiel. Tu.

Pri odvodzovaní všetkých týchto pravidiel použijeme dve funkcie, napríklad a. Budeme tiež potrebovať vzorce pre ich prírastky:

Celkovo existuje 5 pravidiel.

Konštanta je vyňatá z derivačného znamienka.

Ak - nejaké konštantné číslo (konštanta), potom.

Je zrejmé, že toto pravidlo funguje aj pre rozdiel: .

Poďme to dokázať. Nech je to tak, alebo jednoduchšie.

Príklady.

Nájdite derivácie funkcií:

v bode;
v bode;
v bode;
v bode.

Riešenia:

(derivát je vo všetkých bodoch rovnaký, pretože toto lineárna funkcia, pamätáš?);

Derivát produktu

Všetko je tu podobné: vstúpme Nová funkcia a nájdite jeho prírastok:

odvodený:

Príklady:

Nájdite derivácie funkcií a;
Nájdite deriváciu funkcie v bode.

Riešenia:

Derivácia exponenciálnej funkcie

Teraz sú vaše znalosti dostatočné na to, aby ste sa naučili nájsť deriváciu akejkoľvek exponenciálnej funkcie, a nielen exponentov (zabudli ste, čo to je?).

Takže, kde je nejaké číslo.

Deriváciu funkcie už poznáme, takže skúsme našu funkciu zredukovať na nový základ:

Na to použijeme jednoduché pravidlo: . potom:

No podarilo sa. Teraz skúste nájsť deriváciu a nezabudnite, že táto funkcia je zložitá.

Stalo?

Tu sa presvedčte:

Ukázalo sa, že vzorec je veľmi podobný derivátu exponentu: ako to bolo, zostáva rovnaký, objavil sa iba faktor, ktorý je len číslom, ale nie premennou.

Príklady:
Nájdite derivácie funkcií:

Odpovede:

Toto je len číslo, ktoré sa bez kalkulačky nedá vypočítať, teda už sa nedá zapísať v jednoduchej forme. Preto ho v odpovedi necháme v tejto podobe.

Derivácia logaritmickej funkcie

Tu je to podobné: deriváciu prirodzeného logaritmu už poznáte:

Preto nájsť ľubovoľný logaritmus s inou základňou, napríklad:

Tento logaritmus musíme zredukovať na základňu. Ako zmeníte základ logaritmu? Dúfam, že si pamätáte tento vzorec:

Len teraz namiesto toho napíšeme:

Menovateľ je jednoducho konštanta (konštantné číslo, bez premennej). Derivát sa získa veľmi jednoducho:

Deriváty exponenciálnych a logaritmických funkcií sa v jednotnej štátnej skúške takmer nikdy nenachádzajú, ale nebude zbytočné ich poznať.

Derivácia komplexnej funkcie.

Čo sa stalo " komplexná funkcia"? Nie, toto nie je logaritmus ani arkustangens. Tieto funkcie môžu byť ťažko pochopiteľné (hoci ak sa vám zdá logaritmus ťažký, prečítajte si tému „Logaritmy“ a budete v poriadku), ale z matematického hľadiska slovo „komplexný“ neznamená „ťažký“.

Predstavte si malý dopravný pás: dvaja ľudia sedia a robia nejaké akcie s nejakými predmetmi. Napríklad prvý zabalí čokoládovú tyčinku do obalu a druhý ju previaže stuhou. Výsledkom je zložený objekt: čokoládová tyčinka zabalená a previazaná stuhou. Ak chcete zjesť čokoládovú tyčinku, musíte vykonať opačné kroky v opačnom poradí.

Vytvorme podobný matematický reťazec: najprv nájdeme kosínus čísla a potom odmocnime výsledné číslo. Takže dostaneme číslo (čokoláda), nájdem jeho kosínus (obal) a potom utvoríte štvorec, čo som dostal (previažte to stuhou). Čo sa stalo? Funkcia. Toto je príklad komplexnej funkcie: keď na zistenie jej hodnoty vykonáme prvú akciu priamo s premennou a potom druhú akciu s tým, čo vyplynulo z prvej.

Rovnaké kroky môžeme jednoducho urobiť v opačnom poradí: najprv to odmocni a ja potom hľadám kosínus výsledného čísla: . Je ľahké uhádnuť, že výsledok bude takmer vždy iný. Dôležitá vlastnosť komplexné funkcie: keď sa zmení poradie akcií, zmení sa funkcia.

Inými slovami, komplexná funkcia je funkcia, ktorej argumentom je iná funkcia: .

Pre prvý príklad, .

Druhý príklad: (to isté). .

Akcia, ktorú urobíme ako posledná, bude zavolaná „vonkajšia“ funkcia, a akcia vykonaná ako prvá - podľa toho „vnútorná“ funkcia(sú to neformálne názvy, používam ich len na vysvetlenie látky jednoduchým jazykom).

Skúste sami určiť, ktorá funkcia je externá a ktorá interná:

Odpovede: Oddelenie vnútorných a vonkajších funkcií je veľmi podobné zmene premenných: napríklad vo funkcii

Akú akciu vykonáme ako prvú? Najprv vypočítame sínus a až potom ho dáme na kocku. To znamená, že ide o vnútornú funkciu, ale vonkajšiu.
A pôvodnou funkciou je ich zloženie: .
Vnútorné: ; vonkajší: .
Vyšetrenie: .
Vnútorné: ; vonkajší: .
Vyšetrenie: .
Vnútorné: ; vonkajší: .
Vyšetrenie: .
Vnútorné: ; vonkajší: .
Vyšetrenie: .

Zmeníme premenné a dostaneme funkciu.

Teraz vyberieme našu čokoládovú tyčinku a budeme hľadať derivát. Postup je vždy opačný: najprv hľadáme deriváciu vonkajšej funkcie, potom výsledok vynásobíme deriváciou vnútornej funkcie. Vo vzťahu k pôvodnému príkladu to vyzerá takto:

Ďalší príklad:

Takže konečne sformulujme oficiálne pravidlo:

Algoritmus na nájdenie derivácie komplexnej funkcie:

Zdá sa to jednoduché, však?

Pozrime sa na príklady:

Riešenia:

1) Interné: ;

Vonkajšie: ;

2) Interné: ;

(Len to teraz neskúšajte odstrihnúť! Spod kosínusu nič nevychádza, pamätáte?)

3) Interné: ;

Vonkajšie: ;

Hneď je jasné, že ide o trojúrovňovú komplexnú funkciu: veď toto je už sama o sebe zložitá funkcia a extrahujeme z nej aj koreň, čiže vykonáme tretiu akciu (čokoládu vložíme do zavinovačkou a so stuhou v kufríku). Nie je však dôvod na strach: túto funkciu budeme stále „rozbaľovať“ v rovnakom poradí ako obvykle: od konca.

To znamená, že najprv diferencujeme koreň, potom kosínus a až potom výraz v zátvorkách. A potom to všetko vynásobíme.

V takýchto prípadoch je vhodné akcie očíslovať. To znamená, predstavme si, čo vieme. V akom poradí vykonáme akcie na výpočet hodnoty tohto výrazu? Pozrime sa na príklad:

Čím neskôr sa akcia vykoná, tým „externejšia“ bude príslušná funkcia. Postupnosť akcií je rovnaká ako predtým:

Tu je hniezdenie vo všeobecnosti 4-úrovňové. Stanovme si postup.

1. Radikálny výraz. .

2. Koreň. .

3. Sínus. .

4. Štvorec. .

5. Daj to všetko dokopy:

DERIVÁT. STRUČNE O HLAVNÝCH VECIACH

Derivácia funkcie- pomer prírastku funkcie k prírastku argumentu pre nekonečne malý prírastok argumentu:

Základné deriváty:

Pravidlá rozlišovania:

Konštanta je vyňatá z derivačného znamienka:

Derivát súčtu:

Derivát produktu:

Derivát kvocientu:

Derivácia komplexnej funkcie:

Algoritmus na nájdenie derivácie komplexnej funkcie:

Definujeme „internú“ funkciu a nájdeme jej deriváciu.
Definujeme „vonkajšiu“ funkciu a nájdeme jej deriváciu.
Výsledky prvého a druhého bodu vynásobíme.

No, téma je ukončená. Ak čítate tieto riadky, znamená to, že ste veľmi cool.

Pretože len 5% ľudí je schopných niečo zvládnuť sami. A ak dočítate až do konca, tak ste v týchto 5%!

Teraz to najdôležitejšie.

Pochopili ste teóriu na túto tému. A opakujem, toto... toto je proste super! Už teraz ste lepší ako drvivá väčšina vašich rovesníkov.

Problém je, že to nemusí stačiť...

Prečo?

Pre úspešné ukončenie Jednotná štátna skúška na prijatie na vysokú školu s obmedzeným rozpočtom a HLAVNE na celý život.

nebudem ta o nicom presviedcat, poviem len jedno...

Ľudia, ktorí dostali dobré vzdelanie, zarábajú oveľa viac ako tí, ktorí ho nedostali. Toto je štatistika.

Ale to nie je to hlavné.

Hlavne, že sú ŠŤASTNEJŠÍ (existujú také štúdie). Možno preto, že sa pred nimi otvára oveľa viac príležitostí a život sa stáva jasnejším? neviem...

Ale zamysli sa nad sebou...

Čo je potrebné na to, aby ste boli na jednotnej štátnej skúške lepší ako ostatní a nakoniec boli... šťastnejší?

ZÍSKAJTE SI RUKU RIEŠENÍM PROBLÉMOV V TEJTO TÉME.

Na skúške od vás nebudú žiadať teóriu.

Budete potrebovať riešiť problémy s časom.

A ak ste ich nevyriešili (VEĽA!), určite niekde urobíte hlúpu chybu alebo jednoducho nebudete mať čas.

Je to ako v športe – treba to veľakrát zopakovať, aby ste vyhrali.

Nájdite kolekciu kdekoľvek chcete, nevyhnutne s riešeniami, podrobná analýza a rozhodni sa, rozhodni sa, rozhodni sa!

Môžete využiť naše úlohy (voliteľné) a my ich, samozrejme, odporúčame.

Aby ste mohli lepšie využívať naše úlohy, musíte pomôcť predĺžiť životnosť učebnice YouClever, ktorú práve čítate.

Ako? Sú dve možnosti:

Odomknite všetky skryté úlohy v tomto článku - 299 rubľov.
Odomknite prístup ku všetkým skrytým úlohám vo všetkých 99 článkoch učebnice - 499 rubľov.

Áno, takýchto článkov máme v našej učebnici 99 a prístup ku všetkým úlohám a všetkým skrytým textom v nich je možné okamžite otvoriť.

Prístup ku všetkým skrytým úlohám je poskytovaný po CELÚ životnosť stránky.

Na záver...

Ak sa vám nepáčia naše úlohy, nájdite si iné. Len neostávajte pri teórii.

„Rozumiem“ a „Viem vyriešiť“ sú úplne odlišné zručnosti. Potrebujete oboje.

Nájdite problémy a riešte ich!

Derivácia funkcie je jednou z ťažkých tém v školské osnovy. Nie každý absolvent odpovie na otázku, čo je derivát.

Tento článok jednoduchým a jasným spôsobom vysvetľuje, čo je derivát a prečo je potrebný.. V prezentácii sa teraz nebudeme snažiť o matematickú prísnosť. Najdôležitejšie je pochopiť význam.

Pripomeňme si definíciu:

Derivácia je rýchlosť zmeny funkcie.

Na obrázku sú znázornené grafy troch funkcií. Ktorá podľa vás rastie rýchlejšie?

Odpoveď je zrejmá - tretia. Má najvyššiu mieru zmeny, teda najväčší derivát.

Tu je ďalší príklad.

Kostya, Grisha a Matvey dostali prácu v rovnakom čase. Pozrime sa, ako sa zmenili ich príjmy v priebehu roka:

Graf zobrazuje všetko naraz, nie? Kostyov príjem sa za šesť mesiacov viac ako zdvojnásobil. A Grishov príjem sa tiež zvýšil, ale len trochu. A Matveyho príjem klesol na nulu. Počiatočné podmienky sú rovnaké, ale rýchlosť zmeny funkcie, tj derivát, - rôzne. Čo sa týka Matveyho, jeho príjmový derivát je vo všeobecnosti negatívny.

Intuitívne ľahko odhadneme rýchlosť zmeny funkcie. Ale ako to urobíme?

V skutočnosti sa pozeráme na to, ako strmo stúpa graf funkcie nahor (alebo nadol). Inými slovami, ako rýchlo sa mení y, keď sa mení x? Je zrejmé, že rovnakú funkciu môže mať v rôznych bodoch iný význam derivát - to znamená, že sa môže meniť rýchlejšie alebo pomalšie.

Derivácia funkcie sa označuje .

Ukážeme vám, ako ho nájsť pomocou grafu.

Bol nakreslený graf nejakej funkcie. Zoberme si bod s osou x. V tomto bode nakreslíme dotyčnicu ku grafu funkcie. Chceme odhadnúť, ako strmo stúpa graf funkcie. Výhodná hodnota pre to je tangens tangens uhla.

Derivácia funkcie v bode sa rovná tangente dotyčnicového uhla nakresleného ku grafu funkcie v tomto bode.

Upozorňujeme, že ako uhol sklonu dotyčnice berieme uhol medzi dotyčnicou a kladným smerom osi.

Niekedy sa študenti pýtajú, čo je dotyčnica ku grafu funkcie. Toto je priamka, ktorá má jeden spoločný bod s grafom v tejto časti a ako je znázornené na našom obrázku. Vyzerá to ako dotyčnica ku kruhu.

Poďme to nájsť. Pamätáme si, že dotyčnica ostrého uhla v pravouhlom trojuholníku sa rovná pomeru protiľahlej strany k susednej strane. Z trojuholníka:

Našli sme deriváciu pomocou grafu bez toho, aby sme poznali vzorec funkcie. Takéto problémy sa často nachádzajú v Jednotnej štátnej skúške z matematiky pod číslom.

Je tu ešte jeden dôležitý vzťah. Pripomeňme, že priamka je daná rovnicou

Množstvo v tejto rovnici sa nazýva sklon priamky. Rovná sa dotyčnici uhla sklonu priamky k osi.

Chápeme to

Zapamätajme si tento vzorec. Vyjadruje geometrický význam derivácie.

Derivácia funkcie v bode sa rovná sklonu dotyčnice nakreslenej ku grafu funkcie v tomto bode.

Inými slovami, derivácia sa rovná dotyčnici dotyčnicového uhla.

Už sme povedali, že tá istá funkcia môže mať v rôznych bodoch rôzne derivácie. Pozrime sa, ako derivácia súvisí so správaním funkcie.

Nakreslíme graf nejakej funkcie. Nechajte túto funkciu v niektorých oblastiach rásť a v iných znižovať a rôznymi rýchlosťami. A nech má táto funkcia maximálny a minimálny počet bodov.

V určitom bode sa funkcia zvýši. Dotyčnica ku grafu nakreslenému v bode tvorí ostrý uhol; s kladným smerom osi. To znamená, že derivácia v bode je kladná.

V tomto bode naša funkcia klesá. Dotyčnica v tomto bode zviera tupý uhol; s kladným smerom osi. Keďže tangens tupého uhla je záporný, derivácia v bode je záporná.

Čo sa stane:

Ak je funkcia rastúca, jej derivácia je kladná.

Ak klesá, jeho derivácia je záporná.

Čo sa stane s maximálnym a minimálnym počtom bodov? Vidíme, že v bodoch (maximálny bod) a (minimálny bod) je dotyčnica vodorovná. Preto je dotyčnica dotyčnice v týchto bodoch nula a derivácia je tiež nulová.

Bod - maximálny bod. V tomto bode je nárast funkcie nahradený poklesom. V dôsledku toho sa znamienko derivácie mení v bode z „plus“ na „mínus“.

V bode - minimálnom bode - je derivácia tiež nulová, ale jej znamienko sa mení z „mínus“ na „plus“.

Záver: pomocou derivácie môžeme zistiť všetko, čo nás o správaní funkcie zaujíma.

Ak je derivácia kladná, funkcia sa zvyšuje.

Ak je derivácia záporná, funkcia klesá.

V maximálnom bode je derivácia nula a mení znamienko z „plus“ na „mínus“.

V minimálnom bode je derivácia tiež nula a mení znamienko z „mínus“ na „plus“.

Zapíšme si tieto závery vo forme tabuľky:

	zvyšuje	maximálny bod	klesá	minimálny bod	zvyšuje
+	0	-	0	+

Urobme dve malé upresnenia. Pri riešení problému budete potrebovať jeden z nich. Ďalší - v prvom ročníku, s vážnejším štúdiom funkcií a derivátov.

Je možné, že derivácia funkcie sa v určitom bode rovná nule, ale funkcia v tomto bode nemá ani maximum, ani minimum. Ide o tzv :

V bode je dotyčnica ku grafu vodorovná a derivácia je nula. Pred bodom sa však funkcia zvýšila - a po bode sa naďalej zvyšuje. Znamienko derivátu sa nemení – zostáva kladné tak, ako bolo.

Stáva sa tiež, že v bode maxima alebo minima derivát neexistuje. Na grafe to zodpovedá prudkému zlomu, keď nie je možné nakresliť dotyčnicu v danom bode.

Ako nájsť deriváciu, ak funkcia nie je daná grafom, ale vzorcom? V tomto prípade platí