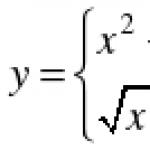Daný graf primitívnej funkcie na zistenie hodnoty funkcie. Antidivatív funkcie. Hlavná vlastnosť primitívneho prostriedku

Typ práce: 7
Téma: Antidivatív funkcie

Stav

Na obrázku je graf funkcie y \u003d f (x) (čo je prerušovaná čiara zložená z troch úsečiek). Pomocou obrázku vypočítajte F (9) -F (5), kde F (x) je jednou z hlavných funkcií f (x).

Zobraziť riešenie

Rozhodnutie

Podľa Newtonovho-Leibnizovho vzorca sa rozdiel F (9) -F (5), kde F (x) je jednou z hlavných funkcií funkcie f (x), rovná ploche krivočarého lichobežníka ohraničeného grafom funkcie y \u003d f (x), priamkami y \u003d 0, x \u003d 9 a x \u003d 5. Podľa grafu určíme, že naznačený zakrivený lichobežník je lichobežník so základňami rovnými 4 a 3 a výškou 3.

Jeho rozloha je \\ frac (4 + 3) (2) \\ cdot 3 \u003d 10,5.

Odpoveď

Typ práce: 7
Téma: Antidivatív funkcie

Stav

Na obrázku je znázornený graf funkcie y \u003d F (x) - jednej z primitívnych funkcií niektorej funkcie f (x), definovanej na intervale (-5; 5). Pomocou obrázka určte počet riešení rovnice f (x) \u003d 0 na segmente [-3; štyri].

Zobraziť riešenie

Rozhodnutie

Podľa definície antiderivátu platí táto rovnosť: F "(x) \u003d f (x). Rovnicu f (x) \u003d 0 preto môžeme zapísať ako F" (x) \u003d 0. Pretože obrázok ukazuje graf funkcie y \u003d F (x), je potrebné nájsť tie body intervalu [-3; 4], v ktorom sa derivácia funkcie F (x) rovná nule. Z obrázku je zrejmé, že pôjde o úsečky krajných bodov (maximálnych alebo minimálnych) grafu F (x). Na uvedenom intervale ich je presne 7 (minimálne štyri body a tri maximálne).

Odpoveď

Zdroj: „Matematika. Príprava na skúšku-2017. Úroveň profilu„. Ed. FF Lysenko, S. Yu. Kulabukhova.

Typ práce: 7
Téma: Antidivatív funkcie

Stav

Na obrázku je graf funkcie y \u003d f (x) (čo je prerušovaná čiara zložená z troch úsečiek). S odvolaním sa na obrázok vypočítajte F (5) -F (0), kde F (x) je jednou z primitívnych funkcií f (x).

Zobraziť riešenie

Rozhodnutie

Podľa Newtonovho-Leibnizovho vzorca sa rozdiel F (5) -F (0), kde F (x) je jednou z hlavných funkcií funkcie f (x), rovná ploche krivočarého lichobežníka ohraničeného grafom funkcie y \u003d f (x), priamkami y \u003d 0, x \u003d 5 a x \u003d 0. Podľa grafu určíme, že indikovaný zakrivený lichobežník je lichobežník so základňami rovnými 5 a 3 a výškou 3.

Jeho rozloha je \\ frac (5 + 3) (2) \\ cdot 3 \u003d 12.

Odpoveď

Zdroj: „Matematika. Príprava na skúšku-2017. Úroveň profilu ". Ed. FF Lysenko, S. Yu. Kulabukhova.

Typ práce: 7
Téma: Antidivatív funkcie

Stav

Na obrázku je znázornený graf funkcie y \u003d F (x) - jednej z primitívnych funkcií niektorej funkcie f (x), definovanej na intervale (-5; 4). Pomocou obrázku určite počet riešení rovnice f (x) \u003d 0 na úsečke (-3; 3].

Zobraziť riešenie

Rozhodnutie

Z obrázku je zrejmé, že pôjde o úsečky krajných bodov (maximálnych alebo minimálnych) grafu F (x). Na uvedenom intervale je ich presne 5 (dva minimálne body a tri maximálne body).

Odpoveď

Zdroj: „Matematika. Príprava na skúšku-2017. Úroveň profilu ". Ed. FF Lysenko, S. Yu. Kulabukhova.

Typ práce: 7
Téma: Antidivatív funkcie

Stav

Na obrázku je graf niektorej funkcie y \u003d f (x). Funkcia F (x) \u003d - x ^ 3 + 4,5x ^ 2-7 je jedným z antiderivátov funkcie f (x).

Nájdite oblasť tieňovaného tvaru.

Zobraziť riešenie

Rozhodnutie

Tieňovaná figúra je krivočiary lichobežník ohraničený zhora grafom funkcie y \u003d f (x), priamok y \u003d 0, x \u003d 1 a x \u003d 3. Podľa Newton-Leibnizovho vzorca sa jeho plocha S rovná rozdielu F (3) -F (1), kde F (x) je primitívom funkcie f (x) uvedenej v podmienke. preto S \u003d F (3) -F (1) \u003d -3 ^ 3 + (4.5) \\ cdot 3 ^ 2 -7 - (- 1 ^ 3 + (4.5) \\ cdot 1 ^ 2-7) \u003d 6,5-(-3,5)= 10.

Odpoveď

Zdroj: „Matematika. Príprava na skúšku-2017. Úroveň profilu ". Ed. FF Lysenko, S. Yu. Kulabukhova.

Typ práce: 7
Téma: Antidivatív funkcie

Stav

Na obrázku je graf niektorej funkcie y \u003d f (x). Funkcia F (x) \u003d x ^ 3 + 6x ^ 2 + 13x-5 je jedným z antiderivátov funkcie f (x). Nájdite oblasť tieňovaného tvaru.

Funkcia F (x ) zavolal primitívne pre funkciu f (x) v danom intervale, ak pre všetkých x z tohto intervalu rovnosť

F “(x ) = f(x ) .

Napríklad funkcia F (x) \u003d x 2 f (x ) = 2x , pretože

F "(x) \u003d (x 2 )" = 2x \u003d f (x). ◄

Hlavná vlastnosť primitívneho prostriedku

Ak F (x) - primitívne pre funkciu f (x) v danom intervale, potom funkcia f (x) má nekonečne veľa primitívnych látok a všetky tieto primitívne látky možno napísať ako F (x) + C.kde ZO Je ľubovoľná konštanta.

Napríklad

Funkcia F (x) \u003d x 2 + 1 je primitívom funkcie

f (x ) = 2x , pretože F "(x) \u003d (x 2 + 1 )" = 2 x \u003d f (x);

funkcia F (x) \u003d x 2 - 1 je primitívom funkcie

f (x ) = 2x , pretože F "(x) \u003d (x 2 - 1)" = 2x \u003d f (x) ;

funkcia F (x) \u003d x 2 - 3 je primitívom funkcie

f (x) = 2x , pretože F "(x) \u003d (x 2 - 3)" = 2 x \u003d f (x);

ľubovoľná funkcia F (x) \u003d x 2 + ZO kde ZO - ľubovoľná konštanta a iba takáto funkcia je pre funkciu primitívnym f (x) = 2x . ◄

Pravidlá výpočtu antidumpingových opatrení

Ak F (x) - primitívne pre f (x) a G (x) - primitívne pre g (x) potom F (x) + G (x) - primitívne pre f (x) + g (x) ... Inými slovami, primitívum súčtu sa rovná súčtu primitívov .
Ak F (x) - primitívne pre f (x) a k - teda konštantná k · F (x) - primitívne pre k · f (x) ... Inými slovami, konštantný faktor je možné posunúť mimo znamienka derivácie .
Ak F (x) - primitívne pre f (x) a k, b- trvalé a k ≠ 0 potom 1 / k F (k x +b ) - primitívne pre f(k x + b) .

Neurčitý integrál

Nie určitý integrál z funkcie f (x) nazývaný výraz F (x) + C., teda súhrn všetkých antiderivatív danej funkcie f (x) ... Neurčitý integrál sa označuje takto:

∫ f (x) dx \u003d F (x) + С. ,

f (x)- hovor integrand ;

f (x) dx - hovor integrand ;

x - hovor premenná integrácie ;

F (x) - jeden z vedľajších účinkov funkcie f (x) ;

ZO Je ľubovoľná konštanta.

Napríklad ∫ 2 x dx \u003dx 2 + ZO , ∫ cosx dx \u003dhriech x + ZO atď. ◄

Slovo „integrál“ pochádza z latinského slova celé číslo čo znamená „obnovený“. Vzhľadom na neurčitý integrál z 2 x , nejako obnovíme funkciu x 2 ktorého derivát sa rovná 2 x ... Rekonštrukcia funkcie z jej derivácie, alebo, ktorá je rovnaká, nájdenie neurčitého integrálu nad daným integrandom, sa nazýva integračný tejto funkcie. Integrácia je inverzná operácia diferenciácie. Na overenie správnosti integrácie stačí odlíšiť výsledok a získať funkciu integrand.

Základné vlastnosti neurčitého integrálu

Derivát neurčitého integrálu sa rovná celému číslu:

(∫ f (x) dx )" \u003d f (x) .

Konštantný faktor celého čísla možno vziať mimo integrálneho znamienka:

∫ k · f (x) dx = k · ∫ f (x) dx .

Integrál súčtu (rozdielu) funkcií rovná sa súčtu (rozdiel) integrálov týchto funkcií:

∫ ( f (x) ± g (x ) ) dx = ∫ f (x) dx ± ∫ g (x ) dx .

Ak k, b- trvalé a k ≠ 0 potom

∫ f ( k x + b) dx = 1 / k F (k x +b ) + C. .

Tabuľka protikladných a neurčitých integrálov

	f (x)	F (x) + C.	∫ f (x) dx \u003d F (x) + С.
I.	$$0$$	$$ C $$	$$ \\ int 0dx \u003d C $$
II.	$$ k $$	$$ kx + C $$	$$ \\ int kdx \u003d kx + C $$
III.	$$ x ^ n ~ (n \\ neq-1) $$	$$ \\ frac (x ^ (n + 1)) (n + 1) + C $$	$$ \\ int x ^ ndx \u003d \\ frac (x ^ (n + 1)) (n + 1) + C $$
IV.	$$ \\ frac (1) (x) $$	$$ \\ ln \| x \| + C $$	$$ \\ int \\ frac (dx) (x) \u003d \\ ln \| x \| + C $$
V.	$$ \\ sin x $$	$$ - \\ cos x + C $$	$$ \\ int \\ sin x ~ dx \u003d - \\ cos x + C $$
Vi.	$$ \\ cos x $$	$$ \\ sin x + C $$	$$ \\ int \\ cos x ~ dx \u003d \\ sin x + C $$
VII.	$$ \\ frac (1) (\\ cos ^ 2x) $$	$$ \\ textrm (tg) ~ x + C $$	$$ \\ int \\ frac (dx) (\\ cos ^ 2x) \u003d \\ textrm (tg) ~ x + C $$
VIII.	$$ \\ frac (1) (\\ sin ^ 2x) $$	$$ - \\ textrm (ctg) ~ x + C $$	$$ \\ int \\ frac (dx) (\\ sin ^ 2x) \u003d - \\ textrm (ctg) ~ x + C $$
IX.	$$ e ^ x $$	$$ e ^ x + C $$	$$ \\ int e ^ xdx \u003d e ^ x + C $$
X.	$$ a ^ x $$	$$ \\ frac (a ^ x) (\\ ln a) + C $$	$$ \\ int a ^ xdx \u003d \\ frac (a ^ x) (\\ ln a) + C $$
XI.	$$ \\ frac (1) (\\ sqrt (1-x ^ 2)) $$	$$ \\ arcsin x + C $$	$$ \\ int \\ frac (dx) (\\ sqrt (1-x ^ 2)) \u003d \\ arcsin x + C $$
XII.	$$ \\ frac (1) (\\ sqrt (a ^ 2-x ^ 2)) $$	$$ \\ arcsin \\ frac (x) (a) + C $$	$$ \\ int \\ frac (dx) (\\ sqrt (a ^ 2-x ^ 2)) \u003d \\ arcsin \\ frac (x) (a) + C $$
XIII.	$$ \\ frac (1) (1 + x ^ 2) $$	$$ \\ textrm (arctg) ~ x + C $$	$$ \\ int \\ frac (dx) (1 + x ^ 2) \u003d \\ textrm (arctg) ~ x + C $$
XIV.	$$ \\ frac (1) (a ^ 2 + x ^ 2) $$	$$ \\ frac (1) (a) \\ textrm (arctg) ~ \\ frac (x) (a) + C $$	$$ \\ int \\ frac (dx) (a ^ 2 + x ^ 2) \u003d \\ frac (1) (a) \\ textrm (arctg) ~ \\ frac (x) (a) + C $$
XV.	$$ \\ frac (1) (\\ sqrt (a ^ 2 + x ^ 2)) $$	$$ \\ ln \| x + \\ sqrt (a ^ 2 + x ^ 2) \| + C $$	$$ \\ int \\ frac (dx) (\\ sqrt (a ^ 2 + x ^ 2)) \u003d \\ ln \| x + \\ sqrt (a ^ 2 + x ^ 2) \| + C $$
XVI.	$$ \\ frac (1) (x ^ 2-a ^ 2) ~ (a \\ neq0) $$	$$ \\ frac (1) (2a) \\ ln \\ begin (vmatrix) \\ frac (x-a) (x + a) \\ end (vmatrix) + C $$	$$ \\ int \\ frac (dx) (x ^ 2-a ^ 2) \u003d \\ frac (1) (2a) \\ ln \\ begin (vmatrix) \\ frac (xa) (x + a) \\ end (vmatrix) + C $$
XVII.	$$ \\ textrm (tg) ~ x $$	$$ - \\ ln \| \\ cos x \| + C $$	$$ \\ int \\ textrm (tg) ~ x ~ dx \u003d - \\ ln \| \\ cos x \| + C $$
XVIII.	$$ \\ textrm (ctg) ~ x $$	$$ \\ ln \| \\ sin x \| + C $$	$$ \\ int \\ textrm (ctg) ~ x ~ dx \u003d \\ ln \| \\ sin x \| + C $$
XIX.	$$ \\ frac (1) (\\ sin x) $$	$$ \\ ln \\ begin (vmatrix) \\ textrm (tg) ~ \\ frac (x) (2) \\ end (vmatrix) + C $$	$$ \\ int \\ frac (dx) (\\ sin x) \u003d \\ ln \\ begin (vmatrix) \\ textrm (tg) ~ \\ frac (x) (2) \\ end (vmatrix) + C $$
XX.	$$ \\ frac (1) (\\ cos x) $$	$$ \\ ln \\ begin (vmatrix) \\ textrm (tg) \\ left (\\ frac (x) (2) + \\ frac (\\ pi) (4) \\ right) \\ end (vmatrix) + C $$	$$ \\ int \\ frac (dx) (\\ cos x) \u003d \\ ln \\ begin (vmatrix) \\ textrm (tg) \\ left (\\ frac (x) (2) + \\ frac (\\ pi) (4) \\ right ) \\ end (vmatrix) + C $$
Antideriváty a neurčité integrály uvedené v tejto tabuľke sa zvyčajne nazývajú tabuľkové primitívne látky a tabuľkové integrály .

Určite integrál

Nechajte v intervale [a; b] daný spojitá funkcia y \u003d f (x) potom určitý integrál od a do b funkcia f (x) sa nazýva prírastok antiderivátu F (x) táto funkcia, to znamená

$$ \\ int_ (a) ^ (b) f (x) dx \u003d F (x) | (_a ^ b) \u003d ~~ F (a) -F (b). $$

Čísla aa b podľa toho pomenované nižšie a hore limity integrácie.

Základné pravidlá pre výpočet určitého integrálu

1. \\ (\\ int_ (a) ^ (a) f (x) dx \u003d 0 \\);

2. \\ (\\ int_ (a) ^ (b) f (x) dx \u003d - \\ int_ (b) ^ (a) f (x) dx \\);

3. \\ (\\ int_ (a) ^ (b) kf (x) dx \u003d k \\ int_ (a) ^ (b) f (x) dx, \\) kde k - konštantný;

4. \\ (\\ int_ (a) ^ (b) (f (x) ± g (x)) dx \u003d \\ int_ (a) ^ (b) f (x) dx ± \\ int_ (a) ^ (b) g (x) dx \\);

5. \\ (\\ int_ (a) ^ (b) f (x) dx \u003d \\ int_ (a) ^ (c) f (x) dx + \\ int_ (c) ^ (b) f (x) dx \\) ;

6. \\ (\\ int _ (- a) ^ (a) f (x) dx \u003d 2 \\ int_ (0) ^ (a) f (x) dx \\), kde f (x) - rovnomerná funkcia;

7. \\ (\\ int _ (- a) ^ (a) f (x) dx \u003d 0 \\), kde f (x) Je nepárna funkcia.

Komentovať ... Vo všetkých prípadoch sa predpokladá, že celé čísla sú integrovateľné v číselných intervaloch, ktorých hranice sú limitmi integrácie.

Geometrický a fyzikálny význam určitého integrálu

Geometrický význam určitý integrál	Fyzický zmysel určitý integrál

Námestie S krivočiary lichobežník (údaj ohraničený grafom spojitého pozitívu v intervale) [a; b] funkcia f (x) , os Vôl a priame x \u003d a , x \u003d b ) sa počíta podľa vzorca $$ S \u003d \\ int_ (a) ^ (b) f (x) dx. $$	Spôsob s, ktorý hmotný bod prekonal, pohybujúci sa po priamke rýchlosťou meniacou sa podľa zákona v (t) , pre časový interval a ; b], potom oblasť obrázku, obmedzená grafmi týchto funkcií a priamkami x \u003d a , x \u003d b , vypočítané podľa vzorca $$ S \u003d \\ int_ (a) ^ (b) (f (x) -g (x)) dx. $$
	Napríklad Vypočítame plochu figúry ohraničenú čiarami y \u003d x 2 a y \u003d2 - X . Poďme si schematicky zobraziť grafy týchto funkcií a zvýrazniť inou farbou obrázok, ktorého oblasť sa nachádza. Aby sme našli limity integrácie, riešime rovnicu: x 2 = 2 - X ; x 2 + X -2 = 0 ; x 1 = -2, X 2 = 1 . $$ S \u003d \\ int _ (- 2) ^ (1) ((2-x) -x ^ 2) dx \u003d $$
$$ \u003d \\ int _ (- 2) ^ (1) (2-xx ^ 2) dx \u003d \\ vľavo (2x- \\ frac (x ^ 2) (2) - \\ frac (x ^ 3) (2) \\ vpravo) \\ bigm \| (_ (- 2) ^ (~ 1)) \u003d 4 \\ frac (1) (2). $$ ◄

Objem tela revolúcie

Ak je telo získané v dôsledku otáčania okolo osi Vôl krivočiary lichobežník ohraničený grafom spojitého a nezáporného v intervale [a; b] funkcia y \u003d f (x) a priame x \u003d aa x \u003d b potom sa to volá orgán revolúcie .

Objem rotačného telesa sa vypočíta podľa vzorca

$$ V \u003d \\ pi \\ int_ (a) ^ (b) f ^ 2 (x) dx. $$

Ak sa rotačné teliesko získa v dôsledku rotácie obrazca ohraničeného zhora a zdola grafmi funkcií y \u003d f (x) a y \u003d g (x) , v uvedenom poradí

$$ V \u003d \\ pi \\ int_ (a) ^ (b) (f ^ 2 (x) -g ^ 2 (x)) dx. $$

Napríklad Vypočítame objem kužeľa s polomerom r a výšky h .

Umiestnite kužeľ do obdĺžnikového súradnicového systému tak, aby sa jeho os zhodovala s osou Vôl , a stred podstavca bol pri začiatku. Rotácia generátora AB definuje kužeľ. Od rovnice AB

$$ \\ frac (x) (h) + \\ frac (y) (r) \u003d 1, $$

$$ y \u003d r- \\ frac (rx) (h) $$

a pre objem kužeľa, ktorý máme

$$ V \u003d \\ pi \\ int_ (0) ^ (h) (r- \\ frac (rx) (h)) ^ 2dx \u003d \\ pi r ^ 2 \\ int_ (0) ^ (h) (1- \\ frac ( x) (h)) ^ 2dx \u003d - \\ pi r ^ 2h \\ cdot \\ frac ((1- \\ frac (x) (h)) ^ 3) (3) | (_0 ^ h) \u003d - \\ pi r ^ 2 h \\ doľava (0- \\ frac (1) (3) \\ doprava) \u003d \\ frac (\\ pi r ^ 2h) (3). $$

◄

Účel:

Formovanie konceptu primitívne.
Príprava na vnímanie integrálu.
Budovanie výpočtových schopností.
Podpora pocitu krásy (schopnosť vidieť krásu neobvykle).

Matematická analýza je súbor častí matematiky venovaných štúdiu funkcií a ich zovšeobecňovaniu metódami diferenciálneho a integrálneho počtu.

Doteraz sme študovali časť matematickej analýzy zvanú diferenciálny počet, ktorej podstatou je štúdium funkcií v „malom“.

Tých. vyšetrovanie funkcie v dostatočne malých štvrtiach každého bodu definície. Jednou z operácií diferenciácie je nájdenie derivácie (diferenciálu) a jej použitie pri štúdiu funkcií.

Nemenej dôležitý je inverzný problém. Ak je známe správanie sa funkcie v blízkosti každého bodu jej definície, ako je možné obnoviť funkciu ako celok, t.j. v celej oblasti jeho vymedzenia. Tento problém je predmetom štúdia takzvaného integrálneho počtu.

Integrácia je činnosť inverzná k diferenciácii. Alebo obnovenie funkcie f (x) z danej derivácie f` (x). Latinské slovo „Integro“ znamená reštaurovanie.

Príklad č.

Nech (x) `\u003d 3x 2.
Nájdite f (x).

Rozhodnutie:

Na základe pravidla diferenciácie je ľahké uhádnuť, že f (x) \u003d x 3, pretože (x 3) `\u003d 3x 2
Je však ľahké vidieť, že f (x) sa nachádza nejednoznačne.
Ako f (x) môžeme brať
f (x) \u003d x 3 +1
f (x) \u003d x 3 +2
f (x) \u003d x 3 -3 atď.

Pretože derivát každého z nich je 3x 2. (Derivácia konštanty je 0). Všetky tieto funkcie sa navzájom konštantne líšia. Preto môžeme všeobecné riešenie úlohy napísať v tvare f (x) \u003d x 3 + C, kde C predstavuje akékoľvek konštantné reálne číslo.

Zavolá sa ktorákoľvek z nájdených funkcií f (x) PRIMÁRNY pre funkciu F` (x) \u003d 3x 2

Definícia. Funkcia F (x) sa nazýva primitívna pre funkciu f (x) v danom intervale J, ak pre všetky x z tohto intervalu F` (x) \u003d f (x). Funkcia F (x) \u003d x 3 je teda primitívom pre f (x) \u003d 3x 2 na (- ∞; ∞).
Pretože pre všetky x ~ R platí rovnosť: F` (x) \u003d (x 3) `\u003d 3x 2

Ako sme už poznamenali, táto funkcia má nekonečné množstvo primitívnych látok (pozri príklad č. 1).

Príklad č. Funkcia F (x) \u003d x je primitívna pre všetky f (x) \u003d 1 / x na intervale (0; +), pretože pre všetky x z tohto intervalu platí rovnosť.
F` (x) \u003d (x 1/2) `\u003d 1 / 2x -1/2 \u003d 1 / 2x

Príklad č. Funkcia F (x) \u003d tg3x je primitívom pre f (x) \u003d 3 / cos3x na intervale (-n / 2; P / 2),
odkedy F` (x) \u003d (tg3x) `\u003d 3 / cos 2 3x

Príklad č. Funkcia F (x) \u003d 3sin4x + 1 / x-2 primitívne pre f (x) \u003d 12cos4x-1 / x 2 na intervale (0; ∞)
odkedy F` (x) \u003d (3sin4x) + 1 / x-2) \u003d 4cos4x-1 / x 2

Prednáška 2.

Téma: Antiderivatívum. Hlavná vlastnosť antiiderivatívnej funkcie.

Pri štúdiu antiderivátu sa budeme opierať o nasledujúce tvrdenie. Kritérium pre stálosť funkcie: Ak je na intervale J derivácia Ψ (x) funkcie rovná 0, potom je v tomto intervale funkcia Ψ (x) konštantná.

Toto tvrdenie možno demonštrovať geometricky.

Je známe, že Ψ` (x) \u003d tanα, γde α-uhol sklonu dotyčnice ku grafu funkcie Ψ (x) v bode s úsečkou x 0. Ak Ψ` (υ) \u003d 0 v ktoromkoľvek bode intervalu J, potom tanα \u003d 0 δ pre každú dotyčnicu ku grafu funkcie Ψ (x). To znamená, že dotyčnica grafu funkcie v ktoromkoľvek bode je rovnobežná s osou úsečky. Preto sa v uvedenom intervale graf funkcie Ψ (x) zhoduje so segmentom priamky y \u003d C.

Funkcia f (x) \u003d c je teda konštantná v intervale J, ak f` (x) \u003d 0 v tomto intervale.

V skutočnosti pre ľubovoľné х 1 a х 2 z intervalu J, pomocou vety o strednej hodnote funkcie, môžeme napísať:
f (x 2) - f (x 1) \u003d f` (c) (x 2 - x 1), pretože f` (c) \u003d 0, potom f (x 2) \u003d f (x 1)

Veta: (Hlavná vlastnosť antiiderivatívnej funkcie)

Ak je F (x) jedným z primitívnych činiteľov pre funkciu f (x) na intervale J, potom má množina všetkých primitívnych premenných tejto funkcie tvar: F (x) + С, kde С je akékoľvek skutočné číslo.

Dôkazy:

Nech F` (x) \u003d f (x), potom (F (x) + C) `\u003d F` (x) + C` \u003d f (x), pre x Є J.
Predpokladajme, že na intervale J je Φ (x) - ďalšie primitívne pre f (x), t.j. Φ` (x) \u003d f (x),
potom (Φ (x) - F (x)) `\u003d f (x) - f (x) \u003d 0, pre x Є J.
To znamená, že Φ (x) - F (x) je na intervale J konštantná.
Preto Φ (x) - F (x) \u003d C.
Odkiaľ Φ (x) \u003d F (x) + C.
To znamená, že ak F (x) je primitívom pre funkciu f (x) na intervale J, potom má množina všetkých primitívov tejto funkcie tvar: F (x) + C, kde C je akékoľvek reálne číslo.
Preto sa akékoľvek dve primitívne funkcie danej funkcie líšia od seba konštantným výrazom.

Príklad: Nájdite množinu primitívnych funkcií funkcie f (x) \u003d cos x. Zobraziť grafy prvých troch.

Rozhodnutie: Sin x - jedno z primitívnych činiteľov pre funkciu f (x) \u003d cos x
F (x) \u003d Sin x + C je množina všetkých primitívnych látok.

F 1 (x) \u003d Sin x-1
F 2 (x) \u003d Sin x
F 3 (x) \u003d Sin x + 1

Geometrické znázornenie: Graf ľubovoľného primitívu F (x) + C možno získať z grafu primitívne F (x) pomocou paralelného prekladu r (0; c).

Príklad: Pre funkciu f (x) \u003d 2x nájdite deriváciu, ktorej graf prechádza bodom M (1; 4)

Rozhodnutie: F (x) \u003d x 2 + C je množina všetkých primitívnych látok, F (1) \u003d 4 - vyjadrením problému.
Preto 4 \u003d 1 2 + C
C \u003d 3
F (x) \u003d x 2 +3

Antiderivatívna funkcia f (x) medzi (a; b) takáto funkcia sa volá F (x)že rovnosť platí pre každého x z daného intervalu.

S prihliadnutím na skutočnosť, že derivácia konštanty ZO sa rovná nule, potom je rovnosť pravdivá. Takže funkcia f (x) má veľa primitívnych látok F (x) + C., pre ľubovoľnú konštantu ZO, a tieto primitívne látky sa navzájom líšia ľubovoľnou konštantnou hodnotou.

Definícia neurčitý integrál.

Celá sada protichodných látok f (x) sa nazýva neurčitý integrál tejto funkcie a označuje sa .

Výraz sa volá integranda f (x) – integrand... Celé číslo je rozdiel funkcie f (x).

Akcia hľadania neznámej funkcie pre daný diferenciál sa volá neistý integrácia, pretože výsledkom integrácie je viac ako jedna funkcia F (x)a mnoho z jeho anti-negatívnych látok F (x) + C..

Geometrický význam neurčitého integrálu. Graf antiderivátu D (x) sa nazýva integrálna krivka. V súradnicovom systéme x0y grafy všetkých primitívnych funkcií danej funkcie predstavujú rodinu kriviek, ktoré závisia od hodnoty konštanty C a sú navzájom získavané paralelným posunom pozdĺž osi 0y. V príklade diskutovanom vyššie máme:

J 2 x ^ x \u003d x2 + C.

Rodina antiderivátov (x + C) je geometricky interpretovaná ako súbor paraboly.

Ak je potrebné nájsť jednu z rodiny primitívnych látok, potom sa stanovia ďalšie podmienky na určenie konštanty C. Zvyčajne sa na tento účel nastavia počiatočné podmienky: pre hodnotu argumentu x \u003d x0 má funkcia hodnotu D (x0) \u003d y0.

Príklad. Je potrebné nájsť to z anti-negatívnych funkcií funkcie y \u003d 2 x, ktorá má hodnotu 3 pri x0 \u003d 1.

Požadované primitívne: D (x) \u003d x2 + 2.

Rozhodnutie. ^ 2x ^ x \u003d x2 + C; 12 + C \u003d 3; C \u003d 2.

2. Základné vlastnosti neurčitého integrálu

1. Derivát neurčitého integrálu sa rovná celému číslu:

2. Diferenciál neurčitého integrálu sa rovná celému číslu:

3. Neurčitý integrál diferenciálu niektorej funkcie sa rovná súčtu tejto funkcie a ľubovoľnej konštante:

4. Konštantný faktor možno vylúčiť z integrálneho znamienka:

5. Integrál súčtu (rozdielu) sa rovná súčtu (rozdielu) integrálov:

6. Táto nehnuteľnosť je kombináciou nehnuteľností 4 a 5:

7. Vlastnosť invariantnosti neurčitého integrálu:

Ak potom

8. Majetok:

Ak potom

V skutočnosti je táto vlastnosť špeciálnym prípadom integrácie pomocou metódy zmeny premennej, ktorej sa podrobnejšie venujeme v nasledujúcej časti.

Uvažujme príklad:

3. Integračná metóda, v ktorom je tento integrál redukovaný na jeden alebo viac tabuľkových integrálov identickými transformáciami integrandu (alebo výrazu) a uplatnením vlastností neurčitého integrálu, sa nazýva priama integrácia... Pri redukcii tohto integrálu na integrál tabuľky sa často používajú nasledujúce transformácie diferenciálu (operácia „ znak diferenciálu»):

Spravidla f '(u) du \u003d d (f (u)). toto (vzorec sa veľmi často používa pri výpočte integrálov.

Nájdite integrál

Rozhodnutie. Použijeme vlastnosti integrálu a zmenšíme tento integrál na niekoľko tabuľkových.

4. Integrácia substitučnou metódou.

Podstata metódy je v tom, že zavedieme novú premennú, vyjadríme cez ňu celú premennú, čím sa dostaneme k tabuľkovej (alebo jednoduchšej) podobe integrálu.

Substitučná metóda veľmi často pomáha pri integrácii trigonometrických funkcií a funkcií s radikálmi.

Príklad.

Nájdite neurčitý integrál .

Rozhodnutie.

Poďme predstaviť novú premennú. Poďme sa vyjadriť x naprieč z:

Získané výrazy dosadíme do pôvodného integrálu:

Z tabuľky primitívnych liekov, ktoré máme .

Zostáva vrátiť sa k pôvodnej premennej x:

Odpoveď:

Jednou z operácií diferenciácie je nájdenie derivácie (diferenciálu) a jej použitie pri štúdiu funkcií.

Integrácia je činnosť inverzná k diferenciácii. Alebo obnovenie funkcie f (x) z danej derivácie f` (x). Latinské slovo „integro“ znamená reštaurovanie.

Príklad č.

Nech (f (x)) ‘\u003d 3x 2. Nájdite f (x).

Rozhodnutie:

Na základe pravidla diferenciácie je ľahké uhádnuť, že f (x) \u003d x 3, pretože

(x 3) '\u003d 3x 2 Je však ľahké si všimnúť, že f (x) sa nachádza nejednoznačne. Ako f (x) môžeme brať f (x) \u003d x 3 +1 f (x) \u003d x 3 +2 f (x) \u003d x 3 -3 atď.

Pretože derivát každého z nich sa rovná 3x 2. (Derivácia konštanty je 0). Všetky tieto funkcie sa navzájom konštantne líšia. Preto môžeme všeobecné riešenie úlohy napísať v tvare f (x) \u003d x 3 + C, kde C predstavuje akékoľvek konštantné reálne číslo.

Zavolá sa ktorákoľvek z nájdených funkcií f (x) primitívne pre funkciu F` (x) \u003d 3x 2

Definícia.

Funkcia F (x) sa nazýva primitívna pre funkciu f (x) v danom intervale J, ak pre všetky x z tohto intervalu F` (x) \u003d f (x). Funkcia F (x) \u003d x 3 je teda primitívom pre f (x) \u003d 3x 2 na (- ∞; ∞). Pretože pre všetky x ~ R platí rovnosť: F` (x) \u003d (x 3) `\u003d 3x 2

Ako sme už poznamenali, táto funkcia má nekonečné množstvo primitívnych látok.

Príklad č.

Funkcia je primitívom pre všetky na intervale (0; + ∞), od pre všetky h z tohto intervalu platí rovnosť.

Integračným problémom je nájsť všetky jeho výhody pre danú funkciu. Pri riešení tohto problému zohráva dôležitú úlohu nasledujúce tvrdenie:

Značka stálosti funkcie. Ak F "(x) \u003d 0 v nejakom intervale I, potom je funkcia F v tomto intervale konštantná.

Dôkazy.

Opravíme nejaké x 0 z intervalu I. Potom pre každé číslo x z takého intervalu môžeme na základe Lagrangeovho vzorca určiť číslo c medzi x a x 0 tak, aby

F (x) - F (x 0) \u003d F "(c) (x-x 0).

Podľa hypotézy F ‘(с) \u003d 0, pretože с ∈1 teda

F (x) - F (x 0) \u003d 0.

Takže pre všetkých x z intervalu I

to znamená, že funkcia F zostáva konštantná.

Všetky primitívne funkcie funkcie f je možné napísať pomocou jedného vzorca, ktorý sa volá všeobecná forma primitívnych látok pre funkciu f. Nasledujúca veta je pravdivá ( hlavná vlastnosť primitívnych liekov):

Veta. Akékoľvek primitívne funkcie pre funkciu f na intervale I je možné napísať ako

F (x) + C, (1) kde F (x) je jedným z primitívnych činiteľov pre funkciu f (x) na intervale I a C je ľubovoľná konštanta.

Vysvetlime si toto tvrdenie, v ktorom sú stručne formulované dve vlastnosti primitívneho činidla:

akékoľvek číslo, ktoré dáme do výrazu (1) namiesto С, dostaneme primitívum pre f na intervale I;
nezáleží na tom, aké primitívne funkcie Φ pre f vezmeme na interval I, môžeme zvoliť číslo C také, aby pre všetky x z intervalu I bola rovnosť

Dôkazy.

Podľa hypotézy je funkcia F primitívom pre f na intervale I. Preto F "(x) \u003d f (x) pre ľubovoľné x∈1, teda (F (x) + C)" \u003d F "(x) + C "\u003d f (x) + 0 \u003d f (x), to znamená, že F (x) + C je primitívne pre funkciu f.
Nech Ф (х) je jedným z primitívnych činiteľov pre funkciu f na rovnakom intervale I, to znamená Ф "(x) \u003d f (х) pre všetky x∈I.

Potom (Ф (x) - F (x)) "\u003d Ф" (x) -F '(x) \u003d f (x) -f (x) \u003d 0.

Preto to nasleduje dovnútra. sila znamienka konštantnosti funkcie, že rozdiel Ф (х) - F (х) je funkcia, ktorá na intervale I nadobúda konštantnú hodnotu С.

Teda pre všetky x z intervalu I platí podľa potreby rovnosť Φ (x) - F (x) \u003d C. Môže byť uvedená hlavná vlastnosť antiderivátu geometrický význam: grafy ľubovoľných dvoch primitívnych funkcií pre funkciu f sa získajú navzájom paralelným prekladom pozdĺž osi Oy

Otázky k poznámkam

Funkcia F (x) je primitívom pre funkciu f (x). Nájdite F (1), ak f (x) \u003d 9x2 - 6x + 1 a F (-1) \u003d 2.

Nájdite všetky výhody pre funkciu

Pre funkciu (x) \u003d cos2 * sin2x nájdite primitívne funkcie F (x), ak F (0) \u003d 0.

Pre túto funkciu vyhľadajte primitívne funkcie, ktorých graf prechádza bodom