$X$. Başlangıç olarak aşağıdaki tanımı hatırlayın:
Tanım 1
Nüfus- belirli değerleri elde etmek amacıyla üzerinde gözlemlerin yapıldığı, belirli bir türden rastgele seçilmiş nesneler kümesi rastgele değişken Belirli bir türden bir rastgele değişken incelenirken sabit koşullar altında gerçekleştirilir.
Tanım 2
Genel varyans-- ortalama karelerin aritmetiği bir popülasyon değişkeninin değerlerinin ortalama değerlerinden sapmaları.
$x_1,\ x_2,\dots ,x_k$ seçeneğinin değerleri sırasıyla $n_1,\ n_2,\dots ,n_k$ frekanslarına sahip olsun. Daha sonra genel varyans formülle hesaplanır:
Hadi düşünelim özel durum. Tüm seçenekler $x_1,\ x_2,\dots ,x_k$ farklı olsun. Bu durumda $n_1,\ n_2,\dots ,n_k=1$. Bu durumda genel varyansın aşağıdaki formül kullanılarak hesaplandığını görüyoruz:
Bu kavram aynı zamanda genel standart sapma kavramıyla da ilişkilidir.
Tanım 3
Genel ortalama standart sapma
\[(\sigma )_g=\sqrt(D_g)\]
Örnek varyans
Bize $X$ rastgele değişkenine göre örnek bir popülasyon verilsin. Başlangıç olarak aşağıdaki tanımı hatırlayın:
Tanım 4
Örnek popülasyon -- genel popülasyondan seçilen nesnelerin bir kısmı.
Tanım 5
Örnek varyans-- ortalama aritmetik değerlerörnekleme seçeneği
$x_1,\ x_2,\dots ,x_k$ seçeneğinin değerleri sırasıyla $n_1,\ n_2,\dots ,n_k$ frekanslarına sahip olsun. Daha sonra örnek varyansı aşağıdaki formül kullanılarak hesaplanır:
Özel bir durumu ele alalım. Tüm seçenekler $x_1,\ x_2,\dots ,x_k$ farklı olsun. Bu durumda $n_1,\ n_2,\dots ,n_k=1$. Bu durumda örneklem varyansının aşağıdaki formülle hesaplandığını görüyoruz:
Bu kavramla ilgili olarak örnek standart sapma kavramı da vardır.
Tanım 6
Numune standart sapması -- Kare kök genel varyanstan:
\[(\sigma )_в=\sqrt(D_в)\]
Düzeltilmiş varyans
Düzeltilmiş $S^2$ varyansını bulmak için örnek varyansı $\frac(n)(n-1)$ kesiriyle çarpmak gerekir, yani
Bu kavram aynı zamanda aşağıdaki formülle bulunan düzeltilmiş standart sapma kavramıyla da ilişkilidir:
Varyantların değerlerinin ayrı olmaması, ancak aralıkları temsil etmesi durumunda, genel veya örnek varyansların hesaplanmasına yönelik formüllerde, $x_i$ değeri, aralığın ortasının değeri olarak alınır. $x_i.$ ait.
Varyansı ve standart sapmayı bulmaya yönelik bir problem örneği
örnek 1
Örnek popülasyon aşağıdaki dağıtım tablosuyla tanımlanır:
Resim 1.
Bunun için örneklem varyansını, örneklem standart sapmasını, düzeltilmiş varyansını ve düzeltilmiş standart sapmasını bulalım.
Bu sorunu çözmek için önce bir hesaplama tablosu hazırlıyoruz:
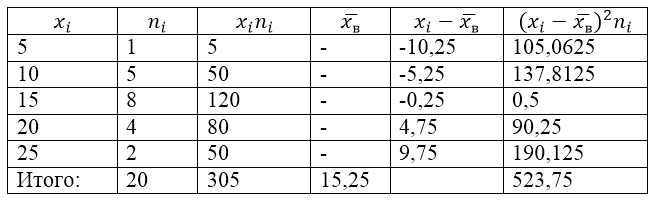
Şekil 2.
Tablodaki $\overline(x_в)$ (örnek ortalama) değeri şu formülle bulunur:
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15.25\]
Aşağıdaki formülü kullanarak örnek varyansını bulalım:
Numune standart sapması:
\[(\sigma )_в=\sqrt(D_в)\yaklaşık 5,12\]
Düzeltilmiş varyans:
\[(S^2=\frac(n)(n-1)D)_в=\frac(20)(19)\cdot 26.1875\approx 27.57\]
Düzeltilmiş standart sapma.
Excel programı hem profesyoneller hem de amatörler tarafından oldukça değerlidir, çünkü her beceri seviyesindeki kullanıcılar onunla çalışabilir. Örneğin, Excel'de minimum "iletişim" becerisine sahip olan herkes basit bir grafik çizebilir, düzgün bir tablo hazırlayabilir vb.
Aynı zamanda bu program, örneğin hesaplamalar gibi çeşitli hesaplama türlerini gerçekleştirmenize bile izin verir, ancak bu biraz farklı bir eğitim seviyesi gerektirir. Ancak bu programla yeni yeni tanışmaya başladıysanız ve daha ileri düzey bir kullanıcı olmanıza yardımcı olacak her şeyle ilgileniyorsanız bu makale tam size göre. Bugün size Excel'deki standart sapma formülünün ne olduğunu, neden buna ihtiyaç duyulduğunu ve kesin olarak ne zaman kullanıldığını anlatacağım. Gitmek!
Ne olduğunu
Teoriyle başlayalım. Standart sapmaya genellikle mevcut miktarlar arasındaki tüm kare farkların aritmetik ortalamasından ve bunların aritmetik ortalamasından elde edilen karekök denir. Bu arada, bu değere genellikle Yunanca "sigma" harfi denir. Standart sapma STANDART DEVAL formülü kullanılarak hesaplanır; buna göre program bunu kullanıcının kendisi için yapar.
Önemli olan bu kavram enstrümanın değişkenlik derecesini belirlemektir, yani bu, kendi tarzında, başlangıçta tanımlayıcı istatistiklerden gelen bir göstergedir. Belirli bir zaman diliminde bir enstrümanın volatilitesindeki değişiklikleri tanımlar. Standart sapma formüllerini kullanarak tahmin edebilirsiniz. standart sapma getirilirken mantıksal ve metin değerleri dikkate alınmaz.
Formül
Standart sapmanın hesaplanmasına yardımcı olur excel formülü otomatik olarak sağlanan Excel programı. Bunu bulmak için Excel'de formül bölümünü bulmanız ve ardından STANDART DEĞER adlı bölümü seçmeniz gerekir, bu nedenle çok basittir.
Bundan sonra önünüzde hesaplama için veri girmeniz gereken bir pencere görünecektir. Özellikle, özel alanlara iki sayı girilmelidir, bundan sonra programın kendisi numunenin standart sapmasını hesaplayacaktır.

Kuşkusuz matematiksel formüller ve hesaplamalar oldukça karmaşık bir konudur ve her kullanıcı bununla hemen başa çıkamaz. Ancak biraz daha derine inip konuya biraz daha detaylı bakarsanız her şeyin o kadar da üzücü olmadığı ortaya çıkıyor. Umarım standart sapmayı hesaplama örneğini kullanarak buna ikna olmuşsunuzdur.
Yardımcı olacak video
Bilge matematikçiler ve istatistikçiler, biraz farklı bir amaç için olsa da, daha güvenilir bir gösterge ortaya çıkardılar: ortalama doğrusal sapma . Bu gösterge, bir veri kümesinin değerlerinin ortalama değerleri etrafındaki dağılım ölçüsünü karakterize eder.
Veri dağılımının ölçüsünü göstermek için öncelikle bu dağılımın neyle hesaplanacağına karar vermelisiniz; genellikle bu ortalama değerdir. Daha sonra analiz edilen veri setinin değerlerinin ortalamadan ne kadar uzakta olduğunu hesaplamanız gerekir. Her değerin belirli bir sapma değerine karşılık geldiği açıktır ancak biz tüm popülasyonu kapsayan genel değerlendirmeyle ilgileniyoruz. Bu nedenle ortalama sapma, olağan aritmetik ortalama formülü kullanılarak hesaplanır. Ancak! Ancak sapmaların ortalamasını hesaplamak için önce bunların eklenmesi gerekir. Ve eğer pozitif ve negatif sayıları toplarsak, bunlar birbirini götürecek ve toplamları sıfıra yaklaşacaktır. Bunu önlemek için tüm sapmalar modülo olarak alınır, yani tüm negatif sayılar pozitif olur. Artık ortalama sapma, değerlerin yayılmasının genelleştirilmiş bir ölçüsünü gösterecektir. Sonuç olarak, ortalama doğrusal sapma aşağıdaki formül kullanılarak hesaplanacaktır:
A– ortalama doğrusal sapma,
X- analiz edilen gösterge, üstünde tire işaretiyle birlikte - göstergenin ortalama değeri,
N– analiz edilen veri setindeki değerlerin sayısı,
Umarım toplama operatörü kimseyi korkutmaz.
Belirtilen formül kullanılarak hesaplanan ortalama doğrusal sapma, belirli bir popülasyon için ortalama değerden ortalama mutlak sapmayı yansıtır.

Resimde kırmızı çizgi ortalama değerdir. Her gözlemin ortalamadan sapmaları küçük oklarla gösterilmiştir. Modülo olarak alınırlar ve toplanırlar. Daha sonra her şey değerlerin sayısına bölünür.
Resmi tamamlamak için bir örnek vermemiz gerekiyor. Diyelim ki kürek kesimleri üreten bir firma var. Her kesim 1,5 metre uzunluğunda olmalı ama daha da önemlisi hepsi aynı veya en az artı eksi 5 cm olmalıdır. dikkatsiz işçiler bazen 1,2 m, bazen 1,8 m kesiyorlar. Yazlılar mutsuz oluyor. Şirketin müdürü kesimlerin uzunluğunun istatistiksel bir analizini yapmaya karar verdi. 10 parça seçip uzunluklarını ölçtüm, ortalamasını buldum ve ortalama doğrusal sapmayı hesapladım. Ortalamanın tam olarak ihtiyaç duyulan şey olduğu ortaya çıktı - 1,5 m, ancak ortalama doğrusal sapma 0,16 m idi, yani her kesimin ortalama 16 cm daha uzun veya daha kısa olduğu ortaya çıktı. işçiler. Aslında bu göstergenin gerçek bir kullanımını görmedim, bu yüzden kendim bir örnek buldum. Ancak istatistiklerde böyle bir gösterge var.
Dağılım
Ortalama doğrusal sapma gibi varyans da verilerin ortalama değer etrafındaki yayılma boyutunu yansıtır.
Varyansı hesaplama formülü şuna benzer:
 (Varyasyon serileri için (ağırlıklandırılmış varyans))
(Varyasyon serileri için (ağırlıklandırılmış varyans))
 (gruplanmamış veriler için (basit varyans))
(gruplanmamış veriler için (basit varyans))
Burada: σ 2 – dağılım, Şi– kare göstergesini (karakteristiğin değeri) analiz ediyoruz, – göstergenin ortalama değeri, f i – analiz edilen veri setindeki değerlerin sayısı.
Dağılım sapmaların ortalama karesidir.
İlk önce ortalama değer hesaplanır, daha sonra her bir orijinal değer ile ortalama değer arasındaki fark alınır, karesi alınır, karşılık gelen nitelik değerinin frekansıyla çarpılır, eklenir ve ardından popülasyondaki değer sayısına bölünür.
Ancak, saf formu Aritmetik ortalama veya indeks gibi varyans kullanılmaz. Daha ziyade diğer istatistiksel analiz türleri için kullanılan yardımcı ve ara bir göstergedir.
Varyansı hesaplamanın basitleştirilmiş bir yolu
![]()
Standart sapma
Varyansı veri analizinde kullanmak için varyansın karekökü alınır. Sözde olduğu ortaya çıktı standart sapma.

Bu arada, standart sapmaya aynı zamanda onu ifade eden Yunanca harften sigma da denir.
Standart sapma elbette veri dağılımının ölçüsünü de karakterize eder, ancak artık (varyanstan farklı olarak) orijinal verilerle karşılaştırılabilir. Kural olarak istatistiklerdeki kök ortalama kare ölçümleri doğrusal ölçümlerden daha doğru sonuçlar verir. Bu nedenle standart sapma, verilerin dağılımının doğrusal ortalama sapmadan daha doğru bir ölçüsüdür.
Standart sapma(eş anlamlı: standart sapma, standart sapma, kare sapma; ilgili terimler: standart sapma, standart yayılma) - olasılık teorisi ve istatistikte, rastgele bir değişkenin değerlerinin matematiksel beklentisine göre dağılımının en yaygın göstergesi. Değer örneklerinin sınırlı dizileri ile matematiksel beklenti yerine örnek kümesinin aritmetik ortalaması kullanılır.
Ansiklopedik YouTube
-
1 / 5
Standart sapma, rastgele değişkenin kendisinin ölçüm birimlerinde ölçülür ve aritmetik ortalamanın standart hatasını hesaplarken, güven aralıkları oluştururken, hipotezleri istatistiksel olarak test ederken, rastgele değişkenler arasındaki doğrusal ilişkiyi ölçerken kullanılır. Bir rastgele değişkenin varyansının karekökü olarak tanımlanır.
Standart sapma:
s = n n - 1 σ 2 = 1 n - 1 ∑ ben = 1 n (x ben - x¯) 2 ; (\displaystyle s=(\sqrt ((\frac (n)(n-1))\sigma ^(2)))=(\sqrt ((\frac (1)(n-1))\sum _( i=1)^(n)\left(x_(i)-(\bar (x))\right)^(2)));)- Not: Çoğu zaman MSD (Kök Ortalama Kare Sapma) ve STD (Standart Sapma) adlarında formülleriyle arasında farklılıklar vardır. Örneğin Python programlama dilinin numPy modülünde std() fonksiyonu "standart sapma" olarak tanımlanırken formül standart sapmayı (örnekliğin köküne bölünmesi) yansıtır. Excel'de STANDARDDEVAL() işlevi farklıdır (n-1'in köküne göre bölme).
Standart sapma(rastgele bir değişkenin standart sapmasının tahmini X varyansının tarafsız bir tahminine dayanan matematiksel beklentisine göre) s (\displaystyle s):
σ = 1 n ∑ ben = 1 n (x ben - x ¯) 2 . (\displaystyle \sigma =(\sqrt ((\frac (1)(n))\sum _(i=1)^(n)\left(x_(i)-(\bar (x))\right) ^(2))))Nerede σ 2 (\displaystyle \sigma ^(2))- dağılım; x ben (\displaystyle x_(i)) - Ben seçimin inci unsuru; n (\displaystyle n)- örnek boyut;
- numunenin aritmetik ortalaması:x ¯ = 1 n ∑ ben = 1 n x ben = 1 n (x 1 + … + x n) . (\displaystyle (\bar (x))=(\frac (1)(n))\sum _(i=1)^(n)x_(i)=(\frac (1)(n))(x_ (1)+\ldots +x_(n))).)
Her iki tahminin de taraflı olduğunu belirtmek gerekir. Genel durumda tarafsız bir tahmin yapmak mümkün değildir. Ancak tarafsız varyans tahminine dayalı tahmin tutarlıdır.
GOST R 8.736-2011 uyarınca standart sapma bu bölümün ikinci formülü kullanılarak hesaplanır. Lütfen sonuçları kontrol edin.
GOST R 8.736-2011 uyarınca standart sapma bu bölümün ikinci formülü kullanılarak hesaplanır. Lütfen sonuçları kontrol edin. (Üç sigma kuralı 3 σ (\displaystyle 3\sigma ) ) - normal olarak dağıtılan bir rastgele değişkenin neredeyse tüm değerleri aralıkta yer alır(x ¯ − 3 σ ; x ¯ + 3 σ) (\displaystyle \left((\bar (x))-3\sigma ;(\bar (x))+3\sigma \right)) . Daha kesin olarak - yaklaşık 0,9973 olasılıkla, normal olarak dağıtılan bir rastgele değişkenin değeri belirtilen aralıkta yer alır (değerin x¯ (\displaystyle (\bar (x)))
doğrudur ve numune işleme sonucunda elde edilmemiştir). . Daha kesin olarak - yaklaşık 0,9973 olasılıkla, normal olarak dağıtılan bir rastgele değişkenin değeri belirtilen aralıkta yer alır (değerin Gerçek değer ise bilinmiyorsa kullanmamalısınızσ (\displaystyle \sigma) , A S . Böylece,üç kuralı , A .
sigma üç kuralına dönüştürülür
Standart sapma değerinin yorumlanması
Daha büyük bir standart sapma değeri, sunulan setteki değerlerin, setin ortalama değeri ile daha büyük bir yayılımını gösterir; buna göre daha küçük bir değer, kümedeki değerlerin ortalama değer etrafında gruplandığını gösterir. Mesela elimizde üç tane var sayısal kümeler : (0, 0, 14, 14), (0, 6, 8, 14) ve (6, 6, 8, 8). Her üç kümenin de ortalama değerleri 7'ye ve standart sapmaları sırasıyla 7, 5 ve 1'e eşittir. Son kümenin küçük bir standart sapması vardır, çünkü kümedeki değerler ortalama değer etrafında gruplandırılmıştır; ilk set en fazlasına sahip büyük önem
Genel anlamda standart sapma bir belirsizlik ölçüsü olarak düşünülebilir. Örneğin fizikte standart sapma, bir niceliğin ardışık ölçümlerinin hatasını belirlemek için kullanılır. Bu değer, teorinin öngördüğü değerle karşılaştırıldığında incelenen olgunun makullüğünü belirlemek için çok önemlidir: ölçümlerin ortalama değeri teorinin öngördüğü değerlerden büyük ölçüde farklıysa (büyük standart sapma), daha sonra elde edilen değerler veya bunları elde etme yöntemi yeniden kontrol edilmelidir. portföy riski ile tanımlanır.
İklim
Diyelim ki aynı ortalama maksimum günlük sıcaklığa sahip iki şehir var, ancak biri sahilde, diğeri ise ovada bulunuyor. Kıyıda yer alan şehirlerin birçok farklı maksimum gündüz sıcaklığına sahip olduğu ve iç kesimlerde bulunan şehirlerden daha düşük olduğu bilinmektedir. Bu nedenle, bu değerin ortalama değeri aynı olmasına rağmen, bir kıyı kenti için maksimum günlük sıcaklıkların standart sapması, ikinci şehre göre daha az olacaktır; bu, pratikte maksimum hava sıcaklığının aynı bölgede olma ihtimali anlamına gelir. yılın herhangi bir gününde ortalama değerden farklı olarak iç kesimlerde bulunan bir şehir için daha yüksek olacaktır.
Spor
Atılan ve yenen gol sayısı, gol şansı vb. gibi bazı parametrelere göre derecelendirilen birkaç futbol takımının olduğunu varsayalım. Bu gruptaki en iyi takımın daha iyi değerlere sahip olması muhtemeldir. daha fazla parametre üzerinde. Sunulan parametrelerin her biri için takımın standart sapması ne kadar küçük olursa, bu tür takımların sonucu o kadar öngörülebilir olur; Öte yandan takımla büyük bir değer Standart sapmanın sonucu tahmin etmek zordur ve bu da dengesizlikle açıklanır, örneğin: güçlü savunma, ancak zayıf bir saldırıyla.
Takım parametrelerinin standart sapmasını kullanmak, iki takım arasındaki bir maçın sonucunu bir dereceye kadar tahmin etmeyi, güçlü yönleri değerlendirmeyi ve zayıf taraflar emirler ve dolayısıyla seçilen mücadele yöntemleri.
Bu varyans hesaplamasının bir dezavantajı olduğunu belirtmekte fayda var - önyargılı olduğu ortaya çıkıyor, yani. o beklenen değer varyansın gerçek değerine eşit değildir. Bu konuda daha fazlasını okuyun. Aynı zamanda her şey o kadar da kötü değil. Örneklem büyüklüğü arttıkça hala teorik analoguna yaklaşmaktadır. asimptotik olarak tarafsızdır. Bu nedenle, birlikte çalışırken büyük boyutlarörnekler için yukarıdaki formülü kullanabilirsiniz.
İşaret dilini sözcük diline çevirmek faydalıdır. Varyansın sapmaların ortalama karesi olduğu ortaya çıktı. Yani önce ortalama değer hesaplanır, ardından her orijinal değer ile ortalama değer arasındaki fark alınır, karesi alınır, eklenir ve ardından popülasyondaki değer sayısına bölünür. Bireysel değer ile ortalama arasındaki fark, sapmanın ölçüsünü yansıtır. Tüm sapmaların yalnızca pozitif sayılar haline gelmesi ve toplanırken pozitif ve negatif sapmaların karşılıklı olarak yok edilmesini önlemek için kareleri alınır. Daha sonra, sapmaların kareleri verildiğinde, basitçe aritmetik ortalamayı hesaplarız. Ortalama - kare - sapmalar. Sapmaların karesi alınır ve ortalaması hesaplanır. Çözüm sadece üç kelimede yatıyor.
Ancak aritmetik ortalama veya indeks gibi saf haliyle dağılım kullanılmaz. Daha ziyade diğer istatistiksel analiz türleri için gerekli olan yardımcı ve ara bir göstergedir. Normal bir ölçü birimi bile yok. Formüle bakılırsa, bu orijinal verilerin ölçü biriminin karesidir. Dedikleri gibi, şişe olmadan çözemezsiniz.
(modül 111)
Varyansı gerçeğe döndürmek, yani onu daha sıradan amaçlar için kullanmak için, bundan karekök çıkarılır. Sözde olduğu ortaya çıktı standart sapma (RMS). “Standart sapma” veya “sigma” (Yunanca harfin adından) isimleri vardır. Standart sapma formülü şöyledir:

Numune için bu göstergeyi elde etmek için aşağıdaki formülü kullanın:

Varyansta olduğu gibi, biraz farklı bir hesaplama seçeneği vardır. Ancak örneklem büyüdükçe fark ortadan kalkıyor.
Standart sapma, elbette, veri dağılımının ölçüsünü de karakterize eder, ancak artık (dağılımın aksine) aynı ölçüm birimlerine sahip oldukları için orijinal verilerle karşılaştırılabilir (bu, hesaplama formülünden açıktır). Ancak saf haliyle bu gösterge, kafa karıştırıcı çok fazla ara hesaplama (sapma, kare, toplam, ortalama, kök) içerdiğinden pek bilgilendirici değildir. Ancak standart sapmayla doğrudan çalışmak zaten mümkün çünkü bu göstergenin özellikleri iyi çalışılmış ve biliniyor. Mesela şu var üç sigma kuralı, verilerin aritmetik ortalamanın ±3 sigma dahilinde 1000 üzerinden 997 değerine sahip olduğunu belirtir. Belirsizliğin bir ölçüsü olarak standart sapma birçok istatistiksel hesaplamada da yer almaktadır. Yardımı ile çeşitli tahmin ve tahminlerin doğruluk derecesi belirlenir. Eğer varyasyon çok büyükse, standart sapma da büyük olacaktır ve dolayısıyla tahmin hatalı olacaktır; bu da örneğin çok geniş güven aralıklarında ifade edilecektir.
Değişim katsayısı
Standart sapma, dağılım ölçüsünün mutlak bir tahminini verir. Bu nedenle, yayılımın değerlerin kendisine göre ne kadar büyük olduğunu anlamak için (yani ölçeklerine bakılmaksızın) göreceli bir gösterge gereklidir. Bu gösterge denir varyasyon katsayısı ve aşağıdaki formül kullanılarak hesaplanır:
Değişim katsayısı yüzde olarak ölçülür (%100 ile çarpılırsa). Bu göstergeyi kullanarak, ölçekleri ve ölçü birimleri ne olursa olsun çeşitli olayları karşılaştırabilirsiniz. Bu gerçek ve varyasyon katsayısını bu kadar popüler hale getiriyor.
İstatistiklerde, varyasyon katsayısının değeri %33'ün altında ise popülasyonun homojen olduğu, %33'ün üzerinde ise heterojen olduğu kabul edilmektedir. Burada herhangi bir şey hakkında yorum yapmak benim için zor. Bunu kimin ve neden tanımladığını bilmiyorum ama bu bir aksiyom olarak kabul ediliyor.
Kuru teoriye kapıldığımı ve görsel ve mecazi bir şeyler getirmem gerektiğini hissediyorum. Öte yandan, tüm varyasyon göstergeleri yaklaşık olarak aynı şeyi açıklar, ancak farklı hesaplanırlar. Bu nedenle çeşitli örnekler göstermek zordur, ancak göstergelerin yalnızca değerleri farklılık gösterebilir, ancak özleri farklılık gösteremez. Öyleyse aynı veri seti için farklı varyasyon göstergelerinin değerlerinin nasıl farklılaştığını karşılaştıralım. Ortalama doğrusal sapmanın ('dan) hesaplanması örneğini ele alalım. İşte kaynak veriler:

Ve sana hatırlatacak bir program.

Bu verileri kullanarak hesaplıyoruz çeşitli göstergeler varyasyonlar.
Ortalama değer olağan aritmetik ortalamadır.
Değişim aralığı maksimum ve minimum arasındaki farktır:
Ortalama doğrusal sapma aşağıdaki formül kullanılarak hesaplanır:
Standart sapma:
Hesaplamayı bir tabloda özetleyelim.

Görüldüğü gibi doğrusal ortalama ve standart sapma, veri değişiminin derecesi için benzer değerler vermektedir. Varyans sigma kare olduğundan her zaman göreceli olacaktır Büyük bir sayı Aslında bu hiçbir şey ifade etmiyor. Değişim aralığı, aşırı değerler arasındaki farktır ve çok şey konuşabilir.
Bazı sonuçları özetleyelim.
Bir göstergenin değişmesi, bir sürecin veya olgunun değişkenliğini yansıtır. Derecesi çeşitli göstergeler kullanılarak ölçülebilir.
1. Değişim aralığı - maksimum ve minimum arasındaki fark. Aralığı yansıtır olası değerler.
2. Ortalama doğrusal sapma – analiz edilen popülasyonun tüm değerlerinin ortalama değerlerinden mutlak (modülo) sapmalarının ortalamasını yansıtır.
3. Dağılım - sapmaların ortalama karesi.
4. Standart sapma, dağılımın köküdür (sapmaların ortalama karesi).
5. Değişim katsayısı, ölçek ve ölçü birimlerine bakılmaksızın değerlerin dağılma derecesini yansıtan en evrensel göstergedir. Değişim katsayısı yüzde olarak ölçülür ve farklı süreç ve olayların değişimini karşılaştırmak için kullanılabilir.Böylece, istatistiksel analiz fenomenlerin homojenliğini ve süreçlerin istikrarını yansıtan bir göstergeler sistemi vardır. Genellikle varyasyon göstergelerinin bağımsız bir anlamı yoktur ve daha fazla veri analizi için kullanılır (güven aralıklarının hesaplanması)


