Nauczyciel najwyższa kategoria: Minaichenko N.S., gimnazjum nr 24, Sewastopol
Lekcja w 8 klasie: „Trójmian kwadratowy i jego korzenie”
Rodzaj lekcji : lekcja nowej wiedzy.
Cel lekcji:
organizować zajęcia uczniów w celu utrwalenia i rozwijania wiedzy na temat rozkładu trójmian kwadratowy na współczynnikach liniowych redukcja ułamków;
rozwijać umiejętności stosowania wiedzy z zakresu wszystkich metod faktoryzacji: nawiasów, stosowania wzorów mnożenia skróconego i metody grupowania w celu przygotowania się do udana dostawa egzamin z algebry;
stworzyć warunki do rozwoju zainteresowania poznawczego przedmiotem, formacji logiczne myślenie i samokontroli podczas korzystania z faktoryzacji.
Ekwipunek: rzutnik multimedialny, ekran, prezentacja: „Korzenie trójmianu kwadratowego”, krzyżówka, test, handout.
Podstawowe koncepcje . Faktoryzacja trójmianu kwadratowego.
Samodzielna aktywność studentów. Zastosowanie twierdzenia o faktoryzacji dla trójmianu kwadratowego w rozwiązywaniu problemów.
Plan lekcji
Rozwiązywanie problemów.Odpowiedzi na pytania uczniów
IV. Podstawowy sprawdzian opanowania wiedzy. Odbicie
Wiadomość od nauczyciela.
Wiadomość dla ucznia
v. Praca domowa
pisanie na tablicy
Komentarz metodologiczny:
Ten temat jest fundamentalny w sekcji „ Transformacje tożsamości wyrażenia algebraiczne”. Dlatego ważne jest, aby uczniowie automatycznie mogli nie tylko zobaczyć wzory na faktoryzację w przykładach, ale także zastosować je w innych zadaniach: takich jak rozwiązywanie równań, przekształcanie wyrażeń, udowadnianie tożsamości.
Ten temat koncentruje się na rozkładaniu trójmianu kwadratowego na czynniki:
topór+ bx + c = a(x – x)(x – x
),
gdzie x i x są pierwiastkami równania kwadratowego ax + bx + c = 0.
Pozwala to poszerzyć pole widzenia ucznia, nauczyć go myślenia w nietypowa sytuacja podczas korzystania z badanego materiału, tj. korzystając ze wzoru na faktoryzację trójmianu kwadratowego:
umiejętność redukcji ułamków algebraicznych;
umiejętność upraszczania wyrażeń algebraicznych;
umiejętność rozwiązywania równań;
umiejętność udowodnienia tożsamości.
Główna treść lekcji:
a) 3x + 5x - 2;
b) –x + 16x – 15;
c) x - 12x + 24;
d) -5x + 6x - 1.
№2. Zmniejsz ułamek:
№3. Uprość wyrażenie:
№4. Rozwiąż równanie:
b) 
Podczas zajęć:
I. Etap aktualizacji wiedzy.
Motywacja działalności edukacyjnej.
a) z historii:
b) krzyżówka:
Rozgrzewka-trening umysłu - krzyżówka:
Poziomo:
1) Korzeń drugiego stopnia nazywa się .... (kwadrat)
2) Zmienne wartości, przy których równanie staje się prawdziwą równością (korzenie)
3) Równość zawierająca nieznaną nazywa się ... (równanie)
4) indyjski naukowieckto przedstawił? główna zasada rozwiązywanie równań kwadratowych (Brahmagupta)
5) Współczynniki równania kwadratowego to ... (liczby)
6) Starożytny grecki naukowiec, który wynalazł geometryczną metodę rozwiązywania równań (Euklid)
7) Twierdzenie łączące współczynniki i pierwiastki równania kwadratowego (Vieta)
8) „rozróżnianie”, definiowanie pierwiastków równania kwadratowego to ... (dyskryminacja)
Do tego:
Jeśli D>0, ile pierwiastków? (dwa)
Jeśli D=0, ile pierwiastków? (jeden)
Jeśli D<0, сколько корней? (нет действительных корней)
Poziomo i pionowo temat lekcji: „Trójmian kwadratowy”
b) motywacja:
Temat ten jest fundamentalny w rozdziale „Przekształcenia tożsamościowe wyrażeń algebraicznych”. Dlatego ważne jest, aby automatycznie móc nie tylko zobaczyć wzory na faktoryzację w przykładach, ale także zastosować je w innych zadaniach: takich jak zmniejszanie ułamków, rozwiązywanie równań, przekształcanie wyrażeń, udowadnianie tożsamości.
Dzisiaj skupimy się na faktoryzacji trójmianu kwadratowego:
II. Nauka nowego materiału.
Temat: Trójmian kwadratowy i jego pierwiastki.
Ogólna teoria wielomianów w wielu zmiennych wykracza daleko poza zakres kursu szkolnego. Dlatego ograniczamy się do badania wielomianów jednej zmiennej rzeczywistej, i to nawet w najprostszych przypadkach. Rozważ wielomiany jednej zmiennej zredukowane do postaci standardowej.
Korzeń wielomianu jest wartością zmiennej, przy której wartość wielomianu jest równa zero. Oznacza to, że aby znaleźć pierwiastki wielomianu, konieczne jest zrównanie go z zero, tj. Rozwiązać równanie.
Pierwiastek wielomianu pierwszego stopnia 
łatwe do znalezienia 
. Badanie: 
.
Pierwiastki trójmianu kwadratowego można znaleźć, rozwiązując równanie: 
.
Zgodnie ze wzorem pierwiastków równania kwadratowego znajdujemy:
; 
Jeśli 
oraz 
- pierwiastki trójmianu kwadratowego 
, gdzie 
≠ 0,
następnie .
Dowód:
Wykonujemy następujące przekształcenia trójmianu kwadratowego:
=
=
=
=
=
=
=
=
Ponieważ dyskryminator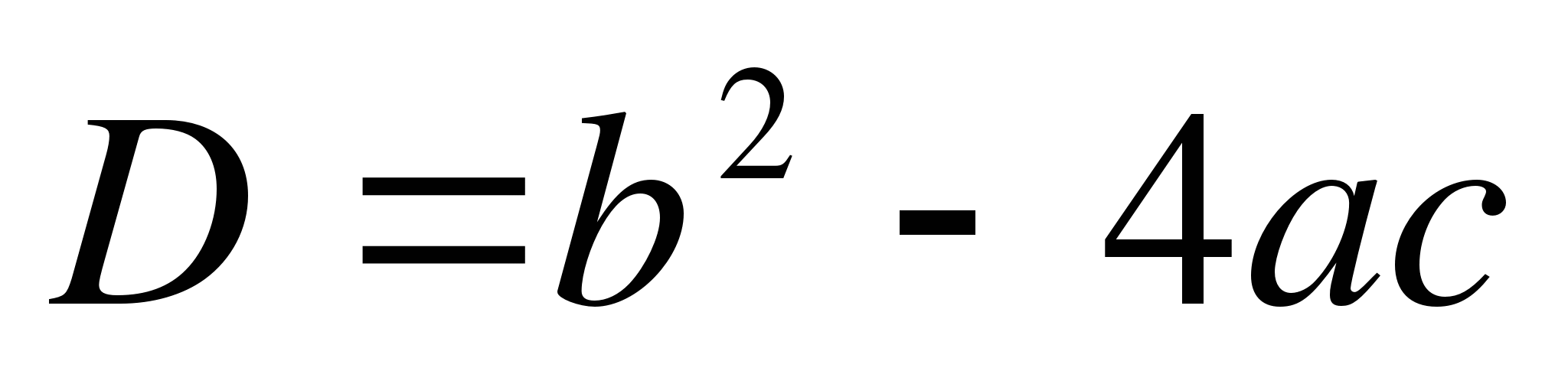 
otrzymujemy:
=
=
Stosujemy wzór różnicy kwadratów w nawiasach i otrzymujemy:
=
=
,
dlatego ; . Twierdzenie zostało udowodnione.
Powstała formuła nazywa się formułąfaktoryzacja trójmianu kwadratowego.
III. Kształtowanie umiejętności i zdolności.
№1. Rozkład na czynniki kwadratowe trójmianu:
a) 3x + 5x - 2;Rozwiązanie:
Odpowiedź: 3x+5x–2=3(x+2)(x-)=(x+2)(3x-1)
Na biurku:
b) –5x + 6x – 1;
Do tego:
c) x - 12x + 24;
d) –x + 16x – 15.
№2. Zmniejsz ułamek:
a)
№4. Rozwiąż równanie:
b)
IV. Podstawowy sprawdzian opanowania wiedzy.
a) Test.
Opcja 1.
1. Znajdź pierwiastki trójmianu kwadratowego:2x 2 -9x-5
Odpowiadać:
2. Który wielomian należy zastąpić wielomianem, aby równość była prawdziwa:
b) Wzajemna weryfikacja według opcji (odpowiedzi i parametry oceny są zilustrowane).
c) Refleksja.
V. Praca domowa.
Możesz znaleźć pierwiastek trójmianu kwadratowego poprzez dyskryminator. Ponadto dla wielomianu zredukowanego drugiego stopnia ważne jest twierdzenie Vieta, oparte na stosunku współczynników.
Instrukcja
- Równania kwadratowe to dość szeroki temat w szkolnej algebrze. Lewa strona takiego równania jest wielomianem drugiego stopnia postaci A x² + B x + C, tj. wyrażenie trzech jednomianów o różnym stopniu nieznanego x. Aby znaleźć pierwiastek z trójmianu kwadratowego, musisz obliczyć wartość x, dla której to wyrażenie jest równe zero.
- Aby rozwiązać równanie kwadratowe, musisz znaleźć dyskryminator. Jego wzór jest konsekwencją podświetlenia pełnego kwadratu wielomianu i jest pewnym stosunkiem jego współczynników: D = B² - 4 A C.
- Wyróżnik może przybierać różne wartości, w tym być negatywnym. A jeśli młodsi uczniowie mogą z ulgą powiedzieć, że takie równanie nie ma pierwiastków, to już licealiści potrafią je wyznaczyć na podstawie teorii liczb zespolonych. Tak więc mogą istnieć trzy opcje: Wyróżnik jest liczbą dodatnią. Wtedy pierwiastki równania to: x1 = (-B + √D)/2 A; x2 = (-B - √D) / 2 A;
Dyskryminator zszedł do zera. Teoretycznie w tym przypadku równanie ma również dwa pierwiastki, ale praktycznie są one takie same: x1 \u003d x2 \u003d -B / 2 A;
Dyskryminator jest mniejszy od zera. Do obliczeń wprowadzana jest pewna wartość i² = -1, która pozwala na zapisanie rozwiązania złożonego: x1 = (-B + i √|D|)/2 A; x2 \u003d (-B - i √ | D |) / 2 A. - Metoda dyskryminacyjna jest ważna dla dowolnego równania kwadratowego, jednak zdarzają się sytuacje, w których wskazane jest zastosowanie szybszej metody, zwłaszcza dla małych współczynników całkowitych. Metoda ta nazywana jest twierdzeniem Vieta i polega na parze relacji między współczynnikami w zredukowanym trójmianie: x² + P x + Q
x1 + x2 = -P;
x1 x2 = Q. Pozostaje tylko zebrać korzenie. - Należy zauważyć, że równanie można sprowadzić do podobnej postaci. Aby to zrobić, musisz podzielić wszystkie wyrazy trójmianu przez współczynnik w najwyższym stopniu A: A x² + B x + C | A
x² + B/A x + C/A
x1 + x2 = -B/A;
x1 x2 = C/A.
Opis lekcji wideo
Każde z wyrażeń to trzy x piąta potęga minus x czwarta potęga plus trzy x sześcian minus sześć x plus dwa; pięć Y potęgi czwartej minus sześcian Y plus pięć kwadratów Y minus trzy Y plus osiemnaście; trzy z potęgi szóstej minus a z potęgi czwartej plus kwadrat z minus a z plus dwa jest wielomianem jednej zmiennej.
Wartość zmiennej, przy której znika wielomian, nazywana jest pierwiastkiem wielomianu.
Znajdź na przykład pierwiastki wielomianu x odjąć cztery x. Aby to zrobić, rozwiązujemy równanie x sześcian minus cztery x równa się zero. Po rozłożeniu lewej strony równania na czynniki otrzymujemy iloczyn trzech czynników: x, x minus dwa i x plus dwa, równy zero. Stąd x pierwsze jest równe zeru, x drugie jest równe dwóm, x trzecie jest równe minus dwa.
Zatem liczby zero, dwa i minus dwa są pierwiastkami wielomianu x sześcianu minus cztery x ...
Wielomian drugiego stopnia z jedną zmienną nazywamy trójmianem kwadratowym.
Trójmian kwadratowy jest wielomianem postaci a x kwadrat plus be x plus ce, gdzie x jest zmienną, .. a, być i ce są pewne liczby, a a nie jest równe zeru.
Współczynnik a nazywany jest współczynnikiem starszym, ce jest swobodnym elementem trójmianu kwadratowego.
Przykładami trójmianów kwadratowych są wielomiany dwa x kwadrat minus x minus pięć; x kwadrat plus siedem x minus osiem. W pierwszym z nich a równa się dwa, be równe minus jeden, ce równe minus pięć, w drugim a równa się jeden, be równe siedem, ce równe minus osiem. Do trójmianów kwadratowych zalicza się również takie wielomiany drugiego stopnia, w których jeden ze współczynników be lub ce lub nawet oba są równe zero. Tak więc wielomian pięć x kwadrat minus dwa x jest uważany za trójmian kwadratowy. Współczynnik a jest równy pięć, be jest równe minus dwa, ce jest równe zeru.
Aby znaleźć pierwiastki trójmianu kwadratowego a x kwadrat plus be x plus ce, musisz rozwiązać równanie kwadratowe a x kwadrat plus be x plus ce wynosi zero.
Przykład pierwszy. Znajdź pierwiastki trójmianu kwadratowego x kwadrat odjąć trzy x odjąć cztery.
Aby to zrobić, przyrównujemy to wyrażenie do zera i rozwiązujemy wynikowe równanie kwadratowe. Wyróżnik to dwadzieścia pięć, pierwszy pierwiastek to cztery, drugi pierwiastek to minus jeden.
Zatem trójmian kwadratowy x kwadrat odjąć trzy x odjąć cztery ma dwa pierwiastki: cztery i minus jeden.
Ponieważ trójmian kwadratowy a x kwadrat plus ba x plus ce ma te same pierwiastki co równanie a x kwadrat plus ba x plus ce jest równe zero, to może, podobnie jak równanie kwadratowe, mieć dwa pierwiastki, jeden pierwiastek lub w ogóle nie mieć pierwiastków . Zależy ona od wartości dyskryminatora równania kwadratowego, który jest również nazywany dyskryminatorem trójmianu kwadratowego.Jeśli dyskryminator jest większy od zera, to trójmian kwadratowy ma dwa pierwiastki; jeśli dyskryminator wynosi zero, to trójmian kwadratowy ma jeden pierwiastek; jeśli dyskryminator jest mniejszy od zera, to trójmian kwadratowy nie ma pierwiastków.
Podczas rozwiązywania problemów czasami wygodnie jest przedstawić trójmian kwadratowy a x kwadrat plus be x plus ce jako sumę a pomnożoną przez kwadrat różnicy a i em ... oraz liczbę en, gdzie em i en są pewnymi liczbami . Takie przekształcenie nazywa się wyodrębnianiem kwadratu dwumianu z trójmianu kwadratu. Posłużmy się przykładem, aby pokazać, jak taka transformacja jest wykonywana.
Drugi przykład. Wybierz z trójmianu dwa x kwadrat minus cztery x plus sześć ... kwadrat dwumianu.
Wyciągamy czynnik dwa, .. następnie przekształcamy wyrażenie w nawiasy, dla których dodajemy i odejmujemy jeden ... W rezultacie otrzymujemy sumę podwojonego kwadratu różnicy między liczbami x i jeden .. I cyfry cztery.
Zatem dwa x do kwadratu minus cztery x plus sześć jest równe sumie dwukrotności kwadratu różnicy między liczbami x i jeden .. A liczby cztery ...
Rozważmy problem, którego rozwiązanie wykorzystuje wybór kwadratu dwumianu z trójmianu kwadratu.
Zadanie. Udowadniamy, że ze wszystkich prostokątów o obwodzie 20 cm kwadrat ma największą powierzchnię.
Niech jedna strona prostokąta będzie wynosić x centymetrów. Wtedy długość drugiego wyniesie dziesięć minus x centymetrów, a powierzchnia prostokąta jest równa iloczynowi tych boków.
Po otwarciu nawiasów w wyrażeniu x pomnożonym przez różnicę dziesięciu i x otrzymujemy dziesięć x minus x do kwadratu. Wyrażenie minus x kwadrat plus dziesięć x jest trójmianem kwadratowym, w którym współczynnik A wynosi minus jeden, be równy dziesięć, ce równa się zero. Wybierzmy kwadrat dwumianu i otrzymajmy wyrażenie minus kwadrat różnicy xi pięć .. plus dwadzieścia pięć.
Ponieważ wyrażenie minus kwadrat różnicy x i pięć dla dowolnego x nie równego pięciu jest ujemne, to całe wyrażenie minus kwadrat różnicy x i pięciu ... plus dwadzieścia pięć przyjmuje największą wartość dla x równy pięciu.
Oznacza to, że obszar będzie największy, gdy jeden z boków prostokąta będzie miał 5 cm. W tym przypadku drugi bok również ma 5 cm. Oznacza to, że ten prostokąt jest kwadratem.
Praktyka egzaminów z matematyki pokazuje, że zadania z parametrami są najtrudniejsze zarówno logicznie, jak i technicznie, a zatem umiejętność ich rozwiązania w dużej mierze decyduje o pomyślnym zdaniu egzaminu na dowolnym poziomie.
W problemach z parametrami, obok wielkości nieznanych, występują wielkości, których wartości liczbowe, choć nie są konkretnie wskazane, są uważane za znane i podane na pewnym zbiorze liczbowym. Jednocześnie parametry zawarte w warunku znacząco wpływają na logiczny i techniczny przebieg rozwiązania oraz formę odpowiedzi. Takie problemy można znaleźć w książce „514 problemów z parametrami” W literaturze z zakresu matematyki elementarnej istnieje wiele podręczników, podręczników problemowych, podręczników metodycznych, w których podane są problemy z parametrami. Ale większość z nich obejmuje wąski zakres zagadnień, skupiając się na przepisie, a nie na logice rozwiązywania problemów. Ponadto te, które odniosły największy sukces, już dawno stały się bibliograficzną rzadkością. Pod koniec pracy podana jest lista książek, z których artykuły pomogły sklasyfikować wypowiedzi na temat pracy. Najważniejszym jest Shakhmeister A.Kh Równania i nierówności z parametrami.
Głównym celem tej pracy jest wypełnienie niektórych znaczących luk w głównym kursie algebry oraz ustalenie faktów korzystania z własności funkcja kwadratowa, które pozwalają znacznie uprościć rozwiązywanie problemów związanych z lokalizacją pierwiastków równania kwadratowego względem niektórych punktów charakterystycznych.
Zadania robocze:
Ustal możliwe przypadki położenia pierwiastków trójmianu kwadratowego na linii rzeczywistej;
Zidentyfikuj algorytmy, które umożliwiają rozwiązywanie równań kwadratowych z parametrem opartym na położeniu pierwiastków trójmianu kwadratowego na linii rzeczywistej;
Naucz się rozwiązywać problemy o wyższej złożoności w porównaniu z poziomem obowiązkowym; opanować szereg technicznych i intelektualnych umiejętności matematycznych na poziomie ich swobodnego wykorzystania; doskonalenie kultury matematycznej w ramach szkolnego kursu matematyki.
Przedmiot badań: położenie korzeni trójmianu kwadratowego na linii współrzędnych.
Przedmiot badań: równania kwadratowe z parametrem.
Metody badawcze. Główne metody badania problemów z parametrem: analityczne, graficzne i kombinowane (funkcjonalno – graficzne). Analityczne to metoda tzw. rozwiązania bezpośredniego, powtarzająca standardowe procedury znajdowania odpowiedzi w problemach bez parametru. Graficzna to metoda, w której wykresy są używane w płaszczyźnie współrzędnych (x; y). Przejrzystość metody graficznej pomaga znaleźć szybki sposób rozwiązania problemu. Z tych dwóch metod ta ostatnia jest nie tylko elegancka, ale i najważniejsza, gdyż pokazuje związek między wszystkimi typami modelu matematycznego: słowny opis problemu, model geometryczny to wykres trójmianu kwadratowego, model analityczny to opis modelu geometrycznego układem nierówności skompilowany na podstawie zdań matematycznych ujawnionych przez wykres funkcji kwadratowej.
W wielu przypadkach rozwiązywanie równań kwadratowych z parametrem prowadzi do kłopotliwych przekształceń. Hipoteza: wykorzystanie właściwości funkcji kwadratowej znacznie uprości rozwiązanie, sprowadzając je do rozwiązania racjonalnych nierówności.
Główną częścią. Położenie pierwiastków trójmianu kwadratowego na linii współrzędnych
Rozważmy kilka stwierdzeń związanych z położeniem pierwiastków trójmianu kwadratowego f(x)=ax2+bx+с na prostej względem punktów m i n takich, że m
x1 i x2 to pierwiastki trójmianu kwadratowego,
D=b2-4ac- dyskryminator trójmianu kwadratowego, D≥0.
m, n, m1, m2, n1, n2 - podane liczby.
Wszystkie argumenty są brane pod uwagę dla a>0, przypadek dla a
Oświadczenie pierwsze
Aby liczba m znajdowała się między pierwiastkami trójmianu kwadratowego (x1
Dowód.
pod warunkiem x1
Interpretacja geometryczna
Niech x1 i x2 będą pierwiastkami równania. Dla a > 0 f(x)
Zadanie 1. Dla jakich wartości k równanie x2-(2k+1)x + 3k-4=0 ma dwa pierwiastki, z których jeden jest mniejszy od 2, a drugi większy od 2?
Rozwiązanie. f(x)=x2-(2k+1)x + 3k-4; x1
Dla k>-2 równanie x2-(2k+1)x + 3k-4=0 ma dwa pierwiastki, z których jeden jest mniejszy niż 2, a drugi większy niż 2.
Odpowiedź: k>-2.
Zadanie 2. Dla jakich wartości k równanie kx2+(3k-2)x + k-3=0 ma pierwiastki różnych znaków?
Problem ten można sformułować w następujący sposób: dla jakich wartości k liczba 0 leży między pierwiastkami tego równania.
Rozwiązanie (1 droga) f(x)= kx2+(3k-2)x + k-3; x1
Metoda 2 rozwiązań (przy użyciu twierdzenia Vieta). Jeśli równanie kwadratowe ma pierwiastki (D>0) i c/a
Zadanie 3. Dla jakich wartości k równanie (k2-2)x2+(k2+k-1)x – k3+k2=0 ma dwa pierwiastki, z których jeden jest mniejszy od k, a drugi większy od k?
f(x)=(k2-2)x2+(k2+k-1)x – k3+k2; x1 Podstawiając wartości k ze znalezionego zbioru, upewnimy się, że dla tych wartości k D>0.
Zdanie drugie (a)
Aby pierwiastki trójmianu kwadratowego były mniej niż liczba m(x1
Dowód: x1-m>0, x2-m 0; m2-mx1-mx2+x1x2>0; m2-(x1+x2)m+x1x2
Zadanie 4. Dla jakich wartości parametru pierwiastki równania x2-(3k+1)x+2k2+4k-6=0 mniejsze od -1?
D≥0; (3k+1)2-4(2k2+4k-6) ≥0; (k-5)2≥0; k - dowolny; x0-3/2; k0. 1+(3k+1)+(2k2+4k-6)>0. 2(k+4)(k-1/2)>0. k1/2
Oświadczenie drugie (b)
Aby pierwiastki trójmianu kwadratowego były więcej numeru m(m
D≥0; x0>m; af(m)>0.
Jeśli warunek m m. Ponieważ m nie należy do przedziału (x1; x2), to f(m) > 0 dla a > 0 i f(m)
I odwrotnie, niech utrzyma się system nierówności. Warunek D > 0 implikuje istnienie pierwiastków x1 i x2 (x1m.
Pozostaje wykazać, że x1 > m. Jeśli D = 0, to x1 = x2 > m. Jeśli D > 0, to f(x0) = -D/4a i af(x0) O, zatem w punktach x0 i m funkcja przyjmuje przeciwne znaki i x1 należy do przedziału (m;x0).
Zadanie 5. Dla jakich wartości parametru m pierwiastki równania x2-(3m+1)x+2m2+4m-6=0 a) są większe od 1? b) mniej niż -1?
Rozwiązanie a) D≥0; D≥0; (3m+1)2-4(2m2+4m-6) ≥0; x0>m; x0>1; ½(3m+1)>1; f(m)>0. f(1)>0. 1-(3m+1)+(2m2+4m-6)>0.
(m-5)2≥0; m - dowolne m>1/3; m>1/3;
(2km-3)(m+2)>0. m3/2. Odpowiedź: m>3/2.
b) D≥0; (3m+1)2-4(2m2+4m-6)≥0; (m-5)2 ≥0; m - dowolny x0-3/2; m0. 1+(3m+1)+(2m2+4m-6)>0. 2(m+4)(m-1/2)>0. m1/2.
Zadanie 6. Dla jakich wartości parametru są pierwiastki równania kx2-(2k +1)x+3 k -1=0 większe od 1?
Rozwiązanie. Oczywiście problem jest równoważny: dla jakich wartości parametru m są pierwiastki trójmianu kwadratowego większe niż 1?
D≥0; D≥0 (2k+1)2-4k (3k-1) ≥0; 8k2-8k-1≤0; x0>m; x0>1 (2k+1)/(2k)>1; 2k+1 > 2k; af(m)>0. af(1)>0. k(k-(2k+1)+(3k-1)) >0. 2k2-2k>0.
Rozwiązując ten system, stwierdzamy, że
Trzecie stwierdzenie
Aby pierwiastki trójmianu kwadratowego były większe niż liczba m i mniejsze niż n (m
D≥0; m 0 af(n)>0.
Notatka cechy charakteru grafika.
1) Równanie ma pierwiastki, co oznacza D > 0.
2) Oś symetrii znajduje się między liniami x \u003d m i x \u003d n, co oznacza m
3) W punktach x \u003d m i x \u003d n wykres znajduje się powyżej osi OX, dlatego f (m) > 0 i f (n) > 0 (dla m
Wymienione powyżej warunki (1; 2; 3) są konieczne i wystarczające dla pożądanych wartości parametru.
Zadanie 7. Dla których m x2-2mx+m2-2m+5=0 nie przekracza 4 w wartości bezwzględnej?
Rozwiązanie. Warunek problemu można sformułować następująco: dla czego m jest relacją -4
Znajdujemy wartości m z systemu
D > 0; m2 - (m2 - 2m + 5) ≥ 0;
4 ≤ x0 ≤ 4; -4 ≤ m ≤ 4; f(-4)≥ 0; 16 + 8m+ m2 – 2m + 5 ≥ 0; f(4)≥0; 16-8m + m2-2m + 5 ≥0; rozwiązaniem którego jest segment . Odpowiedź: m.
Problem 8. Dla jakich wartości m są pierwiastki trójmianu kwadratowego?
Czy (2m - 2)x2 + (m+1)x + 1 jest większe niż -1, ale mniejsze niż 0?
Rozwiązanie. Wartości m można znaleźć z systemu
D≥0; (m+1)2-4(2m-2) ≥ 0;
(2m - 2)/(-1) > 0 (2m -2)(2m -2 -m -1 +1) > 0;
(2m-2)f(0)>0; (2m-2)>0;
Odpowiedź: m > 2.
Czwarte oświadczenie(-a)
Aby mniejszy pierwiastek trójmianu kwadratowego należał do przedziału (m; n), a większy nie należał do (m
D≥0; o(m)>0 o(n)
Wykres trójmianu kwadratowego przecina oś OX dokładnie raz w przedziale (m; n). Oznacza to, że w punktach x=m i x=n trójmian kwadratowy przyjmuje różne wartości znaków.
Zadanie 10. Dla jakich wartości parametru a do przedziału X(0;3) należy tylko mniejszy pierwiastek równania kwadratowego x2+2ax+a=0.
Rozwiązanie. Rozważmy trójmian kwadratowy y(x)=x2-2ax+a. Wykres jest parabolą. Gałęzie paraboli skierowane są do góry. Niech x1 będzie najmniejszym pierwiastkiem trójmianu kwadratowego. Według warunku problemu x1 należy do przedziału (0;3). Przedstawmy geometryczny model problemu, który spełnia warunki problemu.
Przejdźmy do systemu nierówności.
1) Zauważamy, że y(0)>0 i y(3) 0. Dlatego warunek ten nie musi być wpisywany do systemu nierówności.
Otrzymujemy więc następujący system nierówności:
Odpowiedź: a>1.8.
Czwarte stwierdzenie (b)
Aby większy pierwiastek trójmianu kwadratowego należał do przedziału (m; n), a mniejszy nie należał do (x1
D≥0; af(m) 0.
Czwarte oświadczenie (łącznie)
Komentarz. Niech problem zostanie sformułowany w następujący sposób, dla jakich wartości parametru jeden pierwiastek równania należy do przedziału (b; m), a drugi nie? Aby rozwiązać ten problem, nie jest konieczne rozróżnianie dwóch podprzypadków, odpowiedź znajduje się z nierówności f(m) f(n)
D≥0; f(m) f(n)
Zadanie 11. Dla czego m tylko jeden pierwiastek z równania x2-mx+6=0 spełnia warunek 2
Rozwiązanie. Na podstawie stwierdzenia 4(b) znajdujemy wartości m z warunku f(2)f(5) (10 – 2m)(31 – 5m) m2 - 24 = 0, czyli dla m = ±2 √6, Dla m = -2√6 x = - √6, które nie należy do przedziału (2; 5), przy m = 2√6 x =√6, które należy do przedziału (2; 5) .
Odpowiedź: m (2√6) U (5; 31/5).
Piąte stwierdzenie
Aby pierwiastki trójmianu kwadratowego spełniały relację (x1
D≥0; af(m)Problem 12. Znajdź wszystkie wartości m, dla których nierówność x2+2(m-3)x + m2-6m
Rozwiązanie. Z warunku przedział (0; 2) musi być zawarty w zbiorze rozwiązań nierówności x2 + 2(m - 3)x + m2 - 6m Na podstawie Twierdzenia 5 znajdujemy wartości m z układu nierówności f(0) ≤ 0;m2-6m ≤ 0; m f(2) ≤ 0,4 + 4(m-3) + m2-6m ≤ 0. m [-2;4], skąd m.
Odpowiedź: m.
Szóste stwierdzenie
Aby mniejszy pierwiastek trójmianu kwadratowego należał do przedziału (m1; m2), a większy do przedziału (n1; n2) (m2
D≥0; af(m1)>0; af(m2) To zdanie jest kombinacją zdań 4a i 4b. Dwie pierwsze nierówności gwarantują, że x1(m1, n1), a dwie ostatnie zapewniają, że x2(m2, n2),
Zadanie 13. Dla którego m jeden z pierwiastków równania x2 - (2m + l)x + m2 + m-2 = 0 znajduje się między liczbami 1 i 3, a drugi między liczbami 4 i 6?
Rozwiązanie. 1 sposób. Biorąc pod uwagę, że a = 1, wartości m można znaleźć z układu f(1) > 0; 1 -2m- 1+m2 + m-2 >0; m2-m-2>0 m (-∞;-1) U (2;+∞) f(3)
4(4) 0; 36-12m-6 + m2 + m-20 m (-∞;4)U (7;+∞), skąd m(2;4).
Odpowiedź: m(2; 4).
W ten sposób ustaliliśmy twierdzenia dotyczące położenia pierwiastków trójmianu kwadratowego f(x)=ax2+bx+ na prostej rzeczywistej względem niektórych punktów.
Wniosek
W trakcie pracy opanowałem szereg umiejętności technicznych i matematycznych na poziomie ich swobodnego wykorzystania oraz poprawiłem swoją kulturę matematyczną w ramach szkolnego kursu matematyki.
W wyniku prac osiągnięto cel: ustalono właściwości funkcji kwadratowej, które pozwalają znacznie uprościć rozwiązywanie problemów związanych z lokalizacją pierwiastków równania kwadratowego względem niektórych punktów charakterystycznych. Ustalono możliwe przypadki położenia pierwiastków trójmianu kwadratowego na prostej rzeczywistej. Zidentyfikowano algorytmy umożliwiające rozwiązywanie równań kwadratowych z parametrem opartym na położeniu pierwiastków trójmianu kwadratowego na prostej; rozwiązano zadania o większej złożoności w porównaniu z poziomem obowiązkowym. W pracy przedstawiono rozwiązanie tylko 12 problemów ze względu na ograniczoną liczbę stron pracy. Oczywiście problemy rozważane w pracy można rozwiązać w inny sposób: korzystając ze wzorów pierwiastków równania kwadratowego, stosując właściwość pierwiastka (twierdzenie Viety).
W rzeczywistości znaczna liczba zadań została rozwiązana. Dlatego postanowiono stworzyć zbiór zadań na temat pracy projektowej i badawczej „Rozwiązywanie problemów do zastosowania właściwości trójmianu kwadratowego związanego z położeniem jego pierwiastków na linii współrzędnych”. Ponadto efektem pracy (wytwór pracy projektowej i badawczej) jest prezentacja komputerowa, którą można wykorzystać na zajęciach z przedmiotu obieralnego „Rozwiązywanie problemów za pomocą parametrów”.
Temat „Trójmian kwadratowy i jego pierwiastki” jest omawiany na kursie algebry w 9 klasie. jak każda inna lekcja matematyki, lekcja na ten temat wymaga specjalnych narzędzi i metod nauczania. Widoczność jest potrzebna. Obejmuje to lekcję wideo, która została zaprojektowana specjalnie w celu ułatwienia pracy nauczyciela.
Ta lekcja trwa 6:36 minut. W tym czasie autorowi udaje się całkowicie ujawnić temat. Nauczyciel będzie musiał jedynie wybrać zadania na dany temat w celu utrwalenia materiału.
Lekcja zaczyna się od pokazania przykładów wielomianów w jednej zmiennej. Następnie na ekranie pojawia się definicja pierwiastka wielomianu. Ta definicja jest poparta przykładem, w którym konieczne jest znalezienie pierwiastków wielomianu. Po rozwiązaniu równania autor otrzymuje pierwiastki wielomianu.
Po tym następuje uwaga, że trójmiany kwadratowe obejmują również takie wielomiany drugiego stopnia, w których drugi, trzeci lub oba współczynniki, z wyjątkiem najwyższego, są równe zero. Ta informacja jest poparta przykładem, w którym wolny czynnik wynosi zero.
Autor następnie wyjaśnia, jak znaleźć pierwiastki trójmianu kwadratowego. Aby to zrobić, musisz rozwiązać równanie kwadratowe. A autor sugeruje sprawdzenie tego na przykładzie, w którym podano trójmian kwadratowy. Musimy znaleźć jego korzenie. Rozwiązanie jest budowane na podstawie rozwiązania równania kwadratowego otrzymanego z danego trójmianu kwadratowego. Rozwiązanie jest szczegółowo wypisane na ekranie, w sposób jasny i zrozumiały. W trakcie rozwiązywania tego przykładu autor zapamiętuje sposób rozwiązania równania kwadratowego, zapisuje wzory i otrzymuje wynik. Odpowiedź jest napisana na ekranie.
Autor wyjaśnił znalezienie pierwiastków trójmianu kwadratowego na przykładzie. Kiedy uczniowie zrozumieją istotę, możesz przejść do bardziej ogólnych punktów, co robi autor. Dlatego dalej podsumowuje wszystkie powyższe. Ogólnie rzecz biorąc, w języku matematycznym autor zapisuje zasadę znajdowania pierwiastków trójmianu kwadratowego.
Z uwagi wynika, że w niektórych problemach wygodniej jest zapisać trójmian kwadratowy w nieco inny sposób. Ten wpis jest wyświetlany na ekranie. Oznacza to, że okazuje się, że kwadrat dwumianu można odróżnić od trójmianu kwadratu. Proponuje się rozważenie takiej transformacji na przykładzie. Rozwiązanie tego przykładu jest pokazane na ekranie. Podobnie jak w poprzednim przykładzie, rozwiązanie jest szczegółowo zbudowane ze wszystkimi niezbędnymi wyjaśnieniami. Następnie autor rozważa problem, w którym wykorzystano podane przed chwilą informacje. To jest problem z dowodem geometrycznym. Rozwiązanie zawiera ilustrację w formie rysunku. Rozwiązanie problemu jest szczegółowe i jasne.
To kończy lekcję. Ale nauczyciel może wybrać, zgodnie z umiejętnościami uczniów, zadania, które będą odpowiadać temu tematowi.
Ta lekcja wideo może być wykorzystana jako wyjaśnienie nowego materiału na lekcjach algebry. Jest idealny do samokształcenie uczniów na lekcję.
