Wprowadzony przez nas operacje liniowe na wektorach umożliwiają tworzenie różnych wyrażeń wielkości wektorowe i przekształcaj je, korzystając z właściwości ustawionych dla tych operacji.
Na podstawie danego zbioru wektorów a 1, ..., a n można utworzyć wyrażenie postaci
gdzie a 1, ... i n są dowolnymi liczbami rzeczywistymi. To wyrażenie nazywa się liniowa kombinacja wektorów a 1, ..., n. Liczby α i, i = 1, n reprezentują współczynniki kombinacji liniowej. Zbiór wektorów nazywany jest również układ wektorów.
W związku z wprowadzoną koncepcją kombinacji liniowej wektorów pojawia się problem opisania zbioru wektorów, który można zapisać jako kombinację liniową danego układu wektorów a 1, ..., a n. Poza tym naturalne są pytania o warunki, w jakich istnieje reprezentacja wektora w postaci kombinacji liniowej oraz o jednoznaczność takiej reprezentacji.
Definicja 2.1. Nazywa się wektory a 1, ... i n liniowo zależne, jeśli istnieje zbiór współczynników α 1 , ... , α n taki, że
α 1 za 1 + ... + α n а n = 0 (2.2)
i co najmniej jeden z tych współczynników jest niezerowy. Jeśli określony zbiór współczynników nie istnieje, wywoływane są wektory liniowo niezależny.
Jeśli α 1 = ... = α n = 0, to oczywiście α 1 a 1 + ... + α n a n = 0. Mając to na uwadze, możemy powiedzieć tak: wektory a 1, ... i n są liniowo niezależne, jeżeli z równości (2.2) wynika, że wszystkie współczynniki α 1 , ... , α n są równe zeru.
Poniższe twierdzenie wyjaśnia, dlaczego nowe pojęcie nosi nazwę „zależność” (lub „niezależność”) i dostarcza prostego kryterium zależności liniowej.
Twierdzenie 2.1. Aby wektory a 1, ... i n, n > 1 były liniowo zależne, konieczne i wystarczające jest, aby jeden z nich był liniową kombinacją pozostałych.
◄ Konieczność. Załóżmy, że wektory a 1, ... i n są liniowo zależne. Zgodnie z definicją 2.1 zależności liniowej, w równości (2.2) po lewej stronie znajduje się co najmniej jeden niezerowy współczynnik, np. α 1. Pozostawiając pierwszy wyraz po lewej stronie równości, resztę przesuwamy na prawą stronę, jak zwykle zmieniając ich znaki. Dzieląc wynikową równość przez α 1, otrzymujemy
za 1 =-α 2 /α 1 ⋅ za 2 - ... - α n /α 1 ⋅ za n
te. reprezentacja wektora a 1 jako kombinacja liniowa pozostałych wektorów a 2, ..., an.
Adekwatność. Niech na przykład pierwszy wektor a 1 można przedstawić jako kombinację liniową pozostałych wektorów: a 1 = β 2 a 2 + ... + β n a n. Przenosząc wszystkie wyrazy z prawej strony na lewą, otrzymujemy a 1 - β 2 a 2 - ... - β n a n = 0, tj. liniowa kombinacja wektorów a 1, ..., an o współczynnikach α 1 = 1, α 2 = - β 2, ..., α n = - β n, równe wektor zerowy. W tej kombinacji liniowej nie wszystkie współczynniki wynoszą zero. Zgodnie z definicją 2.1 wektory a 1, ... i n są liniowo zależne.
Definicja i kryterium zależności liniowej są sformułowane tak, aby sugerować obecność dwóch lub więcej wektorów. Można jednak mówić także o liniowej zależności jednego wektora. Aby zrealizować tę możliwość, zamiast „wektory są liniowo zależne”, należy powiedzieć „układ wektorów jest liniowo zależny”. Łatwo zauważyć, że wyrażenie „układ jednego wektora jest liniowo zależny” oznacza, że ten pojedynczy wektor ma wartość zero (w kombinacji liniowej występuje tylko jeden współczynnik i nie powinien on być równy zero).
Pojęcie zależności liniowej ma prostą interpretację geometryczną. Poniższe trzy stwierdzenia wyjaśniają tę interpretację.
Twierdzenie 2.2. Dwa wektory są liniowo zależne wtedy i tylko wtedy, gdy współliniowy.
◄ Jeśli wektory a i b są liniowo zależne, to jeden z nich, na przykład a, wyraża się przez drugi, tj. a = λb dla pewnej liczby rzeczywistej λ. Zgodnie z definicją 1.7 Pracuje wektory na liczbę, wektory aib są współliniowe.
Niech teraz wektory aib będą współliniowe. Jeśli oba mają wartość zerową, to oczywiste jest, że są one liniowo zależne, ponieważ jakakolwiek ich kombinacja liniowa jest równa wektorowi zerowemu. Niech jeden z tych wektorów nie będzie równy 0, na przykład wektor b. Oznaczmy przez λ stosunek długości wektorów: λ = |a|/|b|. Mogą być wektory współliniowe jednokierunkowy Lub skierowane przeciwnie. W tym drugim przypadku zmieniamy znak λ. Następnie sprawdzając Definicję 1.7, jesteśmy przekonani, że a = λb. Zgodnie z Twierdzeniem 2.1 wektory aib są liniowo zależne.
Uwaga 2.1. W przypadku dwóch wektorów, biorąc pod uwagę kryterium zależności liniowej, sprawdzone twierdzenie można przeformułować w następujący sposób: dwa wektory są współliniowe wtedy i tylko wtedy, gdy jeden z nich jest przedstawiony jako iloczyn drugiego przez liczbę. Jest to wygodne kryterium kolinearności dwóch wektorów.
Twierdzenie 2.3. Trzy wektory są liniowo zależne wtedy i tylko wtedy, gdy współpłaszczyznowy.
◄ Jeżeli trzy wektory a, b, c są liniowo zależne, to zgodnie z Twierdzeniem 2.1 jeden z nich, np. a, jest liniową kombinacją pozostałych: a = βb + γс. Połączmy początki wektorów b i c w punkcie A. Wtedy wektory βb, γс będą miały wspólny początek w punkcie A i wzdłuż zgodnie z zasadą równoległoboku ich suma wynosi te. wektor a będzie wektorem o początku A i koniec, który jest wierzchołkiem równoległoboku zbudowanego na wektorach składowych. Zatem wszystkie wektory leżą w tej samej płaszczyźnie, tj. Współpłaszczyznowej.
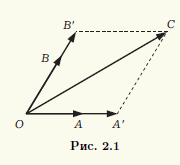
Niech wektory a, b, c będą współpłaszczyznowe. Jeśli jeden z tych wektorów ma wartość zero, to będzie to oczywiście kombinacja liniowa pozostałych. Wystarczy przyjąć wszystkie współczynniki kombinacji liniowej równe zero. Dlatego możemy założyć, że wszystkie trzy wektory nie są zerowe. Zgodny Rozpoczęty tych wektorów w wspólnym punkcie O. Niech ich końcami będą odpowiednio punkty A, B, C (ryc. 2.1). Przez punkt C rysujemy proste równoległe do prostych przechodzących przez pary punktów O, A i O, B. Wyznaczając punkty przecięcia jako A” i B”, otrzymujemy równoległobok OA”CB”, zatem OC” = OA” + OB". Wektor OA" i niezerowy wektor a = OA są współliniowe, dlatego pierwszy z nich można otrzymać mnożąc drugi przez liczbę rzeczywistą α:OA" = αOA. Podobnie OB" = βOB, β ∈ R. Otrzymujemy, że OC" = α OA + βOB, czyli wektor c jest liniową kombinacją wektorów a i b. Zgodnie z Twierdzeniem 2.1 wektory a, b, c są liniowo zależne.
Twierdzenie 2.4. Dowolne cztery wektory są liniowo zależne.
◄ Dowód przeprowadzamy według tego samego schematu, co w Twierdzeniu 2.3. Rozważmy dowolne cztery wektory a, b, cid. Jeśli jeden z czterech wektorów ma wartość zero lub są wśród nich dwa wektory współliniowe lub trzy z czterech wektorów są współpłaszczyznowe, wówczas te cztery wektory są liniowo zależne. Na przykład, jeśli wektory aib są współliniowe, to możemy utworzyć ich kombinację liniową αa + βb = 0 z niezerowymi współczynnikami, a następnie dodać pozostałe dwa wektory do tej kombinacji, przyjmując zera jako współczynniki. Otrzymujemy kombinację liniową czterech wektorów równych 0, w których występują niezerowe współczynniki.
Możemy zatem założyć, że spośród wybranych czterech wektorów żaden wektor nie jest zerowy, żadne dwa nie są współliniowe i żadne trzy nie są współpłaszczyznowe. Jako ich wspólny początek wybierzmy punkt O. Wtedy końcami wektorów a, b, c, d będą punkty A, B, C, D (rys. 2.2). Przez punkt D rysujemy trzy płaszczyzny, równolegle do płaszczyzn OBC, OCA, OAB i niech A", B", C" będą punktami przecięcia tych płaszczyzn z prostymi odpowiednio OA, OB, OS. Otrzymujemy równoległościan OA"C"B"C"B"DA ", a wektory a, b, c leżą na jego krawędziach wychodzących z wierzchołka O. Ponieważ czworokąt OC"DC" jest równoległobokiem, to OD = OC" + OC". Z kolei odcinek OC" jest przekątną równoległobok OA"C"B", tak że OC" = OA" + OB" i OD = OA" + OB" + OC" .
Pozostaje zauważyć, że pary wektorów OA ≠ 0 i OA" , OB ≠ 0 i OB" , OC ≠ 0 i OC" są współliniowe, dlatego można tak dobrać współczynniki α, β, γ, że OA" = αOA, OB" = βOB i OC" = γOC. W końcu otrzymujemy OD = αOA + βOB + γOC. W konsekwencji wektor OD jest wyrażany przez pozostałe trzy wektory, a wszystkie cztery wektory, zgodnie z Twierdzeniem 2.1, są liniowo zależne.
Definicja. Liniowa kombinacja wektorów a 1 , ..., an o współczynnikach x 1 , ..., x n nazywa się wektorem
x 1 za 1 + ... + x n za n .
trywialny, jeśli wszystkie współczynniki x 1 , ..., x n są równe zero.
Definicja. Nazywa się kombinację liniową x 1 a 1 + ... + x n a n nietrywialne, jeśli przynajmniej jeden ze współczynników x 1, ..., x n nie jest równy zero.
liniowo niezależny, jeśli nie ma nietrywialnej kombinacji tych wektorów równej wektorowi zerowemu.
Oznacza to, że wektory a 1, ..., a n są liniowo niezależne, jeśli x 1 a 1 + ... + x n a n = 0 wtedy i tylko wtedy, gdy x 1 = 0, ..., x n = 0.
Definicja. Nazywa się wektory a 1, ..., an liniowo zależne, jeśli istnieje nietrywialna kombinacja tych wektorów równa wektorowi zerowemu.
Własności wektorów liniowo zależnych:
Dla wektorów n-wymiarowych.
wektory n + 1 są zawsze liniowo zależne.
Dla wektorów 2 i 3 wymiarowych.
Dwa liniowo zależne wektory są współliniowe. (Wektory współliniowe są liniowo zależne.)
Dla wektorów trójwymiarowych.
Trzy liniowo zależne wektory są współpłaszczyznowe. (Trzy wektory współpłaszczyznowe są liniowo zależne.)
Przykładowe problemy liniowej zależności i liniowej niezależności wektorów:
Przykład 1. Sprawdź, czy wektory a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) są liniowo niezależne .
Rozwiązanie:
Wektory będą liniowo zależne, ponieważ wymiar wektorów jest mniejszy niż liczba wektorów.
Przykład 2. Sprawdź, czy wektory a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) są liniowo niezależne.
Rozwiązanie:
| x 1 + x 2 = 0 | |
| x 1 + 2 x 2 - x 3 = 0 | |
| x 1 + x 3 = 0 |
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 1 | 0 |
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 1 - 0 | 0 - 0 | 0 | -1 | 1 | 0 |
odejmij drugą od pierwszej linii; dodaj drugą linię do trzeciej linii:
| ~ | 1 - 0 | 1 - 1 | 0 - (-1) | 0 - 0 | ~ | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 + 0 | 0 | 0 | 0 | 0 |
Rozwiązanie to pokazuje, że układ ma wiele rozwiązań, czyli istnieje niezerowa kombinacja wartości liczb x 1, x 2, x 3 taka, że kombinacja liniowa wektorów a, b, c jest równa wektor zerowy, na przykład:
A + b + do = 0
co oznacza, że wektory a, b, c są liniowo zależne.
Odpowiedź: wektory a, b, c są liniowo zależne.
Przykład 3. Sprawdź, czy wektory a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) są liniowo niezależne.
Rozwiązanie: Znajdźmy wartości współczynników, przy których kombinacja liniowa tych wektorów będzie równa wektorowi zerowemu.
x 1 za + x 2 b + x 3 do 1 = 0To równanie wektorowe można zapisać w postaci układu równania liniowe
| x 1 + x 2 = 0 | |
| x 1 + 2 x 2 - x 3 = 0 | |
| x 1 + 2 x 3 = 0 |
Rozwiążmy ten układ metodą Gaussa
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 2 | 0 |
odejmij pierwszą od drugiej linii; odejmij pierwszą od trzeciej linii:
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 2 - 0 | 0 - 0 | 0 | -1 | 2 | 0 |
odejmij drugą od pierwszej linii; dodaj drugą do trzeciej linii.
Pozwalać L jest dowolną przestrzenią liniową, a I Î L,- jego elementy (wektory).
Definicja 3.3.1. Wyrażenie , Gdzie , - dowolne liczby rzeczywiste, zwane kombinacją liniową wektory a 1 , a 2 ,…, a N.
Jeśli wektor R = , wtedy tak mówią R rozłożone na wektory a 1 , a 2 ,…, a N.
Definicja 3.3.2. Nazywa się liniową kombinacją wektorów nietrywialne, jeśli wśród liczb jest przynajmniej jedna liczba różna od zera. W przeciwnym razie wywoływana jest kombinacja liniowa trywialny.
Definicja 3.3.3 . Wektory a 1 , a 2 ,…, a N nazywane są liniowo zależnymi, jeśli istnieje ich nietrywialna kombinacja liniowa taka, że
= 0 .
Definicja 3.3.4. Wektory a 1 , a 2 ,…, a N nazywane są liniowo niezależnymi, jeśli równość = 0 jest możliwe tylko w przypadku, gdy wszystkie liczby l 1, l 2,…, l n są jednocześnie równe zeru.
Należy zauważyć, że każdy niezerowy element a 1 można uznać za układ liniowo niezależny, ponieważ zachodzi równość l 1 = 0 możliwe tylko wtedy, gdy l= 0.
Twierdzenie 3.3.1. Warunek konieczny i wystarczający zależności liniowej a 1 , a 2 ,…, a N jest możliwością rozłożenia przynajmniej jednego z tych elementów na resztę.
Dowód. Konieczność. Niech elementy a 1 , a 2 ,…, a N liniowo zależne. To znaczy, że = 0 i co najmniej jedną z liczb l 1, l 2,…, l n różny od zera. Niech będzie pewność l 1 ¹ 0. Następnie
tj. element a 1 jest rozkładany na elementy a 2 , a 3 , …, a N.
Adekwatność. Niech element a 1 zostanie rozłożony na elementy a 2 , a 3 , …, a N, tj. 1 = . Następnie 
= 0
, zatem istnieje nietrywialna kombinacja liniowa wektorów a 1 , a 2 ,…, a N, równy 0
, więc są liniowo zależne .
Twierdzenie 3.3.2. Jeżeli przynajmniej jeden z elementów a 1 , a 2 ,…, a N zero, to wektory te są liniowo zależne.
Dowód . Pozwalać A N= 0 , wtedy = 0 , co oznacza liniową zależność tych elementów.
Twierdzenie 3.3.3. Jeśli spośród n wektorów dowolne p (str< n) векторов линейно зависимы, то и все n элементов линейно зависимы.
Dowód. Niech dla określoności elementy a 1 , a 2 ,…, a P liniowo zależne. Oznacza to, że istnieje nietrywialna kombinacja liniowa taka, że = 0 . Podana równość zostanie zachowana, jeśli dodamy element do obu jego części. Następnie + = 0 i co najmniej jedną z liczb l 1, l 2,…, lp różny od zera. Zatem wektory a 1 , a 2 ,…, a N są liniowo zależne.
Wniosek 3.3.1. Jeżeli n elementów jest liniowo niezależnych, to dowolne k z nich jest liniowo niezależne (k< n).
Twierdzenie 3.3.4. Jeśli wektory a 1 , a 2 ,…, a N- 1 są liniowo niezależne, oraz elementy a 1 , a 2 ,…, a N- 1, za n są liniowo zależne, to wektor A n można rozwinąć na wektory a 1 , a 2 ,…, a N- 1 .
Dowód. Ponieważ według warunku a 1 , a 2 ,…,A N- 1, za N są liniowo zależne, to istnieje ich nietrywialna kombinacja liniowa = 0 , i (w przeciwnym razie okażą się liniowe wektory zależne a 1 , a 2 ,…, a N- 1). Ale potem wektor
,
co było do okazania
Nazywa się układ wektorów liniowo zależne, jeśli istnieją liczby, spośród których co najmniej jedna jest różna od zera, tak że równość https://pandia.ru/text/78/624/images/image004_77.gif" szerokość="57" wysokość="24 src= " >.
Jeżeli równość ta jest spełniona tylko w przypadku, gdy wszystkie , to wywoływany jest układ wektorów liniowo niezależny.
Twierdzenie. System wektorowy będzie liniowo zależne wtedy i tylko wtedy, gdy co najmniej jeden z jego wektorów jest kombinacją liniową pozostałych.
Przykład 1. Wielomian 
jest liniową kombinacją wielomianów https://pandia.ru/text/78/624/images/image010_46.gif" szerokość="88 wysokość=24" wysokość="24">. Wielomiany stanowią układ liniowo niezależny, ponieważ wielomian https: //pandia.ru/text/78/624/images/image012_44.gif" szerokość="129" wysokość="24">.
Przykład 2. System macierzowy, https://pandia.ru/text/78/624/images/image016_37.gif" szerokość="51" wysokość="48 src="> jest liniowo niezależny, ponieważ kombinacja liniowa jest równa macierz zerowa tylko w przypadku, gdy https://pandia.ru/text/78/624/images/image019_27.gif" szerokość="69" height="21">, , https://pandia.ru/text /78/624 /images/image022_26.gif" szerokość="40" wysokość="21"> zależna liniowo.
Rozwiązanie.
Zróbmy kombinację liniową tych wektorów https://pandia.ru/text/78/624/images/image023_29.gif" szerokość="97" wysokość="24">=0..gif" szerokość="360" wysokość=" 22">.
Przyrównując te same współrzędne równych wektorów, otrzymujemy https://pandia.ru/text/78/624/images/image027_24.gif" szerokość="289" wysokość="69">
Wreszcie dostajemy
I
Układ ma unikalne rozwiązanie trywialne, więc kombinacja liniowa tych wektorów jest równa zero tylko w przypadku, gdy wszystkie współczynniki są równe zero. Dlatego ten układ wektorów jest liniowo niezależny.
Przykład 4. Wektory są liniowo niezależne. Jakie będą systemy wektorowe?
A).
;
B).
?
Rozwiązanie.
A). Zróbmy kombinację liniową i przyrównajmy ją do zera
Korzystając z własności operacji na wektorach w przestrzeni liniowej, przepisujemy ostatnią równość w postaci
Ponieważ wektory są liniowo niezależne, współczynniki at muszą być równe zeru, tj..gif" szerokość="12" wysokość="23 src=">
Powstały układ równań ma unikalne, trywialne rozwiązanie 
.
Od równości (*) wykonywany tylko wtedy, gdy https://pandia.ru/text/78/624/images/image031_26.gif" szerokość="115 wysokość=20" wysokość="20"> – liniowo niezależny;
B). Zróbmy równość https://pandia.ru/text/78/624/images/image039_17.gif" szerokość="265" wysokość="24 src="> (**)
Stosując podobne rozumowanie, otrzymujemy
Rozwiązując układ równań metodą Gaussa, otrzymujemy
Lub
Ten ostatni system ma nieskończoną liczbę rozwiązań https://pandia.ru/text/78/624/images/image044_14.gif" szerokość="149" wysokość="24 src=">. Zatem istnieje nie- zerowy zbiór współczynników, dla którego zachodzi równość (**)
. Dlatego układ wektorów – liniowo zależny.
Przykład 5 Układ wektorów jest liniowo niezależny, a układ wektorów jest liniowo zależny..gif" szerokość="80" wysokość="24">.gif" szerokość="149 wysokość=24" wysokość="24"> (***)
W równości (***) . Rzeczywiście, w , system byłby liniowo zależny.
Z relacji (***)
dostajemy 
Lub 
Oznaczmy 
.
Dostajemy 
Zadania dla niezależna decyzja(wśród publiczności)
1. Układ zawierający wektor zerowy jest liniowo zależny.
2. Układ składający się z jednego wektora A, jest liniowo zależna wtedy i tylko wtedy, gdy, a=0.
3. Układ składający się z dwóch wektorów jest liniowo zależny wtedy i tylko wtedy, gdy wektory są proporcjonalne (to znaczy jeden z nich otrzymuje się z drugiego przez pomnożenie przez liczbę).
4. Jeśli dodasz wektor do układu liniowo zależnego, otrzymasz układ liniowo zależny.
5. Jeśli wektor zostanie usunięty z układu liniowo niezależnego, wówczas powstały układ wektorów będzie liniowo niezależny.
6. Jeśli systemu S jest liniowo niezależny, ale staje się liniowo zależny po dodaniu wektora B, następnie wektor B wyrażone liniowo poprzez wektory systemowe S.
C). Układ macierzy , , w przestrzeni macierzy drugiego rzędu.
10. Niech układ wektorów A,B,C przestrzeń wektorowa jest liniowo niezależna. Udowodnić liniową niezależność następujących układów wektorowych:
A).+b, b, c.
B).+https://pandia.ru/text/78/624/images/image062_13.gif" szerokość="15" wysokość="19">– dowolna liczba
C).+b, a+c, b+c.
11. Pozwalać A,B,C– trzy wektory na płaszczyźnie, z których można utworzyć trójkąt. Czy te wektory będą liniowo zależne?
12. Podano dwa wektory a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). Znajdź dwa kolejne czterowymiarowe wektory a3 ia4 tak, że system a1,a2,a3,a4 był liniowo niezależny .
Zadanie 1. Sprawdź, czy układ wektorów jest liniowo niezależny. Układ wektorów będzie określony przez macierz układu, której kolumny składają się ze współrzędnych wektorów.
.
Rozwiązanie. Niech kombinacja liniowa 
równy zeru. Po zapisaniu tej równości we współrzędnych otrzymujemy następujący układ równań:
.
Taki układ równań nazywa się trójkątnym. Ona ma tylko jedno rozwiązanie 
. Dlatego wektory 
liniowo niezależny.
Zadanie 2. Sprawdź, czy układ wektorów jest liniowo niezależny.
.
Rozwiązanie. Wektory 
są liniowo niezależne (patrz zadanie 1). Udowodnijmy, że wektor jest liniową kombinacją wektorów 
. Współczynniki rozszerzalności wektora 
wyznaczane są z układu równań
.
System ten, podobnie jak trójkątny, posiada unikalne rozwiązanie.
Dlatego układ wektorów 
liniowo zależne.
Komentarz. Nazywa się macierze tego samego typu co w Zadaniu 1 trójkątny , a w zadaniu 2 – schodkowy trójkątny . Zagadnienie liniowej zależności układu wektorów można łatwo rozwiązać, jeśli macierz złożona ze współrzędnych tych wektorów jest trójkątem schodkowym. Jeśli matryca nie ma specjalny typ, a następnie za pomocą konwersje ciągów elementarnych , zachowując liniowe zależności między kolumnami, można je sprowadzić do postaci trójkąta schodkowego.
Podstawowe konwersje ciągów nazywane są matrycami (EPS). kolejne operacje nad macierzą:
1) przegrupowanie linii;
2) pomnożenie ciągu przez liczbę niezerową;
3) dodanie kolejnego ciągu do ciągu pomnożonego przez dowolną liczbę.
Zadanie 3. Znajdź maksymalny liniowo niezależny podsystem i oblicz rząd układu wektorów
.
Rozwiązanie. Zredukujmy macierz układu za pomocą EPS do postaci trójkąta schodkowego. Aby wyjaśnić procedurę, oznaczamy linię z numerem macierzy, która ma zostać przekształcona przez symbol . Kolumna za strzałką wskazuje działania na wierszach konwertowanej macierzy, które należy wykonać, aby otrzymać wiersze nowej macierzy.
.
Oczywiście dwie pierwsze kolumny wynikowej macierzy są liniowo niezależne, trzecia kolumna jest ich liniową kombinacją, a czwarta nie zależy od pierwszych dwóch. Wektory 
nazywane są podstawowymi. Tworzą maksymalnie liniowo niezależny podsystem systemu , a ranga systemu wynosi trzy.
Podstawa, współrzędne
Zadanie 4. Znajdź bazę i współrzędne wektorów z tej bazy na zbiorze wektorów geometrycznych, których współrzędne spełniają warunek 
.
Rozwiązanie. Zbiór jest płaszczyzną przechodzącą przez początek układu współrzędnych. Dowolna baza na płaszczyźnie składa się z dwóch niewspółliniowych wektorów. Współrzędne wektorów w wybranej bazie wyznacza się rozwiązując odpowiedni układ równań liniowych.
Istnieje inny sposób rozwiązania tego problemu, polegający na znalezieniu podstawy za pomocą współrzędnych.
Współrzędne 
przestrzenie nie są współrzędnymi na płaszczyźnie, ponieważ są ze sobą powiązane relacją 
, to znaczy, że nie są niezależne. Zmienne niezależne i (nazywane są wolnymi) jednoznacznie definiują wektor na płaszczyźnie i dlatego można je wybrać jako współrzędne w . Następnie podstawa 
składa się z wektorów leżących w zbiorach wolnych zmiennych i odpowiadających im 
I 
, to jest .
Zadanie 5. Znajdź bazę i współrzędne wektorów na tej podstawie na zbiorze wszystkich wektorów w przestrzeni, których współrzędne nieparzyste są sobie równe.
Rozwiązanie. Wybierzmy, podobnie jak w poprzednim zadaniu, współrzędne w przestrzeni.
Ponieważ 
, a następnie wolne zmienne 
jednoznacznie określają wektor z i dlatego są współrzędnymi. Odpowiednia baza składa się z wektorów.
Zadanie 6. Znajdź bazę i współrzędne wektorów na tej podstawie na zbiorze wszystkich macierzy postaci 
, Gdzie 
– liczby dowolne.
Rozwiązanie. Każda macierz jest jednoznacznie reprezentowana w postaci:
Relacja ta jest rozwinięciem wektora względem podstawy 
ze współrzędnymi 
.
Zadanie 7. Znajdź wymiar i podstawę liniowego kadłuba układu wektorów
.
Rozwiązanie. Korzystając z EPS, przekształcamy macierz ze współrzędnych wektorów układu do postaci trójkąta schodkowego.
.
Kolumny 
ostatnie macierze są liniowo niezależne, a kolumny 
wyrażane poprzez nie liniowo. Dlatego wektory 
stanowić podstawę 
, I 
.
Komentarz. Podstawa w jest wybrany niejednoznacznie. Na przykład wektory 
stanowią również podstawę 
.
