W tym artykule przyjrzymy się całościowo. Podstawowe tożsamości trygonometryczne to równości, które ustanawiają połączenie między sinusem, cosinusem, styczną i cotangensem jednego kąta i pozwalają znaleźć dowolną z tych funkcji trygonometrycznych poprzez znaną inną.
Wymieńmy od razu główne tożsamości trygonometryczne, które przeanalizujemy w tym artykule. Zapiszmy je w tabeli, a poniżej podamy wynik tych wzorów i podamy niezbędne wyjaśnienia.
Nawigacja strony.
Zależność między sinusem i cosinusem jednego kąta
Czasami nie mówią o głównych tożsamościach trygonometrycznych wymienionych w powyższej tabeli, ale o jednej podstawowa tożsamość trygonometryczna Uprzejmy 
. Wyjaśnienie tego faktu jest dość proste: równości otrzymuje się z głównej tożsamości trygonometrycznej po podzieleniu obu jej części odpowiednio przez i oraz równości 
I 
wynikają z definicji sinusa, cosinusa, tangensa i cotangensa. Porozmawiamy o tym bardziej szczegółowo w kolejnych akapitach.
Oznacza to, że szczególnie interesująca jest równość, której nadano nazwę głównej tożsamości trygonometrycznej.
Zanim udowodnimy główną tożsamość trygonometryczną, podajemy jej sformułowanie: suma kwadratów sinusa i cosinusa jednego kąta jest identyczna równa jeden. Teraz udowodnijmy to.
Podstawowa tożsamość trygonometryczna jest bardzo często używana, gdy konwertowanie wyrażeń trygonometrycznych. Umożliwia zastąpienie sumy kwadratów sinusa i cosinusa jednego kąta przez jeden. Nie mniej często podstawową tożsamość trygonometryczną stosuje się w odwrotnej kolejności: jednostkę zastępuje się sumą kwadratów sinusa i cosinusa dowolnego kąta.
Tangens i cotangens przez sinus i cosinus
Tożsamości łączące styczną i cotangens z sinusem i cosinusem jednego kąta widzenia i 
wynikają bezpośrednio z definicji sinusa, cosinusa, tangensa i cotangensa. Rzeczywiście, z definicji sinus jest rzędną y, cosinus jest odciętą x, tangens jest stosunkiem rzędnej do odciętej, to znaczy: 
, a cotangens jest stosunkiem odciętej do rzędnej, to znaczy 
.
Dzięki takiej oczywistości tożsamości i Styczna i cotangens są często definiowane nie poprzez stosunek odciętej i rzędnej, ale poprzez stosunek sinusa i cosinusa. Zatem tangens kąta to stosunek sinusa do cosinusa tego kąta, a cotangens to stosunek cosinusa do sinusa.
Podsumowując ten akapit, należy zauważyć, że tożsamości i zachodzą dla wszystkich kątów, przy których zawarte w nich funkcje trygonometryczne mają sens. Zatem wzór obowiązuje dla dowolnego , innego niż (w przeciwnym razie w mianowniku będzie zero, a nie zdefiniowaliśmy dzielenia przez zero), a wzór - dla wszystkich, różne od , gdzie z jest dowolne.
Zależność między styczną i kotangensem
Jeszcze bardziej oczywistą tożsamością trygonometryczną niż dwie poprzednie jest tożsamość łącząca styczną i cotangens jednego kąta formy . Jest oczywiste, że dotyczy to dowolnych kątów innych niż , w przeciwnym razie ani styczna, ani cotangens nie są zdefiniowane.
Dowód wzoru bardzo prosta. Z definicji i skąd 
. Dowód można było przeprowadzić nieco inaczej. Od , To 
.
Zatem tangens i cotangens tego samego kąta, dla którego mają one sens, wynoszą .
Temat: Wzory trygonometryczne(25 godzin)
Lekcja 6 – 7: Zależność między sinusem, cosinusem i tangensem tego samego kąta.
Cel: zbadaj związek między sinusem, cosinusem i tangensem tego samego kąta. Aby osiągnąć ten cel konieczne jest:
- Wiedzieć:
- sformułowania definicji podstawowych funkcji trygonometrycznych (sinus, cosinus i tangens); znaki funkcji trygonometrycznych według ćwiartek; zbiór wartości funkcji trygonometrycznych; podstawowe wzory trygonometrii.
- Zrozumieć:
- że podstawowej tożsamości trygonometrycznej można użyć tylko dla tego samego argumentu; algorytm obliczania jednej funkcji trygonometrycznej za pomocą drugiej.
- Stosować:
- umiejętność prawidłowego wyboru właściwej formuły do rozwiązania konkretnego zadania; umiejętność pracy z ułamki proste; umiejętność wykonywania przekształceń wyrażeń trygonometrycznych.
- Analiza:
- analizować błędy w logice rozumowania.
- Synteza:
- zaproponować własny sposób rozwiązywania przykładów; utwórz krzyżówkę wykorzystując zdobytą wiedzę.
- Stopień:
- wiedzę i umiejętności na ten temat do wykorzystania w innych działach algebry.
- Organizowanie czasu.
- Aktualizowanie wiedzy i umiejętności.
- W której ćwiartce znajduje się kąt 1 radiana i ile on jest w przybliżeniu równy?
- Jakiego słowa brakuje w definicji funkcji sinus?
- Jakiego słowa brakuje w definicji funkcji cosinus?
- Jakie wartości może przyjmować sinus?
() - Wyjaśnienie nowego materiału.
Przedstawmy okrąg jednostkowy ze środkiem w punkcie O. Załóżmy, że obracając promień OA równy R o kąt , otrzymujemy promień OB (rys. 5). Wtedy z definicji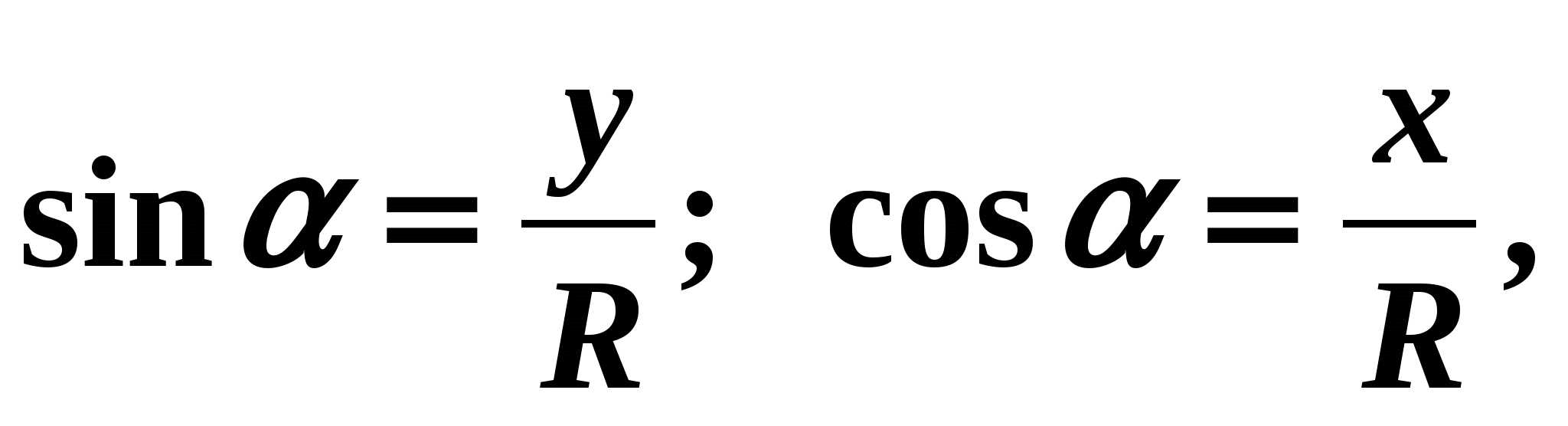 
Gdzie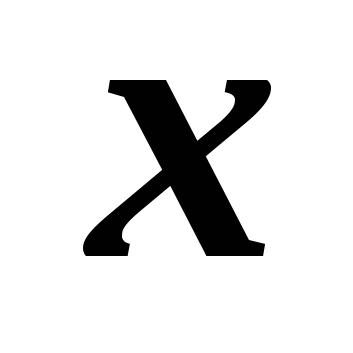 
– odcięta punktu B, 
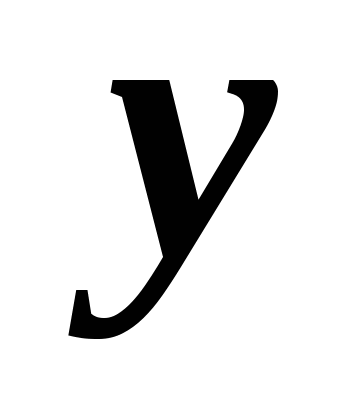– jego rzędna. Wynika z tego, że punkt B należy do okręgu. Dlatego jego współrzędne spełniają równanie 
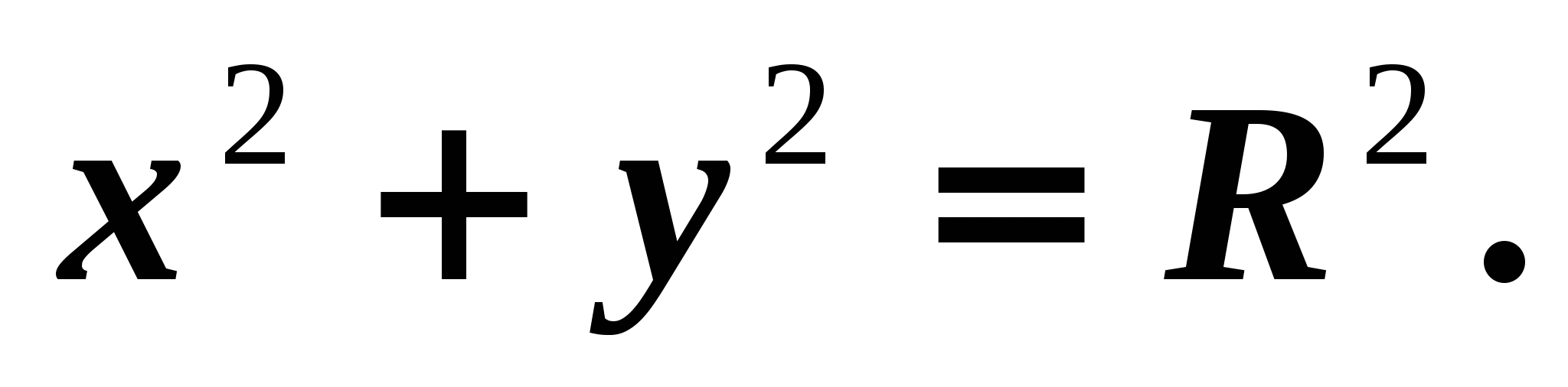Korzystamy z tego, co dostajemy 
(1).
Otrzymaliśmy równość obowiązującą dla dowolnych wartości liter w niej zawartych. Jak nazywają się takie równości? Zgadza się – tożsamości. Równość (1) nazywa się podstawowa tożsamość trygonometryczna. W równości (1) może przyjmować dowolną wartość. Dokończ nagranie samodzielnie: 1.
Sprawdź, czy Twój wpis jest poprawny. Dodaj punkty do swojej karty lekcji za Zadania nr 2. Kontynuujmy. Wyprowadziliśmy główną tożsamość trygonometryczną, ale dlaczego jej potrzebujemy? Zgadza się – znaleźć wartość cosinus na podstawie jednej znanej wartości sinusa i odwrotnie. Teraz ty i ja zawsze możemy używać podstawowej tożsamości trygonometrycznej, ale najważniejsze jest to, że ten sam argument. W zeszycie uczniowie proszeni są o samodzielne wyrażenie sinusa przez cosinus i cosinus przez sinus z podstawowej tożsamości trygonometrycznej. Dwóch uczniów zostaje wezwanych do tablicy w celu sprawdzenia. Jeden proszony jest o wyrażenie sinusa przez cosinus, drugi - cosinus przez sinus. Prawidłowa odpowiedź zostanie wyświetlona na ekranie:
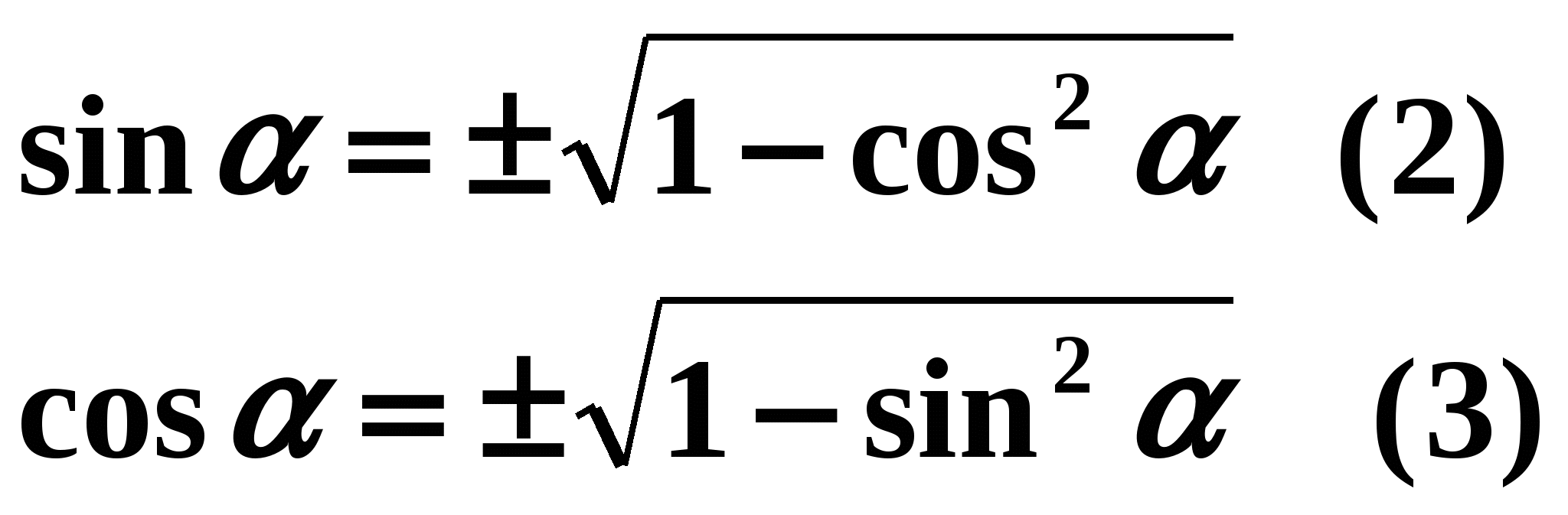Uczniowie sprawdzają swoje odpowiedzi i dodają punkty do karty lekcji Zadania nr 3.
Od czego w tych wzorach zależy znak przed pierwiastkiem? (Zależy to od tego, w której ćwiartce znajduje się kąt funkcji trygonometrycznej, którą definiujemy). Przykład 1 . Oblicz
Jeśli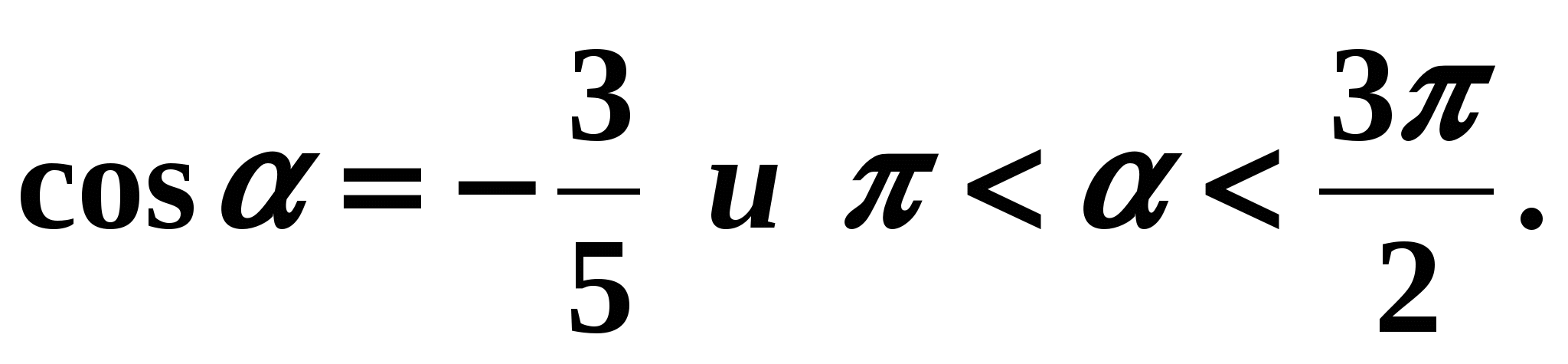 
Określ ćwiartkę, w której znajduje się kąt 
. Kwartał – III. Pamiętajmy, że sinus w trzeciej ćwiartce jest liczbą ujemną, czyli we wzorze (2) przed pierwiastkiem należy postawić znak „-”: Przykład 2.
Oblicz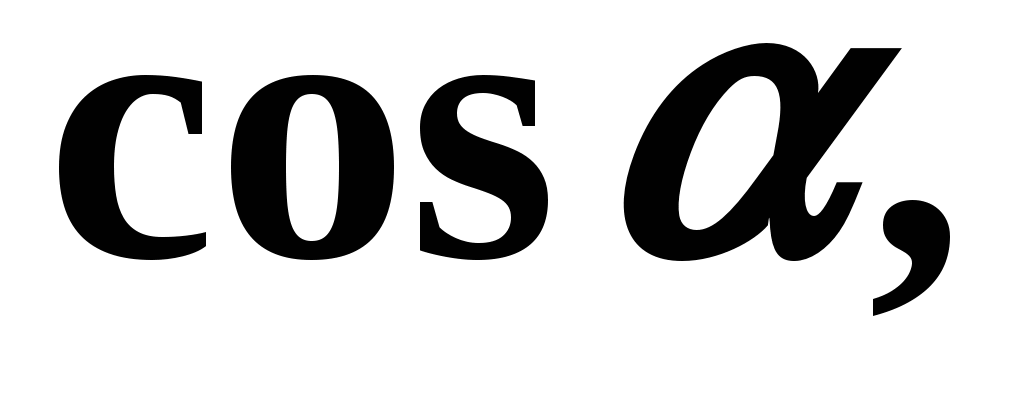 
Jeśli 
Określamy ćwiartkę, w której znajduje się kąt . Kwartał – IV, cosinus w czwartym kwartale jest dodatni. Dlatego we wzorze (3) potrzebny jest znak „+” przed pierwiastkiem: Dowiedzmy się teraz związek między styczną i kotangensem. Z definicji stycznej i cotangensu
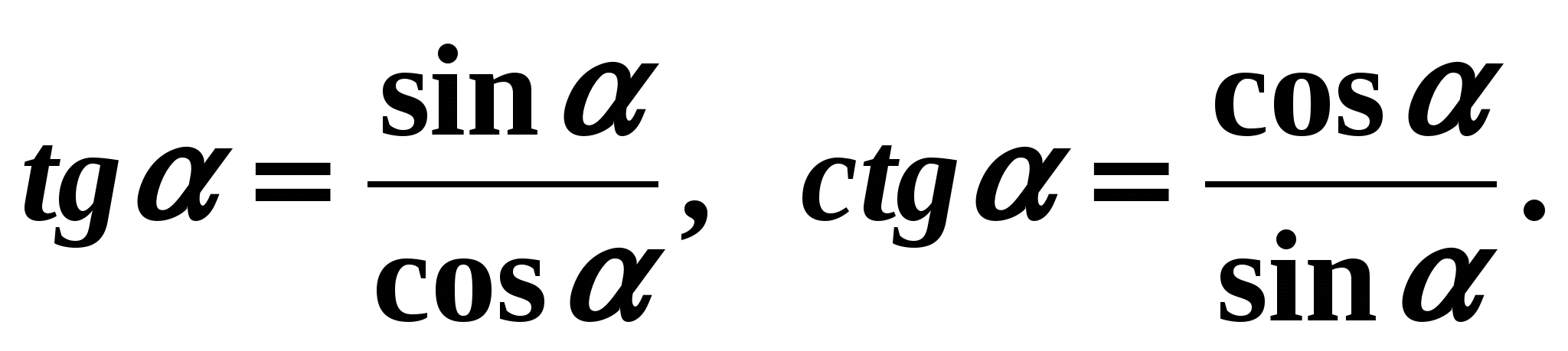
Mnożąc te równości, otrzymujemy:
Z równości (4) możemy wyrazić
Poprzez 
i wzajemnie: 
Równości (4) – (6) są prawdziwe dla wszystkich wartości, dla których
mieć sens, tj. kiedy 
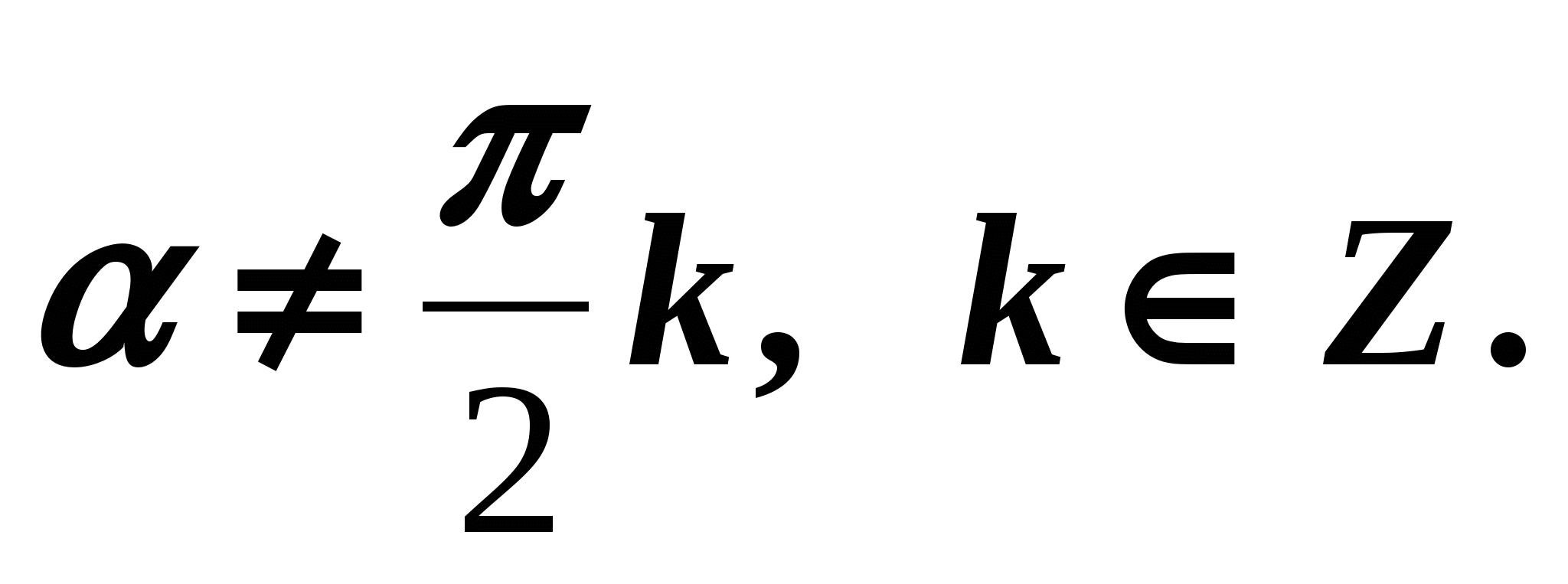Wyprowadźmy teraz wzory wyrażające związek pomiędzy tangensem i cosinusem oraz kotangensem i sinusem tego samego argumentu. Dzielenie obu stron równości (1) przez 
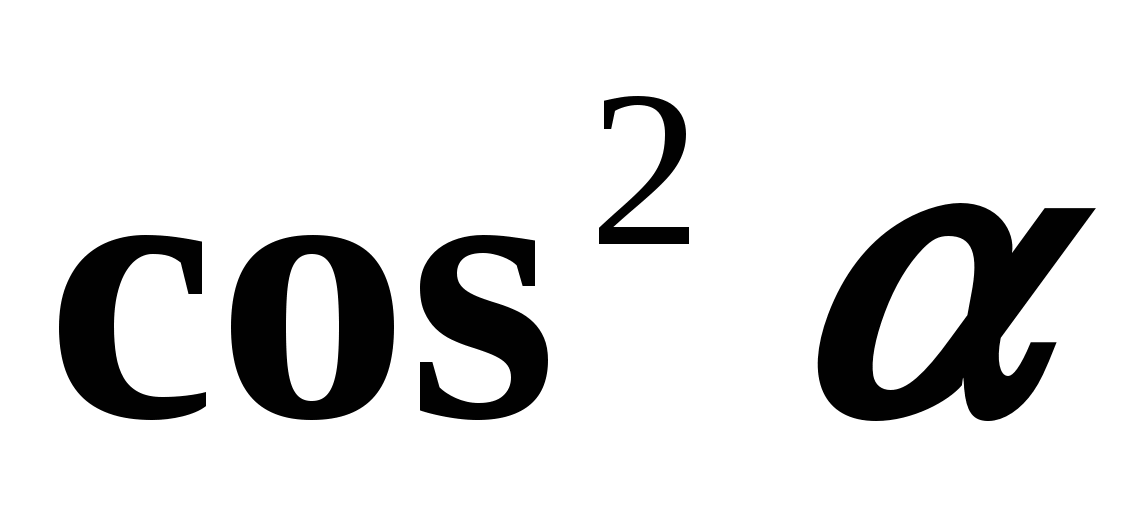, otrzymujemy: 
te.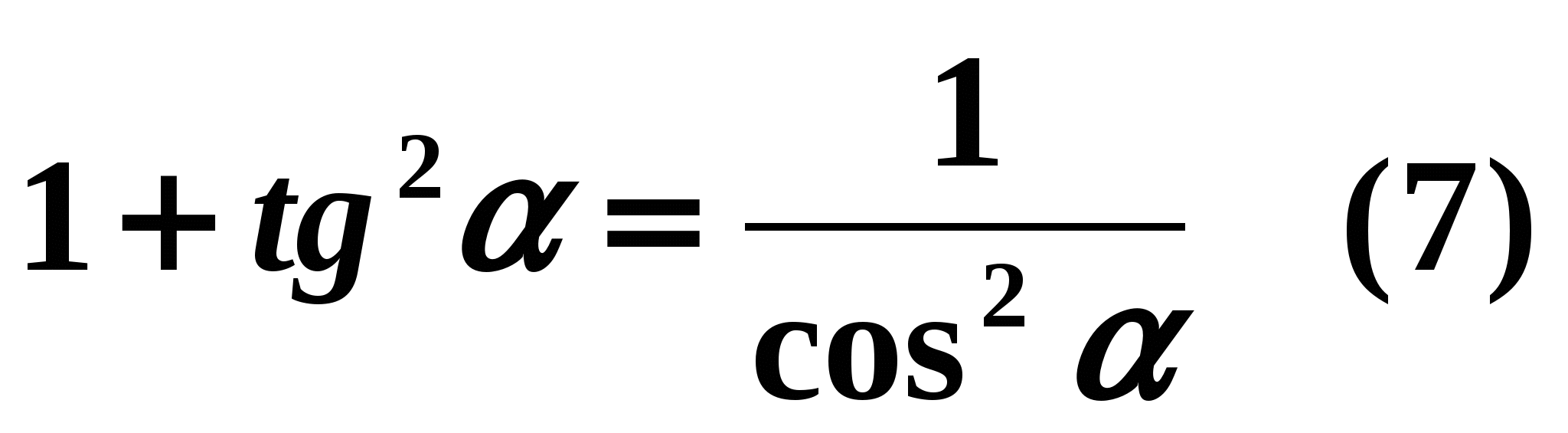 
Jeśli obie strony równości (1) zostaną podzielone przez
, wówczas będziemy mieli: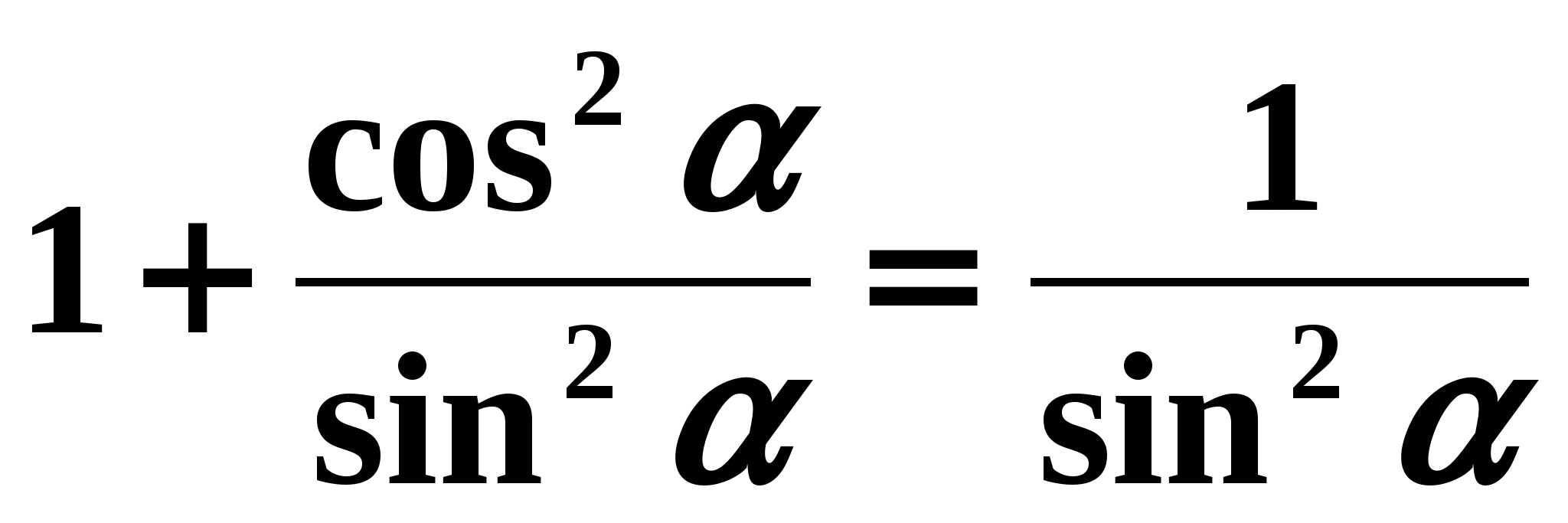 
te.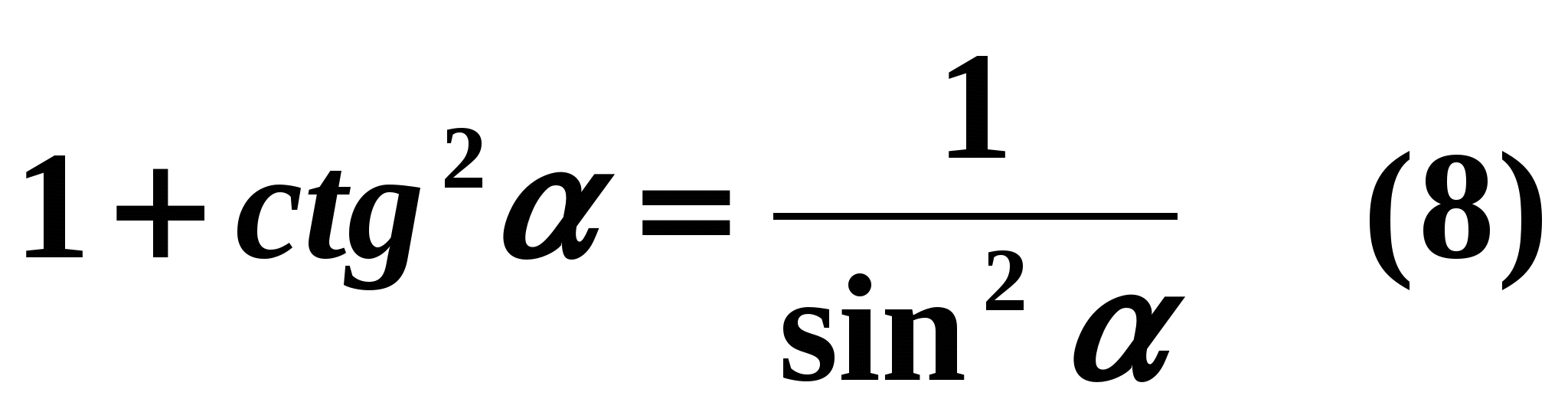 
Przyjrzyjmy się przykładom wykorzystania wyprowadzonych wzorów do znalezienia wartości funkcji trygonometrycznych według znana wartość jeden z nich.
Przykład 1. Dowiedzmy się, czy to wiadomo
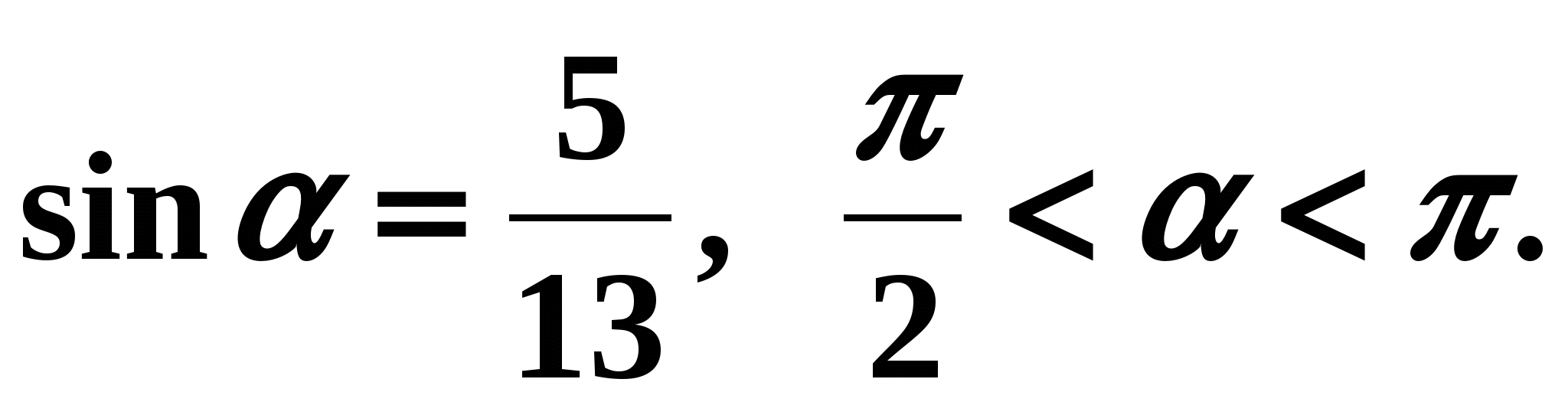Rozwiązanie: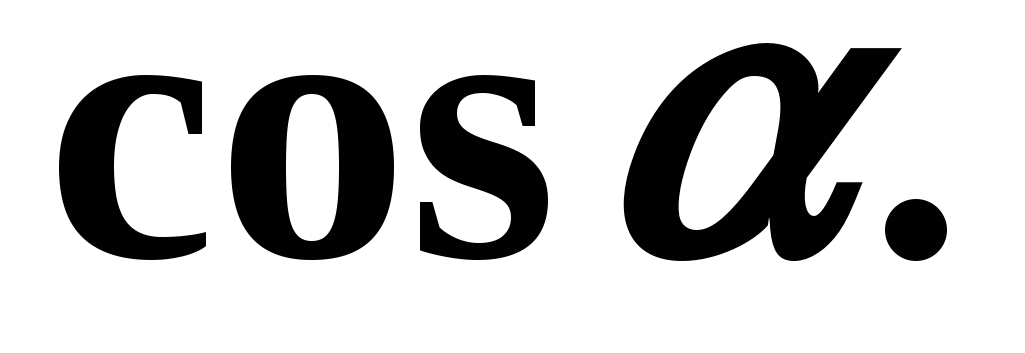 
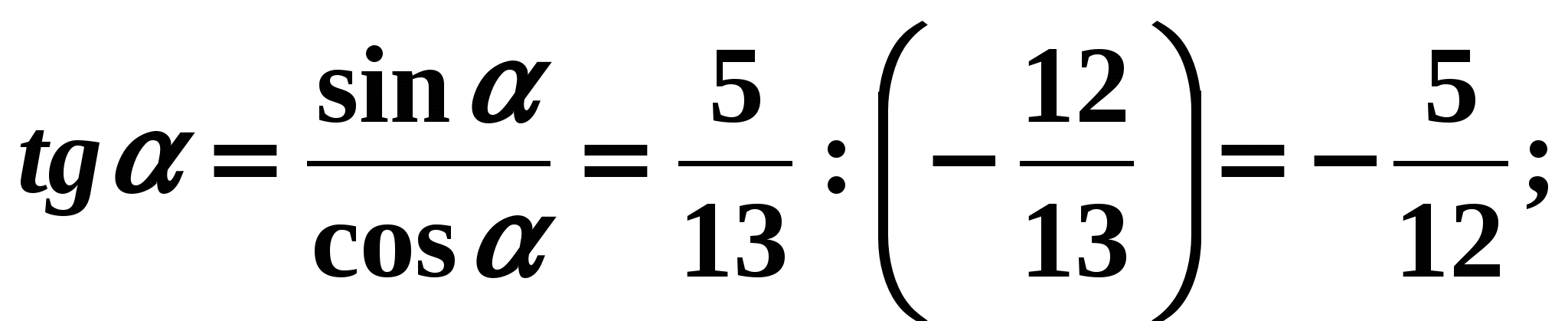
- Aby znaleźć cotangens kąta , wygodnie jest skorzystać ze wzoru (6):
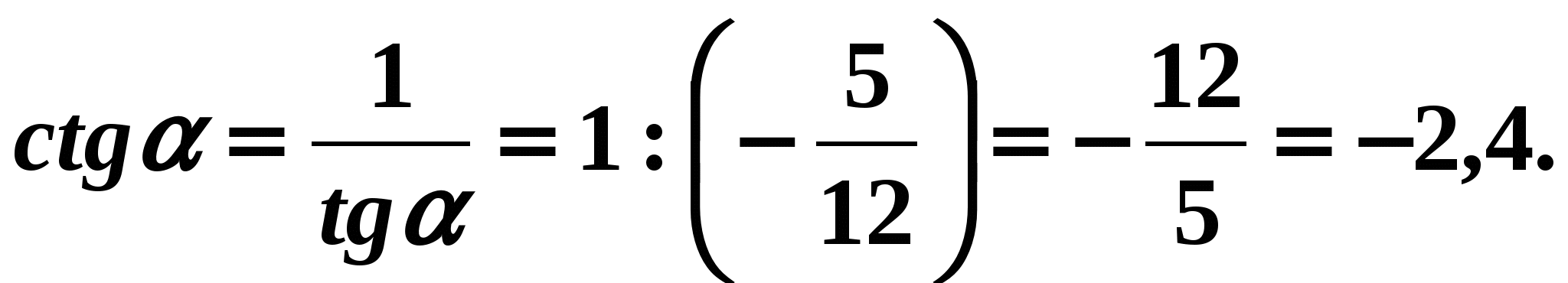Odpowiedź: Przykład 2. Wiadomo, że
. Znajdźmy wszystkie inne funkcje trygonometryczne. Rozwiązanie: - Skorzystajmy ze wzoru (7).
Mamy:
, 
. Zgodnie z warunkami zadania kąt jest kątem 1 ćwiartki, więc jego cosinus jest dodatni. Oznacza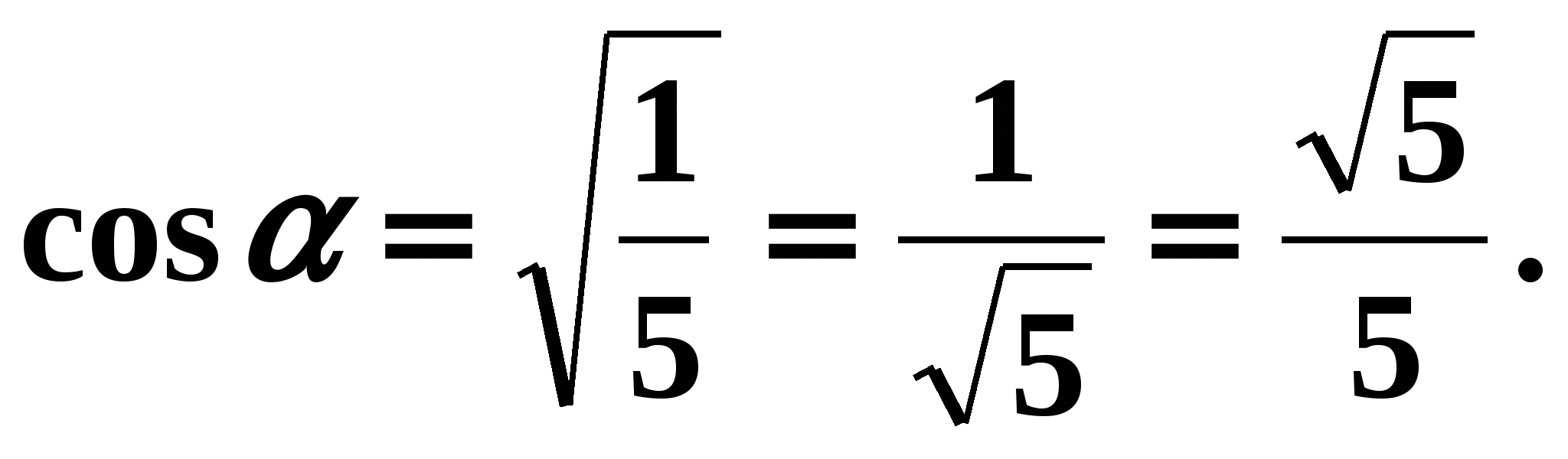 
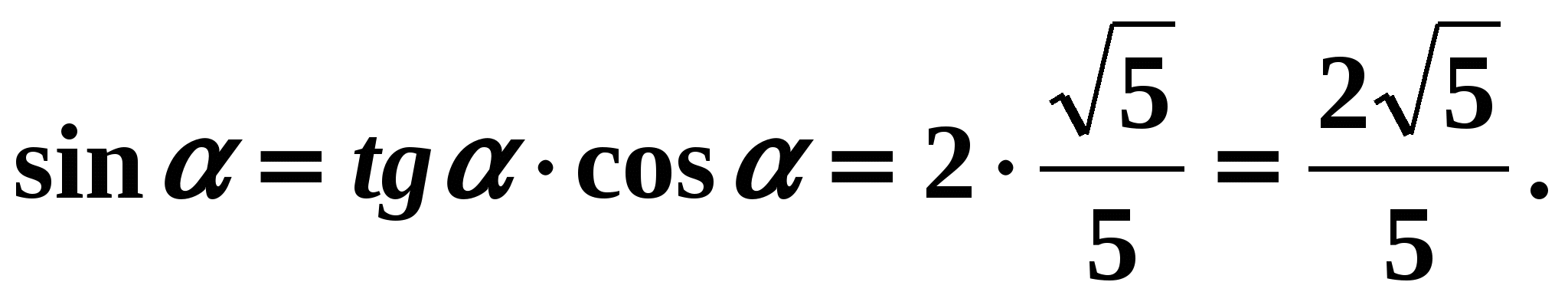
Odpowiedź:
Ustalone zależności pomiędzy funkcjami trygonometrycznymi tego samego argumentu umożliwiają uproszczenie wyrażeń trygonometrycznych. Przykład 3. Uprośćmy wyrażenie:
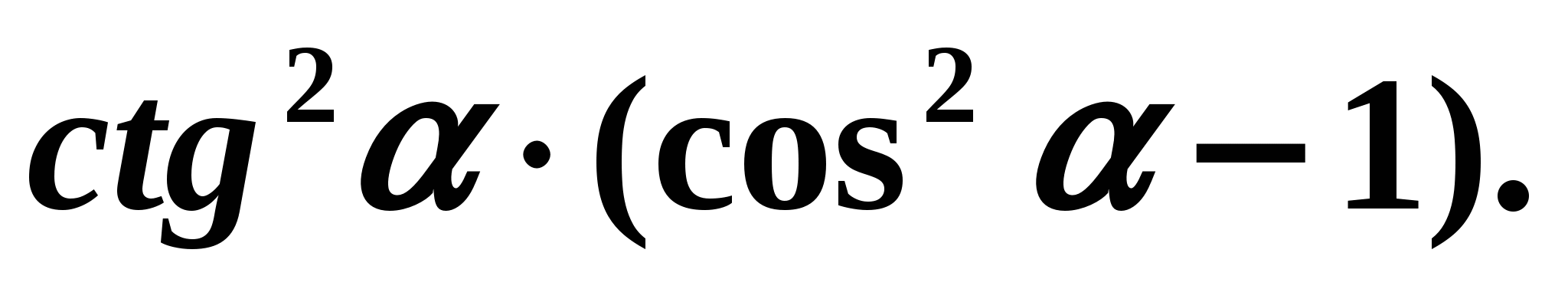Rozwiązanie: Skorzystajmy ze wzorów: 
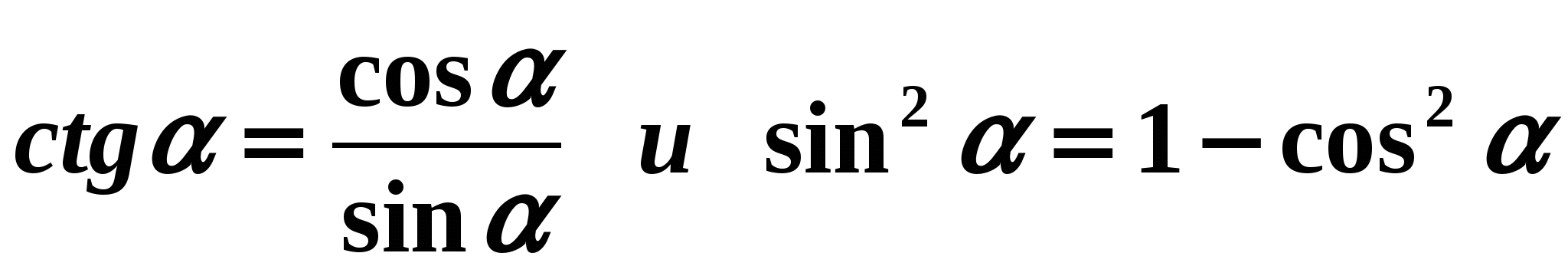. Otrzymujemy: - Konsolidacja.
A teraz na ekranie pojawiają się rubryki samooceny na ten temat. Zaznacz, jaki poziom chciałbyś dzisiaj osiągnąć.
Zrozumiałem temat i potrafię rozwiązać przykłady za pomocą algorytmu, zaglądając do zeszytu, ale z pomocą pytania wiodące(karta - instrukcja).
Rozumiałem temat i potrafię rozwiązywać przykłady korzystając z algorytmu, zaglądając do zeszytu, korzystając ze wskazówek nauczyciela.
Rozumiałem temat i potrafię rozwiązywać przykłady korzystając z algorytmu, patrząc na zeszyt, bez naprowadzających pytań i instrukcji.
Zrozumiałem temat i potrafię rozwiązywać przykłady wykorzystując algorytm bez zaglądania do zeszytu.
Niezależnie od tego, jaki poziom wybierzesz, najpierw dokładnie przejrzyj wszystkie zadania, które ci zleciłem, a następnie wykonaj zadanie odpowiadające wybranemu przez ciebie poziomowi (przed tobą stoją zadania w czterech opcjach, numer opcji odpowiada numerowi opcji) poziom poczucia własnej wartości).
1 opcja
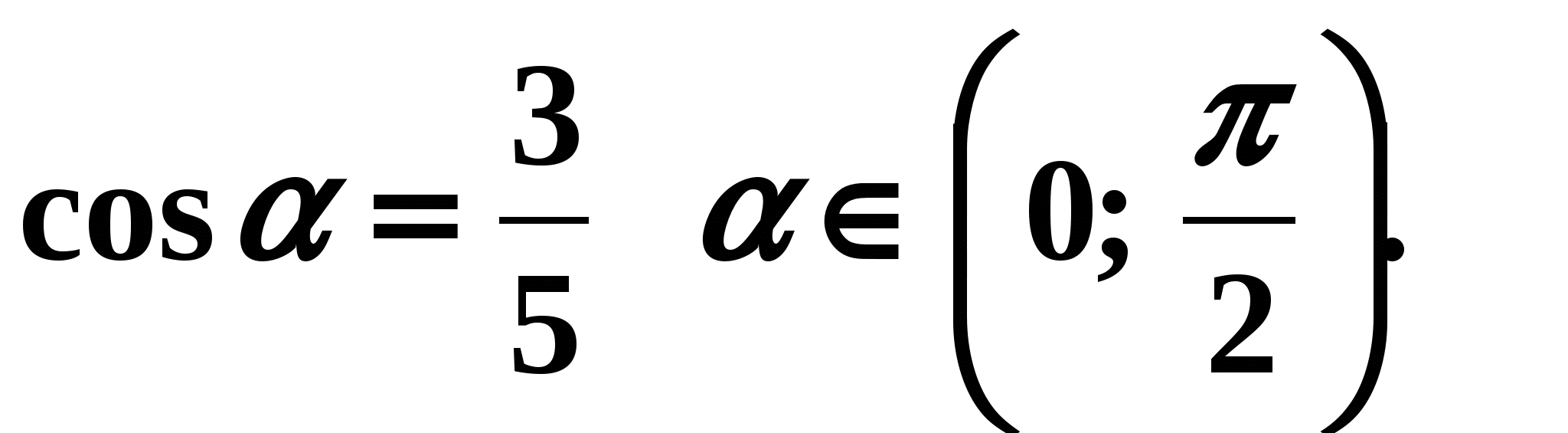Instrukcje:
Opcja 4
A teraz chłopaki, sprawdźmy odpowiedzi. Na ekranie wyświetlane są prawidłowe odpowiedzi, a uczniowie sprawdzają swoją pracę i dopisują punkty do karty lekcji Zadania nr 4. Oceń siebie, korzystając z mapy lekcji. Oblicz swoje punkty i umieść je na karcie.
- Praca domowa.
- Zapisz wszystkie otrzymane wzory w podręczniku. Według podręcznika nr 459 (3, 5), nr 460 (1)
Spróbujmy znaleźć związek między głównymi funkcjami trygonometrycznymi tego samego kąta.
Zależność między cosinusem i sinusem tego samego kąta
Poniższy rysunek przedstawia układ współrzędnych Oxy z przedstawioną w nim częścią półkola jednostkowego ACB ze środkiem w punkcie O. Ta część jest łukiem okręgu jednostkowego. Okrąg jednostkowy opisuje równanie
- x 2 + y 2 =1.
Jak już wiadomo, rzędne y i odcięta x można przedstawić jako sinus i cosinus kąta za pomocą następujących wzorów:
- grzech(a) = y,
- cos(a) = x.
Podstawiając te wartości do równań okręgu jednostkowego otrzymujemy następującą równość
- (sin(a)) 2 + (cos(a)) 2 =1,
Równość ta jest prawdziwa dla dowolnej wartości kąta a. Nazywa się to podstawową tożsamością trygonometryczną.
Z podstawowej tożsamości trygonometrycznej jedną funkcję można wyrazić za pomocą drugiej.
- sin(a) = ±√(1-(cos(a)) 2),
- cos(a) = ±√(1-(sin(a)) 2).
Znak po prawej stronie tego wzoru jest określony przez znak wyrażenia po lewej stronie tego wzoru.
Na przykład.
Oblicz sin(a), jeśli cos(a)=-3/5 i pi Skorzystajmy ze wzoru podanego powyżej: Ponieważ pi Spróbujmy teraz znaleźć związek pomiędzy styczną i kotangensem. Z definicji tg(a) = sin(a)/cos(a), ctg(a) = cos(a)/sin(a). Pomnóżmy te równości i otrzymamy tg(a)*ctg(a) =1. Z tej równości można wyrazić jedną funkcję za pomocą drugiej. Otrzymujemy: Należy rozumieć, że te równości obowiązują tylko wtedy, gdy istnieją tg i ctg, czyli dla dowolnego a, z wyjątkiem a = k*pi/2, dla dowolnej liczby całkowitej k. Spróbujmy teraz, korzystając z podstawowej tożsamości trygonometrycznej, znaleźć związek między tangensem a cosinusem. Podzielmy główną tożsamość trygonometryczną przez (cos(a)) 2. (cos(a) nie jest równe zeru, w przeciwnym razie tangens nie istniałby. Otrzymujemy następującą równość ((sin(a)) 2 + (cos(a)) 2)/ (cos(a)) 2 =1/(cos(a)) 2. Dzieląc wyraz przez wyraz otrzymujemy: Jak zauważono powyżej, wzór ten jest poprawny, jeśli cos(a) nie jest równe zeru, to znaczy dla wszystkich kątów a z wyjątkiem a=pi/2 +pi*k, dla dowolnej liczby całkowitej k. A wykres sinusoidalny jest falą po fali Z studenckiej piosenki. CELE I ZADANIA LEKCJI: OSZCZĘDNOŚĆ ZDROWIA: tworzenie komfortowego klimatu psychologicznego w klasie, atmosfery współpracy uczeń – nauczyciel. WYPOSAŻENIE METODOLOGICZNE LEKCJI: BAZA MATERIAŁOWA I TECHNICZNA: sala matematyczna. WSPARCIE DYDAKTYCZNE LEKCJI: podręcznik, zeszyt, plakaty dotyczące tematu lekcji, tablice, komputer, dyski, ekran, projektor. METODY DZIAŁANIA: praca grupowa i indywidualna przy biurku i tablicy. RODZAJ LEKCJI: lekcja zdobywania nowej wiedzy. PODCZAS ZAJĘĆ 1. Moment organizacyjny: powitanie, sprawdzenie obecności studenta, wypełnienie listy. 2. Sprawdzenie gotowości uczniów do lekcji: wprowadzenie uczniów w nastrój do pracy, przedstawienie im planu lekcji. 3. Analiza błędów w zadaniach domowych. Na ekranie pojawia się obraz poprawnie wykonanej pracy domowej. Każdy uczeń sprawdza ze szczegółowym wyjaśnieniem wstępnym i odnotowuje poprawność wykonania w karcie pracy lekcji. KARTA PRACY LEKCJI. S/o – poczucie własnej wartości. O/t – ocena towarzysza. 4. Aktualizowanie wiedzy, przygotowanie do odbioru nowego materiału. Kolejnym etapem naszej lekcji jest dyktando. Odpowiedzi zapisujemy krótko – mamy rysunek na slajdzie. Dyktowanie (ustne powtórzenie niezbędnych informacji): 1. Zdefiniuj: 2. Zdefiniuj: 3. Zapisz znaki sinusa, cosinusa, tangens, cotangens dla kątów uzyskanych przez obrót punktu P(1;0) o kąt 4. Dla wszystkich tych kątów wskaż ćwiartki płaszczyzny współrzędnych. Dzieci wspólnie z nauczycielem sprawdzają dyktando na slajdzie, wyjaśniając każde stwierdzenie i wystawiając sobie ocenę na karcie lekcji. 5. Z historii trygonometrii. Nowoczesną formę trygonometrii nadał największy matematyk XVIII wieku Leonarda Eulera- Szwajcar z urodzenia, który przez wiele lat pracował w Rosji i był członkiem petersburskiej Akademii Nauk. Wprowadził znane definicje funkcji trygonometrycznych, sformułował i udowodnił wzory redukcyjne, z którymi się jeszcze nie spotkałeś, oraz zidentyfikował klasy funkcji parzystych i nieparzystych. 6. Wprowadzenie nowego materiału: Najważniejsze jest nie tylko poinformowanie studentów o ostatecznych wnioskach, ale uczynienie ich niejako uczestnikami poszukiwań naukowych: poprzez zadawanie pytań w taki sposób, aby rozbudzając swoją ciekawość, zaangażowali się w badania, co pomaga osiągnięcie wyższego poziomu rozwoju umysłowego uczniów. Dlatego wprowadzając nowy materiał stwarzam problematyczną sytuację - jak można łatwiej i bardziej racjonalnie ustalić zależność między sinusem i cosinusem tego samego kąta - poprzez równanie okręgu jednostkowego lub poprzez twierdzenie Pitagorasa. Klasa podzielona jest na opcje na pierwszą i drugą - na ekranie pojawia się slajd z warunkami i rysunkami, nie ma jeszcze rozwiązania. Opcja 1 ustala związek między sinusem i cosinusem poprzez równanie koła o środku w początku i promieniu równym 1x 2 +y 2 =1; grzech 2 + sałata 2 = 1. Opcja 2 ustala związek między sinusem i cosinusem poprzez twierdzenie Pitagorasa - w trójkącie prostokątnym kwadrat przeciwprostokątnej jest równy sumie kwadratów nóg: OB 2 + AB 2 = OA 2 - i otrzymujemy grzech 2 +cos2 =1. Porównują wyniki i wyciągają wnioski: najważniejsze jest to, że równość jest prawdziwa dla dowolnych wartości zawartych w niej liter? Uczniowie muszą odpowiedzieć, że jest to tożsamość (slajd pokazuje prawidłowe rozwiązanie zarówno dla pierwszej, jak i drugiej opcji). Otrzymaliśmy równość obowiązującą dla dowolnych wartości liter w niej zawartych. Jak nazywają się takie równości? Zgadza się – tożsamości. Przypomnijmy, jakie inne tożsamości znamy w algebrze - skrócone wzory na mnożenie: za 2 -b 2 =(a-b)(a+b), (a-b) 2 = a 2 -2ab + b 2, (a+b) 3 =a 3 +3a 2 b+3ab 2 +b 2 , (a-b) 3 =a 3 -3a 2 b+3ab 3 -b 3 , za 3 -b 3 =(a-b)(a 2 +ab+b 2), za 3 +b 3 =(a+b)(a 2 -ab+b 2). Następnym problemem jest to, dlaczego wyprowadziliśmy główną tożsamość trygonometryczną - sin 2 + cos 2 = 1. Zgadza się - znaleźć z jednej znanej wartości sinusa, cosinusa lub tangensa - wartości wszystkich innych funkcji. Teraz ty i ja zawsze możemy używać podstawowej tożsamości trygonometrycznej, ale najważniejsze jest to, że ten sam argument. Zastosowanie zdobytej wiedzy: OPCJA 1 – wyraź sinus poprzez cosinus kąta. Opcja 2 – wyraź cosinus poprzez sinus kąta. Prawidłowa odpowiedź znajduje się na slajdzie Pytanie nauczyciela: czy ktoś zapomniał postawić znaki + i -? Jaki może być kąt? - ktokolwiek. Od czego zależy w tych wzorach znak przed pierwiastkiem? w której ćwiartce znajduje się kąt (argument) definiowanej przez nas funkcji trygonometrycznej. Na tablicy występuje 2 uczniów nr 457. – opcja 1 – 1, opcja 2 – 2. Slajd pokazuje prawidłowe rozwiązanie. Samodzielna praca nad rozpoznaniem podstawowej tożsamości trygonometrycznej 1. znajdź znaczenie wyrażenia: 2. wyrazić liczbę 1 poprzez kąt A, Jeśli Dochodzi do wzajemnego sprawdzenia gotowego slajdu i oceny pracy zarówno poprzez samoocenę, jak i ocenę kolegi. 6. Konsolidacja nowego materiału (wg technologii G.E. Khazankina – technologia zadań pomocniczych). ZADANIE 1. Oblicz ……….. jeśli …………………………………………………………………. 1 uczeń samodzielnie przy tablicy - następnie slajd z właściwym rozwiązaniem. ZADANIE 2. Oblicz……………., jeśli……………………………………………………….. Drugi uczeń przy tablicy, następnie slajd z właściwym rozwiązaniem. 7. Minuta wychowania fizycznego Wiem, że jesteś już dorosły i myślisz, że wcale nie jesteś zmęczony, szczególnie teraz, gdy lekcja trwa tak aktywnie, że czas wydaje się nam wydłużać, zgodnie z teorią A. Einsteina względności, ale zróbmy gimnastykę dla naczyń mózgowych: Znajdźmy teraz związek między styczną i kotangensem............................................................................ ………………… Pojawiło się nowe badanie na ten temat - jaki może być kąt w drugiej tożsamości trygonometrycznej? NAJWAŻNIEJSZE JEST OKREŚLENIE ZBIORU, NA KTÓRYM SPEŁNIAJĄ TE RÓWNOŚCI. ZAZNACZ PUNKTY NA RYSUNKU, W KTÓRYCH NIE ISTNIEJĄ TANGENSY I WSPÓŁCZYNNIKI KĄTA. Trzeci uczeń przy tablicy. Równości obowiązują przez …………………. ZADANIE 3. Oblicz………jeśli………………………. ZADANIE 4. Oblicz…………….. jeśli…………………………………………………………… Pozostali uczniowie pracują w zeszytach. 1 WSPARCIE…………………………………………………………………………………… 2 WSPARCIE…………………………………………………………………………………………………………… 3 WSPARCIE. Zastosowanie podstawowej tożsamości trygonometrycznej do rozwiązywania problemów. 8. Krzyżówka. Anatole France powiedział kiedyś: „Nauka musi być zabawą… Aby strawić wiedzę, musisz ją przyswajać z apetytem”. Aby sprawdzić swoją wiedzę na ten temat, oferujemy Ci krzyżówkę. Po sprawdzeniu krzyżówki dzieci samodzielnie wystawiają oceny na mapie lekcji. Nauczyciel wystawia oceny tym uczniom, którzy byli szczególnie aktywni na lekcji. Wynikiem jest średni wynik za pracę na lekcji. 9. Pouczanie nauczyciela o odrabianiu zadań domowych. 10. Nauczyciel podsumowuje lekcję. 11. Praca domowa: akapit 25 (przed zadaniem 5), nr 459 (parzysty), 460 (parzysty), 463*(4). Podręcznik Sh.A Alimova „Algebra i początki analizy”, 10-11, „Oświecenie”., M., 2005. MAPA LEKCJI „ZALEŻNOŚĆ MIĘDZY SINUSEM, COSINUSEM I STYCZNĄ TEGO SAMEGO KĄTA” Student ________________________________________________________________________________ 1. Znam materiał z poprzednich lekcji Zwrotnica Odpowiedziałem poprawnie na wszystkie pytania, bez notatek. Odpowiedziałem bez notatki z jednym błędem. Odpowiedziałem bez robienia notatek i popełniłem więcej niż jeden błąd. Odpowiedziałem poprawnie na wszystkie pytania, korzystając z notatek. Odpowiedziałem korzystając z notatek, z jednym błędem. Odpowiedziałem, korzystając z notatek, i popełniłem więcej niż jeden błąd 2. Zakończyłem zapisywanie przykładów. Zwrotnica Wszystkie zadania wykonałem bez błędów Zakończyłem z jednym błędem Wykonałem zadania i popełniłem więcej niż dwa błędy 3. Wydedukowałem wzór na znalezienie sinusa i cosinusa Zwrotnica Poprawiłem formuły Wyprowadziłem wzory i popełniłem jeden błąd Wzory wyprowadzałem z pomocą mojego nauczyciela 4. Swoją wiedzę na temat: „Zależność między sinusem, cosinusem i tangensem tego samego kąta” wykorzystałem przy rozwiązywaniu niezależnych prac Zwrotnica Przykłady opcji 1 rozwiązałem bez błędów. Rozwiązałem przykłady opcji 1 i popełniłem błąd. Przykłady opcji 2 rozwiązałem bez błędów. Rozwiązałem przykłady opcji 2 i popełniłem błąd. Rozwiązałem przykłady 3 opcji bez błędów Rozwiązałem przykłady opcji 3 i popełniłem błąd. Rozwiązałem przykłady 4 opcji bez błędów. Rozwiązałem przykłady opcji 4 i popełniłem błąd. 5. Oceń siebie: Rozumiałem wyprowadzenie wzorów i potrafię rozwiązywać przykłady na ten temat za pomocą zeszytu i przy pomocy nauczyciela. Rozumiałem wyprowadzenie wzorów i potrafię samodzielnie rozwiązywać przykłady bez zeszytu, po prostu patrząc na wzory. Rozumiałem wyprowadzanie wzorów i potrafię samodzielnie rozwiązywać przykłady bez zeszytu, a jeśli zapomnę wzoru, sam go wydedukuję. Moje punkty: __________ Maksymalna liczba punktów – 22 18 – 22 punkty - ocena „5” 15 – 17 punktów - ocena „4” 11–14 punktów - wynik „3” Poniżej 11 punktów – należy zgłosić się na konsultację w najbliższych dniach, materiał nie jest jeszcze opanowany. Vera Anatolyevna Golovatova, nauczycielka matematyki GB POU „Okhta College” Podsumowanie dwóch lekcji dla uczniówI
kurs (klasa 10) na temat: „Zależność między sinusem, cosinusem i tangensem tego samego kąta” Cel: zbadaj związek między sinusem, cosinusem i tangensem tego samego kąta. Aby osiągnąć ten cel konieczne jest: Wiedzieć: sformułowania definicji podstawowych funkcji trygonometrycznych (sinus, cosinus i tangens); znaki funkcji trygonometrycznych według ćwiartek; zbiór wartości funkcji trygonometrycznych; podstawowe wzory trygonometrii. Zrozumieć: że podstawowej tożsamości trygonometrycznej można użyć tylko dla tego samego argumentu; algorytm obliczania jednej funkcji trygonometrycznej za pomocą drugiej. Stosować: umiejętność prawidłowego wyboru właściwej formuły do rozwiązania konkretnego zadania; umiejętność pracy z prostymi ułamkami; umiejętność wykonywania przekształceń wyrażeń trygonometrycznych. Analiza: analizować błędy w logice rozumowania. Synteza: zaproponować własny sposób rozwiązywania przykładów; utwórz krzyżówkę wykorzystując zdobytą wiedzę. Stopień: wiedzę i umiejętności na ten temat do wykorzystania w innych działach algebry. Sprzęt:
układ okręgu trygonometrycznego, ulotki ze wzorami i tabelami wartości funkcji trygonometrycznych, komputer, rzutnik multimedialny, prezentacja, arkusze z zadaniami do samodzielnej pracy. Wykorzystane źródła: Algebra i początki analizy: Podręcznik dla klas 10-11. ogólne wykształcenie instytucje / Sh.A.Alimov, Yu.V. Sidorov i wsp. Edukacja, 2006. Zadania Open Bank przygotowujące do egzaminu Unified State Exam z matematyki, 2011. Zasoby sieci INTERNETOWEJ. Krótki plan zajęć: Organizowanie czasu. Pozdrowienia. Przekazywanie celu lekcji i planu lekcji - 3-5 minut Aktualizowanie wiedzy i umiejętności. Uczniowie otrzymują karty lekcji i objaśnienia, jak z nimi pracować. Pytania są wyświetlane na ekranie; uczniowie zapisują odpowiedzi w zeszycie; Nauczyciel wyświetla na ekranie poprawną odpowiedź. Po wypełnieniu ankiety uczniowie dodają punkty do karty lekcji za Zadania nr 1
– 10 minut. Wyjaśnienie nowego materiału. Nauczyciel wyprowadza wzór na podstawową tożsamość trygonometryczną - 5 minut. Uczniowie proszeni są o samodzielne dokończenie nagrania przykładów wyświetlanych na ekranie, sprawdzenie poprawności odpowiedzi oraz dodanie punktów do karty lekcji za Zadania nr 2 –
5 minut. W zeszycie uczniowie proszeni są o samodzielne wyrażenie sinusa przez cosinus i cosinus przez sinus z podstawowej tożsamości trygonometrycznej. Poprawna odpowiedź wyświetlana jest na ekranie, uczniowie sprawdzają i dodają punkty do karty lekcji Zadania nr 3
– 5-7 minut Nauczyciel rozwiązuje przykłady na tablicy wykorzystując podstawową tożsamość trygonometryczną. Podczas objaśnień uczniowie odpowiadają na pytania nauczyciela i zapisują przykłady w zeszytach: 15 minut. Nauczyciel wyprowadza wzory pokazujące zależność stycznej od cotangensu, uczniowie biorą czynny udział w wyprowadzaniu wzorów, odpowiadają na pytania i robią notatki w zeszycie - 5 minut. Nauczyciel wyprowadza wzory pokazujące zależność tangens od cosinus, sinus od cotangens - 5 minut. Uczniowie są dowolnie przywoływani do tablicy i przy pomocy nauczyciela rozwiązują przykłady za pomocą algorytmu. Wszyscy inni zapisują i odpowiadają na pytania, jeśli to konieczne - 10 minut. Utrwalenie poznanego materiału Na koniec lekcji na ekranie wyświetlane są prawidłowe odpowiedzi, uczniowie sprawdzają swoje odpowiedzi i dopisują punkty do karty lekcji Zadania nr 4
– 20 minut. Praca domowa: Uczniowie zapisują zadania domowe w zeszytach – 3 minuty Po wzięciu udziału w seminariach na temat RNS i przeprowadzeniu lekcji przy użyciu mapy technologicznej stało się dla mnie oczywiste, że system ocen stymuluje maksymalne możliwe zainteresowanie uczniów określonym tematem. W moim przypadku są to podstawowe wzory trygonometrii. Studenci często nie dostrzegają trygonometrii, nie tyle ze względu na jej złożoność, ile ze względu na dużą liczbę wzorów, z którymi trzeba umieć pracować. Trudno oczekiwać jakichś niesamowitych sukcesów i wyników po jednej lekcji prowadzonej z wykorzystaniem mapy technologicznej, ale wydaje mi się, że zalety systemu oceniania podczas studiowania trygonometrii i matematyki w ogóle są następujące: możliwe stało się organizowanie i wspomaganie zarówno pracy na lekcjach, jak i samodzielnej, systematycznej pracy uczniów w domu; Powinna wzrosnąć frekwencja i poziom dyscypliny na lekcjach; wzrasta motywacja do działań edukacyjnych; Redukcja stresujących sytuacji związanych z otrzymaniem ocen niezadowalających; Stymulowana jest twórcza postawa wobec pracy. Jedyną wadą RNS (jak mi się wydaje) jest duży nakład pracy nauczyciela, ale to jest praca na rezultaty. Po jednej lekcji prowadzonej przy użyciu tego systemu uczniowie nieustannie pytają, czy będziemy nadal pracować w ten sposób. To znaczy, że byli czymś uzależnieni. Musimy dalej pracować. NIEZALEŻNA PRACA Niezależnie od tego, jaki poziom wybierzesz, najpierw dokładnie przejrzyj wszystkie zadania, które Ci zleciłem, a następnie wykonaj zadanie odpowiadające wybranemu przez Ciebie poziomowi (Zanim otrzymasz zadania czterech opcji, liczba opcji odpowiada poziomom poczucia własnej wartości.) 1 opcja
Instrukcje:
Instrukcje:
Rozwiąż sam ten przykład: Opcja 2
Wskazówka: Aby wyznaczyć funkcję cosinus, skorzystaj ze wzoru (3) z dzisiejszej lekcji. Nie zapomnij określić znaku, który pojawi się przed korzeniem. Aby obliczyć wartości tangensa i cotangensu, możesz skorzystać z definicji tych funkcji lub skorzystać ze wzorów, które opracowaliśmy dzisiaj na zajęciach. Notatka. Pogrupuj pierwszy i trzeci wyraz wyrażenia, usuń wspólny czynnik z nawiasów.... Opcja 3
Opcja 4
Powtórzenie: 1. W której ćwiartce znajduje się kąt 1 radian i ile to jest w przybliżeniu równe? W pierwszym kwartale 1 rad. 57,3° 2. Jakiego słowa brakuje w definicji funkcji sinus? Sinus kąta
zwane ………… punktami okręgu jednostkowego. RZĘDNA 3. Jakiego słowa brakuje w definicji funkcji cosinus? Cosinus kąta
zwany …………
punkty okręgu jednostkowego. ODCIĘTA 4. Uzupełnij formułę:
tg
5. Określ znak produktu: tg
6. Jaką wartość może przyjmować sinus?
Lub
7. Oblicz: y
B(x;y)
R
T=grzech
O
X
x=cos
Dokończ nagranie:
X
y
X
y
X
X
X
y
X
y
X
X
Opcja 1: Opcja 3: Opcja 2: Opcja 4:Zależność między styczną i cotangensem tego samego kąta
Oś x ucieka.
„Krótki plan”Wyświetl zawartość dokumentu
"Odbicie"Wyświetl zawartość dokumentu
"Niezależna praca"
Wyświetl zawartość prezentacji
"Prezentacja"
