$X$. Para empezar, recordemos la siguiente definición:
Definición 1
Población-- un conjunto de objetos de un tipo determinado seleccionados aleatoriamente, sobre los cuales se realizan observaciones para obtener valores específicos variable aleatoria llevado a cabo en condiciones constantes al estudiar una variable aleatoria de un tipo determinado.
Definición 2
variación general-- promedio aritmética de cuadrados desviaciones de los valores de una variante poblacional de su valor promedio.
Sean los valores de la opción $x_1,\ x_2,\dots ,x_k$ que tengan, respectivamente, frecuencias $n_1,\ n_2,\dots ,n_k$. Entonces variación general calculado por la fórmula:
Consideremos un caso especial. Deje que todas las opciones $x_1,\ x_2,\dots,x_k$ sean diferentes. En este caso $n_1,\ n_2,\dots,n_k=1$. Encontramos que en este caso la varianza general se calcula mediante la fórmula:
Este concepto también está asociado con el concepto de desviación estándar general.
Definición 3
Promedio general Desviación Estándar
\[(\sigma )_g=\sqrt(D_g)\]
varianza muestral
Se nos dará una población muestral con respecto a una variable aleatoria $X$. Para empezar, recordemos la siguiente definición:
Definición 4
Población de muestra -- parte de objetos seleccionados de la población general.
Definición 5
varianza muestral-- promedio valores aritméticos opción de muestreo.
Sean los valores de la opción $x_1,\ x_2,\dots ,x_k$ que tengan, respectivamente, frecuencias $n_1,\ n_2,\dots ,n_k$. Luego, la varianza muestral se calcula mediante la fórmula:
Consideremos un caso especial. Deje que todas las opciones $x_1,\ x_2,\dots,x_k$ sean diferentes. En este caso $n_1,\ n_2,\dots,n_k=1$. Encontramos que en este caso la varianza muestral se calcula mediante la fórmula:
También relacionado con este concepto está el concepto de desviación estándar muestral.
Definición 6
Desviación estándar muestral -- Raíz cuadrada de la variación general:
\[(\sigma )_в=\sqrt(D_в)\]
Varianza corregida
Para encontrar la varianza corregida $S^2$ es necesario multiplicar la varianza muestral por la fracción $\frac(n)(n-1)$, es decir
Este concepto también está asociado con el concepto de desviación estándar corregida, que se obtiene mediante la fórmula:
En el caso de que los valores de las variantes no sean discretos, sino que representen intervalos, en las fórmulas para calcular las varianzas generales o muestrales, el valor de $x_i$ se toma como el valor de la mitad del intervalo a cual pertenece $x_i.$.
Un ejemplo de un problema para encontrar la varianza y la desviación estándar.
Ejemplo 1
La población de muestra está definida por la siguiente tabla de distribución:
Foto 1.
Encontremos la varianza muestral, la desviación estándar muestral, la varianza corregida y la desviación estándar corregida.
Para solucionar este problema, primero hacemos una tabla de cálculo:
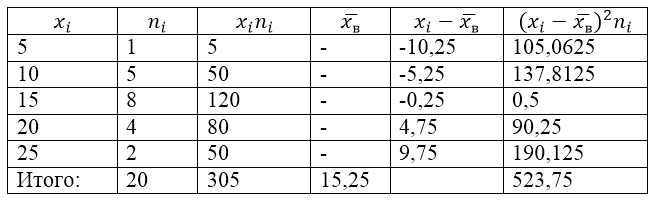
Figura 2.
El valor $\overline(x_в)$ (promedio de la muestra) en la tabla se encuentra mediante la fórmula:
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15.25\]
Encontremos la varianza muestral usando la fórmula:
Desviación estándar de la muestra:
\[(\sigma )_в=\sqrt(D_в)\aprox 5.12\]
Varianza corregida:
\[(S^2=\frac(n)(n-1)D)_в=\frac(20)(19)\cdot 26.1875\aprox 27.57\]
Desviación estándar corregida.
El programa Excel es muy valorado tanto por profesionales como por aficionados, porque usuarios de cualquier nivel pueden trabajar con él. Por ejemplo, cualquier persona con habilidades mínimas de “comunicación” en Excel puede dibujar un gráfico simple, hacer un plato decente, etc.
Al mismo tiempo, este programa incluso le permite realizar varios tipos de cálculos, por ejemplo, cálculos, pero esto requiere un nivel de formación ligeramente diferente. Sin embargo, si acaba de empezar a familiarizarse con este programa y está interesado en todo lo que le ayudará a convertirse en un usuario más avanzado, este artículo es para usted. Hoy te diré qué es la fórmula de la desviación estándar en Excel, por qué es necesaria y, estrictamente hablando, cuándo se usa. ¡Ir!
Lo que es
Empecemos con la teoría. La desviación estándar suele denominarse raíz cuadrada que se obtiene de la media aritmética de todas las diferencias al cuadrado entre las cantidades disponibles, así como de su media aritmética. Por cierto, este valor se suele llamar la letra griega "sigma". La desviación estándar se calcula mediante la fórmula STANDARDEVAL; en consecuencia, el programa lo hace por sí mismo.
La esencia de este concepto es identificar el grado de variabilidad de un instrumento, es decir, es, a su manera, un indicador derivado de la estadística descriptiva. Identifica cambios en la volatilidad de un instrumento durante un período de tiempo determinado. Usando las fórmulas de desviación estándar, puedes estimar Desviación Estándar al recuperar, se ignoran los valores lógicos y de texto.
Fórmula
Ayuda a calcular la desviación estándar en fórmula de excel, que se proporciona automáticamente en programa excel. Para encontrarlo, debes buscar la sección de fórmulas en Excel y luego seleccionar la que se llama ESTANDARDEVAL, por lo que es muy simple.
Después de eso, aparecerá una ventana frente a usted en la que deberá ingresar datos para el cálculo. En particular, se deben ingresar dos números en campos especiales, después de lo cual el programa calculará la desviación estándar de la muestra.

Sin duda, las fórmulas y los cálculos matemáticos son una cuestión bastante compleja y no todos los usuarios pueden afrontarla de inmediato. Sin embargo, si profundizas un poco más y miras el tema con un poco más de detalle, resulta que no todo es tan triste. Espero que esté convencido de esto con el ejemplo del cálculo de la desviación estándar.
Vídeo para ayudar
A sabios matemáticos y estadísticos se les ocurrió un indicador más confiable, aunque con un propósito ligeramente diferente: promedio desviación lineal . Este indicador caracteriza la medida de dispersión de los valores de un conjunto de datos en torno a su valor medio.
Para mostrar la medida de la dispersión de los datos, primero debe decidir con qué se calculará esta dispersión; normalmente este es el valor promedio. A continuación, debe calcular qué tan lejos están los valores del conjunto de datos analizado del promedio. Está claro que a cada valor le corresponde un determinado valor de desviación, pero nos interesa la valoración global, que abarque a toda la población. Por lo tanto, la desviación promedio se calcula utilizando la fórmula habitual de media aritmética. ¡Pero! Pero para calcular el promedio de las desviaciones, primero hay que sumarlas. Y si sumamos números positivos y negativos, se anularán entre sí y su suma tenderá a cero. Para evitar esto, todas las desviaciones se toman en módulo, es decir, todos los números negativos se vuelven positivos. Ahora la desviación media mostrará una medida generalizada de la dispersión de valores. Como resultado, la desviación lineal promedio se calculará mediante la fórmula:
a– desviación lineal media,
X– el indicador analizado, con un guión arriba – el valor medio del indicador,
norte– número de valores en el conjunto de datos analizados,
Espero que el operador de suma no asuste a nadie.
La desviación lineal promedio calculada utilizando la fórmula especificada refleja la desviación absoluta promedio del valor promedio para una población determinada.

En la imagen, la línea roja es el valor medio. Las desviaciones de cada observación de la media se indican con flechas pequeñas. Se toman módulo y se resumen. Luego todo se divide por el número de valores.
Para completar el cuadro, necesitamos dar un ejemplo. Digamos que hay una empresa que produce esquejes para palas. Cada corte debe tener una longitud de 1,5 metros, pero lo más importante es que todos sean iguales o al menos más o menos 5 cm, pero los trabajadores descuidados cortarán 1,2 mo 1,8 m. Los veraneantes están descontentos. El director de la empresa decidió realizar un análisis estadístico de la longitud de los esquejes. Seleccioné 10 piezas y medí su longitud, encontré el promedio y calculé la desviación lineal promedio. El promedio resultó ser exactamente lo que se necesitaba: 1,5 m. Pero la desviación lineal promedio fue de 0,16 m. Por lo tanto, resulta que cada corte es en promedio 16 cm más largo o más corto que lo necesario. Hay algo de qué hablar con el trabajadores. De hecho, no he visto ningún uso real de este indicador, así que se me ocurrió un ejemplo. Sin embargo, existe tal indicador en las estadísticas.
Dispersión
Al igual que la desviación lineal promedio, la varianza también refleja el grado de dispersión de los datos alrededor del valor medio.
La fórmula para calcular la varianza se ve así:
 (para series de variación (varianza ponderada))
(para series de variación (varianza ponderada))
 (para datos no agrupados (varianza simple))
(para datos no agrupados (varianza simple))
Donde: σ 2 – dispersión, Xi– analizamos el indicador sq (el valor de la característica), – el valor promedio del indicador, f i – el número de valores en el conjunto de datos analizados.
La dispersión es el cuadrado promedio de las desviaciones.
Primero, se calcula el valor promedio, luego se toma la diferencia entre cada valor original y promedio, se eleva al cuadrado, se multiplica por la frecuencia del valor del atributo correspondiente, se suma y luego se divide por el número de valores en la población.
Sin embargo, en forma pura, como la media aritmética o índice, no se utiliza la varianza. Es más bien un indicador auxiliar e intermedio que se utiliza para otros tipos de análisis estadístico.
Una forma simplificada de calcular la varianza
![]()
Desviación Estándar
Para utilizar la varianza para el análisis de datos, se toma la raíz cuadrada de la varianza. Resulta el llamado Desviación Estándar.

Por cierto, la desviación estándar también se llama sigma, de la letra griega que la denota.
La desviación estándar, obviamente, también caracteriza la medida de la dispersión de los datos, pero ahora (a diferencia de la varianza) se puede comparar con los datos originales. Como regla general, las medidas cuadráticas medias en estadística dan resultados más precisos que las lineales. Por lo tanto, la desviación estándar es una medida más precisa de la dispersión de los datos que la desviación media lineal.
Desviación Estándar(sinónimos: Desviación Estándar, Desviación Estándar, desviación cuadrada; términos relacionados: Desviación Estándar, extensión estándar) - en teoría de la probabilidad y estadística, el indicador más común de la dispersión de los valores de una variable aleatoria en relación con su expectativa matemática. Con conjuntos limitados de muestras de valores, en lugar de la expectativa matemática, se utiliza la media aritmética del conjunto de muestras.
YouTube enciclopédico
-
1 / 5
La desviación estándar se mide en unidades de medida de la propia variable aleatoria y se utiliza al calcular el error estándar de la media aritmética, al construir intervalos de confianza, al probar estadísticamente hipótesis, al medir la relación lineal entre variables aleatorias. Definida como la raíz cuadrada de la varianza de una variable aleatoria.
Desviación Estándar:
s = norte norte − 1 σ 2 = 1 norte − 1 ∑ yo = 1 norte (x yo − x ¯) 2 ; (\displaystyle s=(\sqrt ((\frac (n)(n-1))\sigma ^(2)))=(\sqrt ((\frac (1)(n-1))\sum _( i=1)^(n)\left(x_(i)-(\bar (x))\right)^(2)));)- Nota: Muy a menudo hay discrepancias en los nombres de MSD (desviación cuadrática media) y STD (desviación estándar) con sus fórmulas. Por ejemplo, en el módulo numPy del lenguaje de programación Python, la función std() se describe como "desviación estándar", mientras que la fórmula refleja la desviación estándar (división por la raíz de la muestra). En Excel, la función ESTANDARDEVAL() es diferente (división por la raíz de n-1).
Desviación Estándar(estimación de la desviación estándar de una variable aleatoria X en relación con su expectativa matemática basada en una estimación insesgada de su varianza) s (\displaystyle s):
σ = 1 norte ∑ yo = 1 norte (x yo − x ¯) 2 . (\displaystyle \sigma =(\sqrt ((\frac (1)(n))\sum _(i=1)^(n)\left(x_(i)-(\bar (x))\right) ^(2))).)Dónde σ 2 (\displaystyle \sigma ^(2))- dispersión; x yo (\displaystyle x_(i)) - iº elemento de la selección; norte (\ Displaystyle n)- tamaño de la muestra; - media aritmética de la muestra:
x ¯ = 1 norte ∑ yo = 1 norte x yo = 1 norte (x 1 + … + x norte) . (\displaystyle (\bar (x))=(\frac (1)(n))\sum _(i=1)^(n)x_(i)=(\frac (1)(n))(x_ (1)+\ldots +x_(n)).)Cabe señalar que ambas estimaciones están sesgadas. En el caso general, es imposible elaborar una estimación insesgada. Sin embargo, la estimación basada en la estimación de la varianza insesgada es consistente.
De acuerdo con GOST R 8.736-2011, la desviación estándar se calcula utilizando la segunda fórmula de esta sección. Por favor verifique los resultados.
regla tres sigma
regla tres sigma (3 σ (\displaystyle 3\sigma)) - casi todos los valores de una variable aleatoria distribuida normalmente se encuentran en el intervalo (x ¯ − 3 σ ; x ¯ + 3 σ) (\displaystyle \left((\bar (x))-3\sigma ;(\bar (x))+3\sigma \right)). Más estrictamente, con una probabilidad de aproximadamente 0,9973, el valor de una variable aleatoria distribuida normalmente se encuentra en el intervalo especificado (siempre que el valor x ¯ (\displaystyle (\bar (x))) verdadero y no obtenido como resultado del procesamiento de la muestra).
Si el valor verdadero x ¯ (\displaystyle (\bar (x))) es desconocido, entonces no deberías usar σ (\displaystyle \sigma), A s. Así, la regla de tres sigma se transforma en regla de tres. s .
Interpretación del valor de la desviación estándar.
Un valor de desviación estándar mayor muestra una mayor dispersión de valores en el conjunto presentado con el valor promedio del conjunto; Por lo tanto, un valor más pequeño muestra que los valores del conjunto están agrupados alrededor del valor promedio.
Por ejemplo, tenemos tres conjuntos numéricos: (0, 0, 14, 14), (0, 6, 8, 14) y (6, 6, 8, 8). Los tres conjuntos tienen valores medios iguales a 7 y desviaciones estándar, respectivamente, iguales a 7, 5 y 1. El último conjunto tiene una desviación estándar pequeña, ya que los valores del conjunto se agrupan alrededor del valor medio; el primer conjunto tiene más gran importancia desviación estándar: los valores dentro del conjunto difieren mucho del valor promedio.
En sentido general, la desviación estándar puede considerarse una medida de incertidumbre. Por ejemplo, en física, la desviación estándar se utiliza para determinar el error de una serie de mediciones sucesivas de alguna cantidad. Este valor es muy importante para determinar la plausibilidad del fenómeno en estudio en comparación con el valor predicho por la teoría: si el valor promedio de las mediciones difiere mucho de los valores predichos por la teoría (gran desviación estándar), luego se deben volver a verificar los valores obtenidos o el método para obtenerlos. identificados con riesgo de cartera.
Clima
Supongamos que hay dos ciudades con la misma temperatura máxima diaria promedio, pero una está ubicada en la costa y la otra en la llanura. Se sabe que las ciudades ubicadas en la costa tienen muchas temperaturas máximas diurnas diferentes que son más bajas que las ciudades ubicadas en el interior. Por lo tanto, la desviación estándar de las temperaturas máximas diarias para una ciudad costera será menor que para la segunda ciudad, a pesar de que el valor promedio de este valor es el mismo, lo que en la práctica significa que la probabilidad de que la temperatura máxima del aire en cualquier día del año será mayor que el valor medio, mayor para una ciudad situada en el interior.
Deporte
Supongamos que hay varios equipos de fútbol que se clasifican según algún conjunto de parámetros, por ejemplo, el número de goles marcados y concedidos, oportunidades de gol, etc. Lo más probable es que el mejor equipo de este grupo tenga mejores valores. en más parámetros. Cuanto menor sea la desviación estándar del equipo para cada uno de los parámetros presentados, más predecible será el resultado del equipo; dichos equipos están equilibrados. Por otro lado, el equipo con gran valor La desviación estándar dificulta predecir el resultado, lo que a su vez se explica por un desequilibrio, por ejemplo, una defensa fuerte pero un ataque débil.
El uso de la desviación estándar de los parámetros del equipo permite, en un grado u otro, predecir el resultado de un partido entre dos equipos, evaluando las fortalezas y lados débilesórdenes y, por tanto, los métodos de lucha elegidos.
Vale la pena señalar que este cálculo de la varianza tiene un inconveniente: resulta sesgado, es decir, su valor esperado no es igual al valor real de la varianza. Lea más sobre esto. Al mismo tiempo, no todo es tan malo. A medida que aumenta el tamaño de la muestra, todavía se acerca a su análogo teórico, es decir. es asintóticamente insesgado. Por lo tanto, cuando se trabaja con tallas grandes muestras, puede utilizar la fórmula anterior.
Es útil traducir el lenguaje de signos al lenguaje de palabras. Resulta que la varianza es el cuadrado promedio de las desviaciones. Es decir, primero se calcula el valor promedio, luego se toma la diferencia entre cada valor original y promedio, se eleva al cuadrado, se suma y luego se divide por el número de valores de la población. La diferencia entre un valor individual y el promedio refleja la medida de la desviación. Se eleva al cuadrado para que todas las desviaciones se conviertan en números exclusivamente positivos y para evitar la destrucción mutua de las desviaciones positivas y negativas al sumarlas. Luego, dadas las desviaciones al cuadrado, simplemente calculamos la media aritmética. Promedio - cuadrado - desviaciones. Las desviaciones se elevan al cuadrado y se calcula el promedio. La solución está en sólo tres palabras.
Sin embargo, en su forma pura, como la media aritmética o índice, no se utiliza la dispersión. Es más bien un indicador auxiliar e intermedio necesario para otros tipos de análisis estadístico. Ni siquiera tiene una unidad de medida normal. A juzgar por la fórmula, este es el cuadrado de la unidad de medida de los datos originales. Sin botella, como dicen, no puedes entenderlo.
(módulo 111)
Para devolver la varianza a la realidad, es decir, utilizarla para fines más mundanos, se extrae de ella la raíz cuadrada. Resulta el llamado desviación estándar (RMS). Hay nombres de "desviación estándar" o "sigma" (del nombre de la letra griega). La fórmula de la desviación estándar es:

Para obtener este indicador para la muestra, utilice la fórmula:

Al igual que con la varianza, existe una opción de cálculo ligeramente diferente. Pero a medida que la muestra crece, la diferencia desaparece.
La desviación estándar, obviamente, también caracteriza la medida de dispersión de datos, pero ahora (a diferencia de la dispersión) se puede comparar con los datos originales, ya que tienen las mismas unidades de medida (esto se desprende de la fórmula de cálculo). Pero este indicador en su forma pura no es muy informativo, ya que contiene demasiados cálculos intermedios que resultan confusos (desviación, cuadrado, suma, promedio, raíz). Sin embargo, ya es posible trabajar directamente con la desviación estándar, porque las propiedades de este indicador están bien estudiadas y conocidas. Por ejemplo, existe este regla tres sigma, que establece que los datos tienen 997 valores de 1000 dentro de ±3 sigma de la media aritmética. La desviación estándar, como medida de incertidumbre, también interviene en muchos cálculos estadísticos. Con su ayuda, se determina el grado de precisión de diversas estimaciones y pronósticos. Si la variación es muy grande, entonces la desviación estándar también será grande y, por tanto, el pronóstico será inexacto, lo que se expresará, por ejemplo, en intervalos de confianza muy amplios.
El coeficiente de variación.
La desviación estándar da una estimación absoluta de la medida de dispersión. Por lo tanto, para comprender qué tan grande es el diferencial en relación con los valores mismos (es decir, independientemente de su escala), se requiere un indicador relativo. Este indicador se llama coeficiente de variación y se calcula mediante la siguiente fórmula:
El coeficiente de variación se mide como porcentaje (si se multiplica por 100%). Con este indicador, puede comparar una variedad de fenómenos, independientemente de su escala y unidades de medida. Este hecho y hace que el coeficiente de variación sea tan popular.
En estadística se acepta que si el valor del coeficiente de variación es menor al 33%, entonces la población se considera homogénea; si es mayor al 33%, entonces es heterogénea. Es difícil para mí comentar algo aquí. No sé quién definió esto y por qué, pero se considera un axioma.
Siento que me dejo llevar por la teoría seca y necesito aportar algo visual y figurativo. Por otro lado, todos los indicadores de variación describen aproximadamente lo mismo, sólo que se calculan de forma diferente. Por lo tanto, es difícil mostrar una variedad de ejemplos: sólo pueden diferir los valores de los indicadores, pero no su esencia. Entonces, comparemos cómo difieren los valores de varios indicadores de variación para el mismo conjunto de datos. Tomemos el ejemplo del cálculo de la desviación lineal promedio (de ). Aquí están los datos de origen:

Y un horario para recordártelo.

Con estos datos calculamos varios indicadores variaciones.
El valor medio es la media aritmética habitual.
El rango de variación es la diferencia entre el máximo y el mínimo:
La desviación lineal promedio se calcula mediante la fórmula:
Desviación Estándar:
Resumamos el cálculo en una tabla.

Como puede verse, la media lineal y la desviación estándar dan valores similares para el grado de variación de los datos. La varianza es sigma al cuadrado, por lo que siempre será relativa un número grande, lo cual, de hecho, no significa nada. El rango de variación es la diferencia entre valores extremos y puede decir mucho.
Resumamos algunos resultados.
La variación de un indicador refleja la variabilidad de un proceso o fenómeno. Su grado se puede medir utilizando varios indicadores.
1. Rango de variación: la diferencia entre el máximo y el mínimo. Refleja el rango valores posibles.
2. Desviación lineal promedio: refleja el promedio de las desviaciones absolutas (módulo) de todos los valores de la población analizada de su valor promedio.
3. Dispersión: el cuadrado medio de las desviaciones.
4. La desviación estándar es la raíz de la dispersión (el cuadrado medio de las desviaciones).
5. El coeficiente de variación es el indicador más universal y refleja el grado de dispersión de los valores, independientemente de su escala y unidades de medida. El coeficiente de variación se mide como porcentaje y se puede utilizar para comparar la variación de diferentes procesos y fenómenos.Así, en análisis estadístico existe un sistema de indicadores que reflejan la homogeneidad de los fenómenos y la estabilidad de los procesos. A menudo, los indicadores de variación no tienen un significado independiente y se utilizan para análisis de datos adicionales (cálculo de intervalos de confianza).


