Probability theory is a special branch of mathematics that is studied only by students of higher educational institutions. Do you like calculations and formulas? You are not afraid of the prospects of getting acquainted with the normal distribution, ensemble entropy, mathematical expectation and discrete dispersion random variable? Then this subject will be very interesting to you. Let's get acquainted with several of the most important basic concepts of this branch of science.
Let's remember the basics
Even if you remember the most simple concepts theory of probability, do not neglect the first paragraphs of the article. The point is that without clear understanding basics, you will not be able to work with the formulas discussed below.
So there's some going on random event, some kind of experiment. As a result of the actions we take, we can get several outcomes - some of them occur more often, others less often. The probability of an event is the ratio of the number of actually obtained outcomes of one type to total number possible. Only knowing the classical definition of this concept can you begin to study the mathematical expectation and dispersion of continuous random variables.
Average
Back in school, during math lessons, you started working with the arithmetic mean. This concept is widely used in probability theory, and therefore cannot be ignored. The main thing for us is this moment is that we will encounter it in the formulas for the mathematical expectation and dispersion of a random variable.

We have a sequence of numbers and want to find the arithmetic mean. All that is required of us is to sum up everything available and divide by the number of elements in the sequence. Let us have numbers from 1 to 9. The sum of the elements will be equal to 45, and we will divide this value by 9. Answer: - 5.
Dispersion
In scientific terms, dispersion is the average square of deviations of the obtained values of a characteristic from the arithmetic mean. It is denoted by one capital Latin letter D. What is needed to calculate it? For each element of the sequence, we calculate the difference between the existing number and the arithmetic mean and square it. There will be exactly as many values as there can be outcomes for the event we are considering. Next, we sum up everything received and divide by the number of elements in the sequence. If we have five possible outcomes, then divide by five.

Dispersion also has properties that need to be remembered in order to be used when solving problems. For example, when increasing a random variable by X times, the variance increases by X squared times (i.e. X*X). It is never less than zero and does not depend on shifting values up or down by equal amounts. Additionally, for independent trials, the variance of the sum is equal to the sum of the variances.
Now we definitely need to consider examples of the variance of a discrete random variable and the mathematical expectation.
Let's say we ran 21 experiments and got 7 different outcomes. We observed each of them 1, 2, 2, 3, 4, 4 and 5 times, respectively. What will the variance be equal to?
First, let's calculate the arithmetic mean: the sum of the elements, of course, is 21. Divide it by 7, getting 3. Now subtract 3 from each number in the original sequence, square each value, and add the results together. The result is 12. Now all we have to do is divide the number by the number of elements, and, it would seem, that’s all. But there's a catch! Let's discuss it.
Dependence on the number of experiments
It turns out that when calculating variance, the denominator can contain one of two numbers: either N or N-1. Here N is the number of experiments performed or the number of elements in the sequence (which is essentially the same thing). What does this depend on?

If the number of tests is measured in hundreds, then we must put N in the denominator. If in units, then N-1. Scientists decided to draw the border quite symbolically: today it passes through the number 30. If we conducted less than 30 experiments, then we will divide the amount by N-1, and if more, then by N.
Task
Let's return to our example of solving the problem of variance and mathematical expectation. We got an intermediate number 12, which needed to be divided by N or N-1. Since we conducted 21 experiments, which is less than 30, we will choose the second option. So the answer is: the variance is 12 / 2 = 2.
Expected value
Let's move on to the second concept, which we must consider in this article. Expected value is the result of adding all possible outcomes multiplied by the corresponding probabilities. It is important to understand that the obtained value, as well as the result of calculating the variance, is obtained only once for the entire problem, no matter how many outcomes are considered in it.

The formula for mathematical expectation is quite simple: we take the outcome, multiply it by its probability, add the same for the second, third result, etc. Everything related to this concept is not difficult to calculate. For example, the sum of the expected values is equal to the expected value of the sum. The same is true for the work. Such simple operations Not every quantity in probability theory allows you to do this. Let's take the problem and calculate the meaning of two concepts we have studied at once. Besides, we were distracted by theory - it's time to practice.
One more example
We ran 50 trials and got 10 types of outcomes - numbers from 0 to 9 - appearing in different percentages. These are, respectively: 2%, 10%, 4%, 14%, 2%,18%, 6%, 16%, 10%, 18%. Recall that to obtain probabilities, you need to divide the percentage values by 100. Thus, we get 0.02; 0.1, etc. Let us present an example of solving the problem for the variance of a random variable and the mathematical expectation.
We calculate the arithmetic mean using the formula that we remember from junior school: 50/10 = 5.
Now let’s convert the probabilities into the number of outcomes “in pieces” to make it easier to count. We get 1, 5, 2, 7, 1, 9, 3, 8, 5 and 9. From each value obtained, we subtract the arithmetic mean, after which we square each of the results obtained. See how to do this using the first element as an example: 1 - 5 = (-4). Next: (-4) * (-4) = 16. For other values, do these operations yourself. If you did everything correctly, then after adding them all up you will get 90.

Let's continue calculating the variance and expected value by dividing 90 by N. Why do we choose N rather than N-1? Correct, because the number of experiments performed exceeds 30. So: 90/10 = 9. We got the variance. If you get a different number, don't despair. Most likely, you made a simple mistake in the calculations. Double-check what you wrote, and everything will probably fall into place.
Finally, remember the formula for mathematical expectation. We will not give all the calculations, we will only write an answer that you can check with after completing all the required procedures. The expected value will be 5.48. Let us only recall how to carry out operations, using the first elements as an example: 0*0.02 + 1*0.1... and so on. As you can see, we simply multiply the outcome value by its probability.
Deviation
Another concept closely related to dispersion and mathematical expectation is average. standard deviation. It is designated either with Latin letters sd, or Greek lowercase "sigma". This concept shows how much on average the values deviate from central feature. To find its value, you need to calculate Square root from dispersion.

If you plot a normal distribution graph and want to see the squared deviation directly on it, this can be done in several stages. Take half of the image to the left or right of the fashion ( central importance), draw a perpendicular to the horizontal axis so that the areas of the resulting figures are equal. The size of the segment between the middle of the distribution and the resulting projection onto the horizontal axis will represent the standard deviation.
Software
As can be seen from the descriptions of the formulas and the examples presented, calculating variance and mathematical expectation is not the simplest procedure from an arithmetic point of view. In order not to waste time, it makes sense to use the program used in higher education educational institutions- it's called "R". It has functions that allow you to calculate values for many concepts from statistics and probability theory.
For example, you specify a vector of values. This is done as follows: vector<-c(1,5,2…). Теперь, когда вам потребуется посчитать какие-либо значения для этого вектора, вы пишете функцию и задаете его в качестве аргумента. Для нахождения дисперсии вам нужно будет использовать функцию var. Пример её использования: var(vector). Далее вы просто нажимаете «ввод» и получаете результат.
Finally
Dispersion and mathematical expectation are without which it is difficult to calculate anything in the future. In the main course of lectures at universities, they are discussed already in the first months of studying the subject. It is precisely because of the lack of understanding of these simple concepts and the inability to calculate them that many students immediately begin to fall behind in the program and later receive bad grades at the end of the session, which deprives them of scholarships.
Practice for at least one week, half an hour a day, solving tasks similar to those presented in this article. Then, on any test in probability theory, you will be able to cope with the examples without extraneous tips and cheat sheets.
The mathematical expectation is the average value of a random variable.The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and their probabilities:
Example.
X -4 6 10
р 0.2 0.3 0.5
Solution: The mathematical expectation is equal to the sum of the products of all possible values of X and their probabilities:
M (X) = 4*0.2 + 6*0.3 +10*0.5 = 6.
To calculate the mathematical expectation, it is convenient to carry out calculations in Excel (especially when there is a lot of data), we suggest using a ready-made template ().
An example for solving it yourself (you can use a calculator).
Find the mathematical expectation of a discrete random variable X specified by the distribution law:
X 0.21 0.54 0.61
р 0.1 0.5 0.4
The mathematical expectation has the following properties.
Property 1. The mathematical expectation of a constant value is equal to the constant itself: M(C)=C.
Property 2. The constant factor can be taken out as a sign of the mathematical expectation: M(CX)=CM(X).
Property 3. The mathematical expectation of the product of mutually independent random variables is equal to the product of the mathematical expectations of the factors: M (X1X2 ...Xn) = M (X1) M (X2)*. ..*M (Xn)
Property 4. The mathematical expectation of the sum of random variables is equal to the sum of the mathematical expectations of the terms: M(Xg + X2+...+Xn) = M(Xg)+M(X2)+...+M(Xn).
Problem 189. Find the mathematical expectation of the random variable Z if the mathematical expectations of X and Y are known: Z = X+2Y, M(X) = 5, M(Y) = 3;
Solution: Using the properties of the mathematical expectation (the mathematical expectation of the sum is equal to the sum of the mathematical expectations of the terms; the constant factor can be taken out of the sign of the mathematical expectation), we obtain M(Z)=M(X + 2Y)=M(X) + M(2Y)=M (X) + 2M(Y)= 5 + 2*3 = 11.
190. Using the properties of mathematical expectation, prove that: a) M(X - Y) = M(X) - M (Y); b) the mathematical expectation of the deviation X-M(X) is equal to zero.
191. A discrete random variable X takes three possible values: x1= 4 With probability p1 = 0.5; xЗ = 6 With probability P2 = 0.3 and x3 with probability p3. Find: x3 and p3, knowing that M(X)=8.
192. A list of possible values of a discrete random variable X is given: x1 = -1, x2 = 0, x3= 1; the mathematical expectations of this value and its square are also known: M(X) = 0.1, M(X^2) = 0 ,9. Find the probabilities p1, p2, p3 corresponding to the possible values of xi
194. A batch of 10 parts contains three non-standard parts. Two parts were selected at random. Find the mathematical expectation of a discrete random variable X - the number of non-standard parts among two selected ones.
196. Find the mathematical expectation of a discrete random variable X-number of such throws of five dice, in each of which one point will appear on two dice, if the total number of throws is twenty.
The mathematical expectation of a binomial distribution is equal to the number of trials multiplied by the probability of an event occurring in one trial:
The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and their probabilities.
Let a random variable take only probability values which are respectively equal. Then the mathematical expectation of a random variable is determined by the equality
If a discrete random variable takes a countable set of possible values, then
Moreover, the mathematical expectation exists if the series on the right side of the equality converges absolutely.
Comment. From the definition it follows that the mathematical expectation of a discrete random variable is a non-random (constant) quantity.
Definition of mathematical expectation in the general case
Let us determine the mathematical expectation of a random variable whose distribution is not necessarily discrete. Let's start with the case of non-negative random variables. The idea will be to approximate such random variables using discrete ones for which the mathematical expectation has already been determined, and set the mathematical expectation equal to the limit of the mathematical expectations of the discrete random variables that approximate it. By the way, this is a very useful general idea, which is that some characteristic is first determined for simple objects, and then for more complex objects it is determined by approximating them by simpler ones.
Lemma 1. Let there be an arbitrary non-negative random variable. Then there is a sequence of discrete random variables such that

Proof. Let us divide the semi-axis into equal length segments and determine
Then properties 1 and 2 easily follow from the definition of a random variable, and
Lemma 2. Let be a non-negative random variable and and two sequences of discrete random variables possessing properties 1-3 from Lemma 1. Then
Proof. Note that for non-negative random variables we allow
By virtue of Property 3, it is easy to see that there is a sequence of positive numbers such that
It follows that
Using the properties of mathematical expectations for discrete random variables, we obtain
Passing to the limit at we obtain the statement of Lemma 2.
Definition 1. Let be a non-negative random variable, - a sequence of discrete random variables that have properties 1-3 from Lemma 1. The mathematical expectation of a random variable is the number
Lemma 2 guarantees that it does not depend on the choice of approximating sequence.
Let now be an arbitrary random variable. Let's define


From the definition and it easily follows that

Definition 2. The mathematical expectation of an arbitrary random variable is the number
If at least one of the numbers on the right side of this equality is finite.
Properties of mathematical expectation
Property 1. The mathematical expectation of a constant value is equal to the constant itself:
Proof. We will consider a constant as a discrete random variable that has one possible value and takes it with probability, therefore,
Remark 1. Let us define the product of a constant variable by a discrete random variable as a discrete random whose possible values are equal to the products of the constant by the possible values; the probabilities of possible values are equal to the probabilities of the corresponding possible values. For example, if the probability of a possible value is equal then the probability that the value will take the value is also equal
Property 2. The constant factor can be taken out of the sign of the mathematical expectation:
Proof. Let the random variable be given by the probability distribution law:
Taking into account Remark 1, we write the distribution law of the random variable
Remark 2. Before moving on to the next property, we point out that two random variables are called independent if the distribution law of one of them does not depend on what possible values the other variable took. Otherwise, the random variables are dependent. Several random variables are called mutually independent if the laws of distribution of any number of them do not depend on what possible values the remaining variables took.
Remark 3. Let us define the product of independent random variables and as a random variable whose possible values are equal to the products of each possible value by each possible value, the probabilities of the possible values of the product are equal to the products of the probabilities of the possible values of the factors. For example, if the probability of a possible value is, the probability of a possible value is then the probability of a possible value is
Property 3. The mathematical expectation of the product of two independent random variables is equal to the product of their mathematical expectations:
Proof. Let independent random variables be specified by their own probability distribution laws:
Let's compile all the values that a random variable can take. To do this, let's multiply all possible values by each possible value; As a result, we obtain and, taking into account Remark 3, we write the distribution law, assuming for simplicity that all possible values of the product are different (if this is not the case, then the proof is carried out in a similar way):
The mathematical expectation is equal to the sum of the products of all possible values and their probabilities:
Consequence. The mathematical expectation of the product of several mutually independent random variables is equal to the product of their mathematical expectations.
Property 4. The mathematical expectation of the sum of two random variables is equal to the sum of the mathematical expectations of the terms:
Proof. Let random variables and be specified by the following distribution laws:
Let's compile all possible values of a quantity. To do this, we add each possible value to each possible value; we obtain. Let us assume for simplicity that these possible values are different (if this is not the case, then the proof is carried out in a similar way), and we denote their probabilities, respectively, by and
The mathematical expectation of a value is equal to the sum of the products of possible values and their probabilities:
Let us prove that an Event that will take on the value (the probability of this event is equal) entails an event that will take on the value or (the probability of this event by the addition theorem is equal), and vice versa. Hence it follows that the equalities are proved similarly
Substituting the right-hand sides of these equalities into relation (*), we obtain
or finally
Variance and standard deviation
In practice, it is often necessary to estimate the dispersion of possible values of a random variable around its mean value. For example, in artillery it is important to know how closely the shells will fall near the target that is to be hit.
At first glance, it may seem that the easiest way to estimate dispersion is to calculate all possible deviations of a random variable and then find their average value. However, this path will not give anything, since the average value of the deviation, i.e. for any random variable is equal to zero. This property is explained by the fact that some possible deviations are positive, while others are negative; as a result of their mutual cancellation, the average deviation value is zero. These considerations indicate the advisability of replacing possible deviations with their absolute values or their squares. This is what they do in practice. True, in the case when possible deviations are replaced by absolute values, one has to operate with absolute values, which sometimes leads to serious difficulties. Therefore, most often they take a different path, i.e. calculate the average value of the squared deviation, which is called dispersion.
Expectation and variance are the most commonly used numerical characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of scattering. In many practical problems, a complete, exhaustive characteristic of a random variable - the distribution law - either cannot be obtained at all, or is not needed at all. In these cases, one is limited to an approximate description of a random variable using numerical characteristics.
The expected value is often called simply the average value of a random variable. Dispersion of a random variable is a characteristic of dispersion, the spread of a random variable around its mathematical expectation.
Expectation of a discrete random variable
Let us approach the concept of mathematical expectation, first based on the mechanical interpretation of the distribution of a discrete random variable. Let the unit mass be distributed between the points of the x-axis x1 , x 2 , ..., x n, and each material point has a corresponding mass of p1 , p 2 , ..., p n. It is required to select one point on the abscissa axis, characterizing the position of the entire system of material points, taking into account their masses. It is natural to take the center of mass of the system of material points as such a point. This is the weighted average of the random variable X, to which the abscissa of each point xi enters with a “weight” equal to the corresponding probability. The average value of the random variable obtained in this way X is called its mathematical expectation.
The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and the probabilities of these values:

Example 1. A win-win lottery has been organized. There are 1000 winnings, of which 400 are 10 rubles. 300 - 20 rubles each. 200 - 100 rubles each. and 100 - 200 rubles each. What is the average winnings for someone who buys one ticket?
Solution. We will find the average winnings if we divide the total amount of winnings, which is 10*400 + 20*300 + 100*200 + 200*100 = 50,000 rubles, by 1000 (total amount of winnings). Then we get 50000/1000 = 50 rubles. But the expression for calculating the average winnings can be presented in the following form:
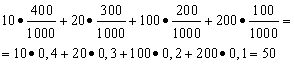
On the other hand, in these conditions, the winning size is a random variable, which can take values of 10, 20, 100 and 200 rubles. with probabilities equal to 0.4, respectively; 0.3; 0.2; 0.1. Therefore, the expected average win is equal to the sum of the products of the size of the wins and the probability of receiving them.
Example 2. The publisher decided to publish a new book. He plans to sell the book for 280 rubles, of which he himself will receive 200, 50 - the bookstore and 30 - the author. The table provides information about the costs of publishing a book and the probability of selling a certain number of copies of the book.
Find the publisher's expected profit.
Solution. The random variable “profit” is equal to the difference between the income from sales and the cost of costs. For example, if 500 copies of a book are sold, then the income from the sale is 200 * 500 = 100,000, and the cost of publication is 225,000 rubles. Thus, the publisher faces a loss of 125,000 rubles. The following table summarizes the expected values of the random variable - profit:
| Number | Profit xi | Probability pi | xi p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Total: | 1,00 | 25000 |
Thus, we obtain the mathematical expectation of the publisher’s profit:
![]() .
.
Example 3. Probability of hitting with one shot p= 0.2. Determine the consumption of projectiles that provide a mathematical expectation of the number of hits equal to 5.
Solution. From the same mathematical expectation formula that we have used so far, we express x- shell consumption:
![]() .
.
Example 4. Determine the mathematical expectation of a random variable x number of hits with three shots, if the probability of a hit with each shot p = 0,4 .
Hint: find the probability of random variable values by Bernoulli's formula .
Properties of mathematical expectation
Let's consider the properties of mathematical expectation.
Property 1. The mathematical expectation of a constant value is equal to this constant:
Property 2. The constant factor can be taken out of the mathematical expectation sign:
![]()
Property 3. The mathematical expectation of the sum (difference) of random variables is equal to the sum (difference) of their mathematical expectations:
Property 4. The mathematical expectation of a product of random variables is equal to the product of their mathematical expectations:
Property 5. If all values of a random variable X decrease (increase) by the same number WITH, then its mathematical expectation will decrease (increase) by the same number:
![]()
When you can’t limit yourself only to mathematical expectation
In most cases, only the mathematical expectation cannot sufficiently characterize a random variable.
Let the random variables X And Y are given by the following distribution laws:
| Meaning X | Probability |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Meaning Y | Probability |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
The mathematical expectations of these quantities are the same - equal to zero:
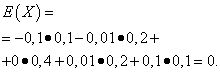

However, their distribution patterns are different. Random value X can only take values that differ little from the mathematical expectation, and the random variable Y can take values that deviate significantly from the mathematical expectation. A similar example: the average wage does not make it possible to judge the share of high- and low-paid workers. In other words, one cannot judge from the mathematical expectation what deviations from it, at least on average, are possible. To do this, you need to find the variance of the random variable.
Variance of a discrete random variable
Variance discrete random variable X is called the mathematical expectation of the square of its deviation from the mathematical expectation:
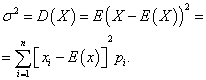
The standard deviation of a random variable X the arithmetic value of the square root of its variance is called:
![]() .
.
Example 5. Calculate variances and standard deviations of random variables X And Y, the distribution laws of which are given in the tables above.
Solution. Mathematical expectations of random variables X And Y, as found above, are equal to zero. According to the dispersion formula at E(X)=E(y)=0 we get:

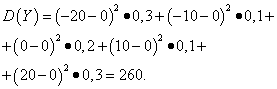
Then the standard deviations of random variables X And Y make up
![]() .
.
Thus, with the same mathematical expectations, the variance of the random variable X very small, but a random variable Y- significant. This is a consequence of differences in their distribution.
Example 6. The investor has 4 alternative investment projects. The table summarizes the expected profit in these projects with the corresponding probability.
| Project 1 | Project 2 | Project 3 | Project 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Find the mathematical expectation, variance and standard deviation for each alternative.
Solution. Let us show how these values are calculated for the 3rd alternative:
The table summarizes the found values for all alternatives.
All alternatives have the same mathematical expectations. This means that in the long run everyone has the same income. Standard deviation can be interpreted as a measure of risk - the higher it is, the greater the risk of the investment. An investor who does not want much risk will choose project 1 since it has the smallest standard deviation (0). If an investor prefers risk and high returns in a short period, then he will choose the project with the largest standard deviation- project 4.
Dispersion properties
Let us present the properties of dispersion.
Property 1. The variance of a constant value is zero:
Property 2. The constant factor can be taken out of the dispersion sign by squaring it:
![]() .
.
Property 3. The variance of a random variable is equal to the mathematical expectation of the square of this value, from which the square of the mathematical expectation of the value itself is subtracted:
![]() ,
,
Where ![]() .
.
Property 4. The variance of the sum (difference) of random variables is equal to the sum (difference) of their variances:
Example 7. It is known that a discrete random variable X takes only two values: −3 and 7. In addition, the mathematical expectation is known: E(X) = 4 . Find the variance of a discrete random variable.
Solution. Let us denote by p the probability with which a random variable takes a value x1 = −3 . Then the probability of the value x2 = 7 will be 1 − p. Let us derive the equation for the mathematical expectation:
E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,
where we get the probabilities: p= 0.3 and 1 − p = 0,7 .
Law of distribution of a random variable:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
We calculate the variance of this random variable using the formula from property 3 of dispersion:
D(X) = 2,7 + 34,3 − 16 = 21 .
Find the mathematical expectation of a random variable yourself, and then look at the solution
Example 8. Discrete random variable X takes only two values. It accepts the greater of the values 3 with probability 0.4. In addition, the variance of the random variable is known D(X) = 6 . Find the mathematical expectation of a random variable.
Example 9. There are 6 white and 4 black balls in an urn. 3 balls are drawn from the urn. The number of white balls among the drawn balls is a discrete random variable X. Find the mathematical expectation and variance of this random variable.
Solution. Random value X can take values 0, 1, 2, 3. The corresponding probabilities can be calculated from probability multiplication rule. Law of distribution of a random variable:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Hence the mathematical expectation of this random variable:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
The variance of a given random variable is:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Expectation and variance of a continuous random variable
For a continuous random variable, the mechanical interpretation of the mathematical expectation will retain the same meaning: the center of mass for a unit mass distributed continuously on the x-axis with density f(x). Unlike a discrete random variable, whose function argument xi changes abruptly; for a continuous random variable, the argument changes continuously. But the mathematical expectation of a continuous random variable is also related to its average value.
To find the mathematical expectation and variance of a continuous random variable, you need to find definite integrals . If the density function of a continuous random variable is given, then it directly enters into the integrand. If a probability distribution function is given, then by differentiating it, you need to find the density function.
The arithmetic average of all possible values of a continuous random variable is called its mathematical expectation, denoted by or .
The mathematical expectation of a random variable X is the mean value.
1. M(C) = C
2. M(CX) = CM(X), Where C= const
3. M(X ± Y) = M(X) ± M(Y)
4. If random variables X And Y are independent, then M(XY) = M(X) M(Y)
Dispersion
The variance of a random variable X is called
D(X) = S(x – M(X)) 2 p = M(X 2 ) – M 2 (X).
Dispersion is a measure of the deviation of the values of a random variable from its mean value.
1. D(C) = 0
2. D(X + C) = D(X)
3. D(CX) = C 2 D(X), Where C= const
4. For independent random variables
D(X ± Y) = D(X) + D(Y)
5. D(X ± Y) = D(X) + D(Y) ± 2Cov(x, y)
The square root of the variance of a random variable X is called the standard deviation ![]() .
.
@Task 3: Let the random variable X take only two values (0 or 1) with probabilities q, p, Where p + q = 1. Find the mathematical expectation and variance.
Solution:
M(X) = 1 p + 0 q = p; D(X) = (1 – p) 2 p + (0 – p) 2 q = pq.
@Task 4: Expectation and variance of a random variable X are equal to 8. Find the mathematical expectation and variance of random variables: a) X – 4; b) 3X – 4.
Solution: M(X – 4) = M(X) – 4 = 8 – 4 = 4; D(X – 4) = D(X) = 8; M(3X – 4) = 3M(X) – 4 = 20; D(3X – 4) = 9D(X) = 72.
@Task 5: The totality of families has the following distribution by number of children:
| x i | x 1 | x 2 | ||
| p i | 0,1 | p2 | 0,4 | 0,35 |
Define x 1, x 2 And p2, if it is known that M(X) = 2; D(X) = 0.9.
Solution: Probability p 2 is equal to p 2 = 1 – 0.1 – 0.4 – 0.35 = 0.15. The unknown x are found from the equations: M(X) = x 1 ·0.1 + x 2 ·0.15 + 2·0.4 + 3·0.35 = 2; D(X) = ·0.1 + ·0.15 + 4·0.4 + 9·0.35 – 4 = 0.9. x 1 = 0; x 2 = 1.
Population and sample. Parameter estimates
Selective observation
Statistical observation can be organized continuous or not continuous. Continuous observation involves examining all units of the population being studied ( population). Population this is a set of individuals or legal entities that the researcher studies according to his task. This is often not economically viable and sometimes impossible. In this regard, only part of the general population is studied - sample population .
The results obtained from a sample population can be extended to the general population if the following principles are followed:
1. The sample population must be determined randomly.
2. The number of units in the sample population must be sufficient.
3. Must be provided representativeness ( representativeness) of the sample. A representative sample is a smaller but accurate model of the population it is intended to reflect.
Sample types
The following types of samples are used in practice:
a) strictly random, b) mechanical, c) typical, d) serial, e) combined.
Proper random sampling
At actual random sample the selection of units in the sample population is carried out randomly, for example, by drawing lots or using a random number generator.
Samples can be repeated or non-repeated. In resampling, a unit that is sampled is returned and retains an equal opportunity to be sampled again. In non-repetitive sampling, a population unit that is included in the sample does not participate in the sample in the future.
Errors inherent in sampling observation, arising due to the fact that the sample population does not completely reproduce the general population, are called standard errors . They represent the mean square difference between the values of the indicators obtained from the sample and the corresponding values of the indicators of the general population.
The calculation formulas for the standard error for random repeated sampling are as follows: , and for random non-repetitive sampling as follows: ![]() , where S 2 is the variance of the sample population, n/N – sample share, n, N- the number of units in the sample and general population. At n = N standard error m = 0.
, where S 2 is the variance of the sample population, n/N – sample share, n, N- the number of units in the sample and general population. At n = N standard error m = 0.
Mechanical sampling
At mechanical sampling The population is divided into equal intervals and one unit is randomly selected from each interval.
For example, with a 2% sampling rate, every 50th unit is selected from the population list.
The standard error of mechanical sampling is defined as the error of a truly random non-repetitive sampling.
Typical sample
At typical sample the general population is divided into homogeneous typical groups, then units are randomly selected from each group.
A typical sample is used in the case of a heterogeneous population. A typical sample provides more accurate results because it ensures representativeness.
For example, teachers, as a general population, are divided into groups according to the following criteria: gender, experience, qualifications, education, urban and rural schools, etc.
Standard errors of a typical sample are defined as errors of a truly random sample, with the only difference that S 2 is replaced by the average of the within-group variances.
Serial sampling
At serial sampling the general population is divided into separate groups (series), then randomly selected groups are subjected to continuous observation.
The standard errors of a serial sample are defined as the errors of a truly random sample, with the only difference being that S 2 is replaced by the average of the between-group variances.
Combined sample
Combined sample is a combination of two or more sample types.
Point estimate
The ultimate goal of sample observation is to find the characteristics of the population. Since this cannot be done directly, the characteristics of the sample population are extended to the general population.
The fundamental possibility of determining the arithmetic mean of the population from the data of the average sample is proven Chebyshev's theorem. With unlimited magnification n the probability that the difference between the sample mean and the general mean will be arbitrarily small tends to 1.
This means that the characteristics of the population with an accuracy of . This assessment is called point .
Interval estimation
The basis of interval estimation is central limit theorem.
Interval estimation allows us to answer the question: within what interval and with what probability is the unknown, desired value of the population parameter located?
Usually we talk about confidence probability p = 1 – a, with which it will be in the interval – D< < + D, где D = t cr m > 0 marginal error samples, a - significance level (probability that the inequality will be false), t cr- critical value, which depends on the values n and a. For a small sample n< 30 t cr is specified using the critical value of the Student t-distribution for a two-sided test with n– 1 degrees of freedom with significance level a ( t cr(n – 1, a) is found from the table “Critical values of Student’s t-distribution”, Appendix 2). For n > 30, t cr- this is a quantile normal law distributions ( t cr is found from the table of values of the Laplace function F(t) = (1 – a)/2 as argument). At p = 0.954 the critical value t cr= 2 at p = 0.997 critical value t cr= 3. This means that the marginal error is usually 2-3 times larger than the standard error.
Thus, the essence of the sampling method is that, based on the statistical data of a certain small part of the population, it is possible to find an interval in which, with a confidence probability p the desired characteristic of the general population is found (average number of workers, average score, average yield, standard deviation, etc.).
@Task 1. To determine the speed of settlements with creditors of corporation enterprises, a random sample of 100 payment documents was carried out in a commercial bank, according to which average term transfer and receipt of money turned out to be 22 days (= 22) with a standard deviation of 6 days (S = 6). With probability p= 0.954 determine the maximum error of the sample average and the confidence interval of the average duration of settlements of the enterprises of this corporation.
Solution: Marginal error of sample average according to(1)equal to D= 2· 0.6 = 1.2, and the confidence interval is defined as (22 – 1.2; 22 + 1.2), i.e. (20.8; 23.2).
§6.5 Correlation and regression


