$X$. Najpierw przypomnijmy następującą definicję:
Definicja 1
Populacja-- zbiór losowo wybranych obiektów danego typu, które obserwuje się w celu uzyskania określonych wartości zmienna losowa prowadzone w stałych warunkach w badaniu jednej zmiennej losowej danego typu.
Definicja 2
Ogólna wariancja-- przeciętny kwadraty arytmetyczne odchylenia wartości wariantu populacji ogólnej od ich średniej wartości.
Niech wartości wariantu $x_1,\ x_2,\dots ,x_k$ mają odpowiednio częstości $n_1,\ n_2,\dots ,n_k$. Następnie ogólna wariancja obliczone według wzoru:
Rozważmy szczególny przypadek. Niech wszystkie warianty $x_1,\ x_2,\dots ,x_k$ będą różne. W tym przypadku $n_1,\ n_2,\dots ,n_k=1$. Otrzymujemy, że w tym przypadku ogólna wariancja jest obliczana według wzoru:
Z tą koncepcją wiąże się również koncepcja ogólnego odchylenia standardowego.
Definicja 3
Średnia ogólna odchylenie standardowe
\[(\sigma )_r=\sqrt(D_r)\]
Przykładowa wariancja
Otrzymamy zbiór próbny ze względu na zmienną losową $X$. Najpierw przypomnijmy następującą definicję:
Definicja 4
Populacja próbna -- część wybranych obiektów z populacji generalnej.
Definicja 5
Przykładowa wariancja-- przeciętny wartości arytmetyczne opcja próbkowania.
Niech wartości wariantu $x_1,\ x_2,\dots ,x_k$ mają odpowiednio częstości $n_1,\ n_2,\dots ,n_k$. Następnie wariancja próby jest obliczana według wzoru:
Rozważmy szczególny przypadek. Niech wszystkie warianty $x_1,\ x_2,\dots ,x_k$ będą różne. W tym przypadku $n_1,\ n_2,\dots ,n_k=1$. Otrzymujemy, że w tym przypadku wariancja próbki jest obliczana według wzoru:
Z tą koncepcją wiąże się również koncepcja odchylenia standardowego próbki.
Definicja 6
Odchylenie standardowe próbki -- Pierwiastek kwadratowy z ogólnej wariancji:
\[(\sigma )_v=\sqrt(D_v)\]
Skorygowana wariancja
Aby znaleźć skorygowaną wariancję $S^2$, należy pomnożyć wariancję próby przez ułamek $\frac(n)(n-1)$, tj.
Pojęcie to jest również związane z pojęciem skorygowanego odchylenia standardowego, które można znaleźć za pomocą wzoru:
W przypadku, gdy wartość wariantu nie jest dyskretna, lecz przedziałowa, to we wzorach do obliczania wariancji ogólnej lub z próby wartość $x_i$ przyjmuje się jako wartość środka przedziału, do którego $ x_i.$ należy
Przykład problemu znalezienia wariancji i odchylenia standardowego
Przykład 1
Populacja próby jest przedstawiona w następującej tabeli rozkładu:
Obrazek 1.
Znajdź dla niej wariancję próbki, odchylenie standardowe próbki, skorygowaną wariancję i skorygowane odchylenie standardowe.
Aby rozwiązać ten problem, najpierw stworzymy tabelę obliczeniową:
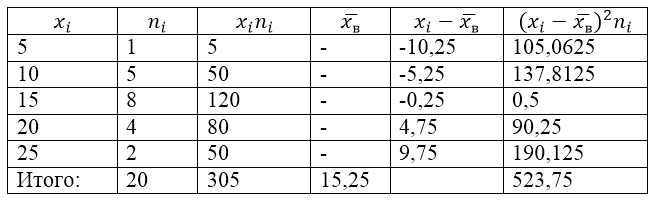
Rysunek 2.
Wartość $\overline(x_v)$ (średnia z próby) w tabeli znajduje się na podstawie wzoru:
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15.25\]
Znajdź wariancję próbki za pomocą wzoru:
Odchylenie standardowe próbki:
\[(\sigma )_v=\sqrt(D_v)\około 5,12\]
Skorygowana wariancja:
\[(S^2=\frac(n)(n-1)D)_v=\frac(20)(19)\cdot 26,1875\około 27,57\]
Skorygowane odchylenie standardowe.
Program Excel jest wysoko ceniony zarówno przez profesjonalistów, jak i amatorów, ponieważ może z nim pracować użytkownik na każdym poziomie wyszkolenia. Na przykład każdy, kto ma minimalne umiejętności „komunikacji” z Excelem, może narysować prosty wykres, zrobić porządny znak itp.
Jednocześnie ten program pozwala nawet na wykonywanie różnego rodzaju obliczeń, na przykład obliczeń, ale to już wymaga nieco innego poziomu wyszkolenia. Jeśli jednak dopiero zacząłeś bliższą znajomość z tym programem i interesuje Cię wszystko, co pomoże Ci stać się bardziej zaawansowanym użytkownikiem, ten artykuł jest dla Ciebie. Dzisiaj powiem ci, czym jest formuła odchylenia standardowego w programie Excel, dlaczego w ogóle jest potrzebna iw rzeczywistości, kiedy jest stosowana. Iść!
Co to jest
Zacznijmy od teorii. Odchylenie standardowe jest zwykle nazywane pierwiastkiem kwadratowym, otrzymywanym ze średniej arytmetycznej wszystkich kwadratów różnic między dostępnymi wartościami, a także ich średniej arytmetycznej. Nawiasem mówiąc, ta wartość jest zwykle nazywana grecką literą „sigma”. Odchylenie standardowe jest obliczane odpowiednio za pomocą wzoru ODCH.STANDARDOWE, program robi to za samego użytkownika.
Istotą tej koncepcji jest określenie stopnia zmienności instrumentu, czyli jest on na swój sposób wskaźnikiem ze statystyki opisowej. Ujawnia zmiany zmienności instrumentu w dowolnym okresie czasu. Korzystając ze wzorów STDEV, możesz oszacować odchylenie standardowe podczas pobierania, podczas gdy wartości logiczne i tekstowe są ignorowane.
Formuła
Pomaga obliczyć odchylenie standardowe w formuła excela, który jest automatycznie dostarczany w programie Excela. Aby go znaleźć, musisz znaleźć sekcję formuły w Excelu i już tam wybrać tę, która ma nazwę STDEV, więc jest to bardzo proste.
Następnie pojawi się przed tobą okno, w którym będziesz musiał wprowadzić dane do obliczeń. W szczególności należy wpisać w specjalne pola dwie liczby, po których program automatycznie obliczy odchylenie standardowe dla próbki.

Niewątpliwie wzory i obliczenia matematyczne są dość skomplikowanym zagadnieniem i nie wszyscy użytkownicy mogą sobie z tym poradzić od razu. Jeśli jednak pogrzebiesz trochę głębiej i zrozumiesz problem nieco bardziej szczegółowo, okaże się, że nie wszystko jest takie smutne. Mam nadzieję, że przekonałeś się o tym na przykładzie obliczania odchylenia standardowego.
Wideo, aby pomóc
Mądrzejsi matematycy i statystycy wymyślili bardziej wiarygodny wskaźnik, choć w nieco innym celu - przeciętny odchylenie liniowe . Wskaźnik ten charakteryzuje miarę rozrzutu wartości zbioru danych wokół ich średniej wartości.
Aby pokazać miarę rozrzutu danych, należy najpierw ustalić, względem czego ten rozrzut będzie rozpatrywany – zazwyczaj jest to wartość średnia. Następnie musisz obliczyć, jak daleko wartości analizowanego zbioru danych są dalekie od średniej. Oczywiste jest, że każda wartość odpowiada pewnej wielkości odchylenia, ale jesteśmy również zainteresowani ogólnym oszacowaniem obejmującym całą populację. Dlatego średnie odchylenie oblicza się za pomocą wzoru zwykłej średniej arytmetycznej. Ale! Ale aby obliczyć średnią odchyleń, należy je najpierw dodać. A jeśli dodamy liczby dodatnie i ujemne, zniosą się one wzajemnie, a ich suma będzie dążyć do zera. Aby tego uniknąć, wszystkie odchylenia są przyjmowane modulo, to znaczy wszystkie liczby ujemne stają się dodatnie. Teraz średnie odchylenie pokaże uogólnioną miarę rozrzutu wartości. W rezultacie średnie odchylenie liniowe zostanie obliczone według wzoru:
A to średnie odchylenie liniowe,
X- analizowany wskaźnik, z kreską u góry - wartość średnia wskaźnika,
N to liczba wartości w analizowanym zbiorze danych,
operator sumowania, mam nadzieję, nikogo nie przeraża.
Średnie odchylenie liniowe obliczone za pomocą podanego wzoru odzwierciedla średnie bezwzględne odchylenie od wartości średniej dla tej populacji.

Czerwona linia na obrazku to wartość średnia. Odchylenia każdej obserwacji od średniej zaznaczono małymi strzałkami. Są one brane modulo i sumowane. Następnie wszystko jest dzielone przez liczbę wartości.
Aby obraz był pełny, należy podać jeszcze jeden przykład. Załóżmy, że istnieje firma, która produkuje sadzonki do łopat. Każde cięcie powinno mieć 1,5 metra długości, ale co ważniejsze, wszystkie powinny być takie same lub przynajmniej plus minus 5 cm. Jednak niedbali pracownicy odrąbią 1,2 m, a następnie 1,8 m. . Dyrektor firmy postanowił przeprowadzić analizę statystyczną długości sadzonek. Wybrałem 10 sztuk i zmierzyłem ich długość, znalazłem średnią i obliczyłem średnie odchylenie liniowe. Średnia okazała się odpowiednia - 1,5 m. Ale średnie odchylenie liniowe okazało się 0,16 m. Okazuje się więc, że każde cięcie jest dłuższe lub krótsze niż to konieczne średnio o 16 cm. Jest o czym mówić z robotnikami. W rzeczywistości nie widziałem rzeczywistego zastosowania tego wskaźnika, więc sam wymyśliłem przykład. Jednak w statystykach jest taki wskaźnik.
Dyspersja
Podobnie jak średnie odchylenie liniowe, wariancja odzwierciedla również zakres, w jakim dane rozchodzą się wokół średniej.
Wzór na obliczenie wariancji wygląda następująco:
 (dla serii zmienności (wariancja ważona))
(dla serii zmienności (wariancja ważona))
 (dla danych niezgrupowanych (prosta wariancja))
(dla danych niezgrupowanych (prosta wariancja))
gdzie: σ 2 - dyspersja, Xi– analizujemy wskaźnik sq (wartość cechy), – średnią wartość wskaźnika, f i – liczbę wartości w analizowanym zbiorze danych.
Wariancja to średni kwadrat odchyleń.
Najpierw obliczana jest średnia, następnie pobierana jest różnica między każdą linią bazową a średnią, podnoszona do kwadratu, mnożona przez częstotliwość odpowiedniej wartości cechy, dodawana, a następnie dzielona przez liczbę wartości w populacji.
Jednak w czysta forma, takich jak średnia arytmetyczna lub indeks, wariancja nie jest używana. Jest to raczej wskaźnik pomocniczy i pośredni, który jest używany do innych rodzajów analiz statystycznych.
Uproszczony sposób obliczania wariancji
![]()
odchylenie standardowe
Aby wykorzystać wariancję do analizy danych, pobiera się z niej pierwiastek kwadratowy. Okazuje się, że tzw odchylenie standardowe.

Nawiasem mówiąc, odchylenie standardowe jest również nazywane sigma - od greckiej litery, która to oznacza.
Odchylenie standardowe charakteryzuje oczywiście również miarę rozproszenia danych, ale teraz (w przeciwieństwie do dyspersji) można je porównać z danymi pierwotnymi. Z reguły wskaźniki średniokwadratowe w statystyce dają dokładniejsze wyniki niż liniowe. Dlatego odchylenie standardowe jest dokładniejszą miarą rozproszenia danych niż średnie odchylenie liniowe.
odchylenie standardowe(synonimy: odchylenie standardowe, odchylenie standardowe, odchylenie standardowe; terminy pokrewne: odchylenie standardowe, standardowy spread) - w teorii prawdopodobieństwa i statystyce najczęstszy wskaźnik rozrzutu wartości zmiennej losowej względem jej matematycznego oczekiwania. Przy ograniczonych tablicach próbek wartości, zamiast matematycznej wartości oczekiwanej, używana jest średnia arytmetyczna zbioru próbek.
Encyklopedyczny YouTube
-
1 / 5
Odchylenie standardowe mierzone jest w jednostkach miary samej zmiennej losowej i jest wykorzystywane przy obliczaniu błędu standardowego średniej arytmetycznej, przy konstruowaniu przedziałów ufności, przy statystycznej weryfikacji hipotez, przy pomiarze zależności liniowej między zmiennymi losowymi. Jest zdefiniowany jako pierwiastek kwadratowy z wariancji zmiennej losowej.
Odchylenie standardowe:
s = n n - 1 σ 2 = 1 n - 1 ∑ ja = 1 n (x ja - x ¯) 2 ; (\ Displaystyle s = (\ sqrt ((\ frac (n) (n-1)) \ sigma ^ (2))) = (\ sqrt ((\ frac (1) (n-1)) \ suma _ ( i=1)^(n)\left(x_(i)-(\bar (x))\right)^(2)));)- Uwaga: Bardzo często występują rozbieżności w nazwach RMS (odchylenie standardowe) i SRT (odchylenie standardowe) z ich wzorami. Na przykład w module numPy języka programowania Python funkcja std() jest opisana jako „odchylenie standardowe”, podczas gdy formuła odzwierciedla odchylenie standardowe (podzielone przez pierwiastek próbki). W programie Excel funkcja STDEV() jest inna (dzielenie przez pierwiastek kwadratowy z n-1).
Odchylenie standardowe(oszacowanie odchylenia standardowego zmiennej losowej X względem jego matematycznego oczekiwania opartego na obiektywnym oszacowaniu jego wariancji) s (\ displaystyle s):
σ = 1 n ∑ ja = 1 n (x ja - x ¯) 2 . (\ Displaystyle \ sigma = (\ sqrt ((\ frac (1) (n)) \ suma _ (i = 1) ^ (n) \ lewo (x_ (i) - (\ bar (x)) \ prawo) ^(2))).)Gdzie σ 2 (\ Displaystyle \ sigma ^ (2))- dyspersja ; x ja (\ displaystyle x_ (i)) - I-ty element próbki; n (\ displaystyle n)- wielkość próbki; - średnia arytmetyczna próbki:
x ¯ = 1 n ∑ ja = 1 n x ja = 1 n (x 1 + … + x n) . (\ Displaystyle (\ bar (x)) = (\ frac (1) (n)) \ suma _ (i = 1) ^ (n) x_ (i) = (\ frac (1) (n)) (x_ (1)+\ldkropki +x_(n)).)Należy zauważyć, że oba szacunki są obciążone. W ogólnym przypadku niemożliwe jest skonstruowanie obiektywnego oszacowania. Jednak oszacowanie oparte na nieobciążonym oszacowaniu wariancji jest spójne.
Zgodnie z GOST R 8.736-2011 odchylenie standardowe oblicza się zgodnie z drugim wzorem tej sekcji. Sprawdź swoje wyniki.
reguła trzech sigma
reguła trzech sigma (3 σ (\ displaystyle 3 \ sigma)) - prawie wszystkie wartości zmiennej losowej o rozkładzie normalnym leżą w przedziale (x ¯ - 3 σ; x ¯ + 3 σ) (\ Displaystyle \ lewo ((\ bar (x)) -3 \ sigma; (\ bar (x)) + 3 \ sigma \ prawo)). Ściślej - w przybliżeniu z prawdopodobieństwem 0,9973 wartość zmiennej losowej o rozkładzie normalnym mieści się w określonym przedziale (pod warunkiem, że wartość x Ż (\ Displaystyle (\ bar (x))) prawdziwe, a nie uzyskane w wyniku przetworzenia próbki).
Jeśli prawdziwa wartość x Ż (\ Displaystyle (\ bar (x))) nieznany, powinieneś użyć σ (\ Displaystyle \ sigma), A S. W ten sposób reguła trzech sigma zostaje przekształcona w regułę trzech S .
Interpretacja wartości odchylenia standardowego
Większa wartość odchylenia standardowego wskazuje na większy rozrzut wartości w prezentowanym zbiorze ze średnią zbioru; odpowiednio mniejsza wartość wskazuje, że wartości w zbiorze są zgrupowane wokół wartości średniej.
Na przykład mamy trzy zestawy liczb: (0, 0, 14, 14), (0, 6, 8, 14) i (6, 6, 8, 8). Wszystkie trzy zestawy mają wartości średnie 7 i odchylenia standardowe odpowiednio 7, 5 i 1. Ostatni zestaw ma małe odchylenie standardowe, ponieważ wartości w zestawie są skupione wokół średniej; pierwszy zestaw ma najwięcej bardzo ważne odchylenie standardowe – wartości w obrębie zbioru silnie odbiegają od wartości średniej.
W ogólnym sensie odchylenie standardowe można uznać za miarę niepewności. Na przykład w fizyce odchylenie standardowe służy do określenia błędu serii kolejnych pomiarów pewnej wielkości. Ta wartość jest bardzo ważna dla określenia prawdopodobieństwa badanego zjawiska w porównaniu z wartością przewidywaną przez teorię: jeśli średnia wartość pomiarów bardzo różni się od wartości przewidywanych przez teorię (duże odchylenie standardowe), to uzyskane wartości lub sposób ich uzyskania należy ponownie sprawdzić. jest utożsamiany z ryzykiem portfela.
Klimat
Załóżmy, że istnieją dwa miasta o tej samej średniej maksymalnej temperaturze dziennej, ale jedno znajduje się na wybrzeżu, a drugie na równinie. Wiadomo, że miasta przybrzeżne mają wiele różnych dziennych maksymalnych temperatur niższych niż miasta śródlądowe. W związku z tym odchylenie standardowe maksymalnych temperatur dobowych w mieście nadmorskim będzie mniejsze niż w drugim mieście, mimo że mają one taką samą średnią wartość tej wartości, co w praktyce oznacza, że prawdopodobieństwo, że maksymalna temperatura powietrza w każdego dnia w roku będą silniejsze odbiegać od wartości średniej, wyższej dla miasta położonego w głębi kontynentu.
Sport
Załóżmy, że istnieje kilka drużyn piłkarskich, które są uszeregowane według pewnego zestawu parametrów, na przykład liczby strzelonych i straconych bramek, szans na zdobycie bramki itp. Najprawdopodobniej najlepsza drużyna w tej grupie będzie miała najlepsze wartości w więcej parametrów. Im mniejsze odchylenie standardowe zespołu dla każdego z przedstawionych parametrów, tym bardziej przewidywalny jest wynik zespołu, takie zespoły są zrównoważone. Z kolei zespół z Świetna cena odchylenie standardowe, trudno przewidzieć wynik, co z kolei tłumaczy się brakiem równowagi, np. silna obrona, ale słaby atak.
Zastosowanie odchylenia standardowego parametrów zespołu pozwala w pewnym stopniu przewidzieć wynik meczu pomiędzy dwoma zespołami, oceniając mocne strony i słabe strony rozkazy, a co za tym idzie wybrane metody walki.
Należy zauważyć, że to obliczenie wariancji ma wadę - okazuje się być obciążone, tj. jej wartość oczekiwana nie jest równa prawdziwej wartości wariancji. Więcej informacji na ten temat. Jednocześnie nie wszystko jest takie złe. Wraz ze wzrostem liczebności próby wciąż zbliża się do swojego teoretycznego odpowiednika, tj. jest asymptotycznie nieobciążony. Dlatego podczas pracy z duże rozmiary próbki, możesz użyć powyższego wzoru.
Przydatne jest tłumaczenie języka znaków na język słów. Okazuje się, że wariancja to średni kwadrat odchyleń. Oznacza to, że najpierw obliczana jest wartość średnia, a następnie pobierana jest różnica między każdą wartością pierwotną i średnią, podnoszona do kwadratu, sumowana, a następnie dzielona przez liczbę wartości w tej populacji. Różnica między indywidualną wartością a średnią odzwierciedla miarę odchylenia. Jest podnoszony do kwadratu, aby wszystkie odchylenia stały się wyłącznie liczbami dodatnimi i aby uniknąć wzajemnego znoszenia dodatnich i ujemnych odchyleń podczas ich sumowania. Następnie, biorąc pod uwagę kwadraty odchyleń, po prostu obliczamy średnią arytmetyczną. Średnia - kwadrat - odchylenia. Odchylenia są podnoszone do kwadratu i bierze się pod uwagę średnią. Odpowiedź zawiera się w zaledwie trzech słowach.
Jednak w czystej postaci, takiej jak na przykład średnia arytmetyczna lub wskaźnik, dyspersja nie jest używana. Jest raczej wskaźnikiem pomocniczym i pośrednim, niezbędnym do innych rodzajów analiz statystycznych. Ona nawet nie ma normalnej jednostki miary. Sądząc po wzorze, jest to kwadrat oryginalnej jednostki danych. Bez butelki, jak mówią, nie zrozumiesz.
(moduł 111)
Aby przywrócić dyspersję do rzeczywistości, czyli wykorzystać ją do bardziej przyziemnych celów, wyodrębnia się z niej pierwiastek kwadratowy. Okazuje się, że tzw odchylenie standardowe (RMS). Istnieją nazwy „odchylenie standardowe” lub „sigma” (od nazwy greckiej litery). Wzór na odchylenie standardowe to:

Aby uzyskać ten wskaźnik dla próbki, użyj wzoru:

Podobnie jak w przypadku wariancji, istnieje nieco inna opcja obliczeń. Ale wraz ze wzrostem próbki różnica znika.
Odchylenie standardowe oczywiście charakteryzuje również miarę rozproszenia danych, ale teraz (w przeciwieństwie do dyspersji) można je porównać z oryginalnymi danymi, ponieważ mają one te same jednostki miary (wynika to jasno ze wzoru obliczeniowego). Ale ten wskaźnik w czystej postaci nie jest zbyt pouczający, ponieważ zawiera zbyt wiele mylących obliczeń pośrednich (odchylenie, kwadrat, suma, średnia, pierwiastek). Niemniej jednak możliwa jest już bezpośrednia praca z odchyleniem standardowym, ponieważ właściwości tego wskaźnika są dobrze zbadane i znane. Na przykład jest to reguła trzech sigma, który stwierdza, że 997 punktów danych na 1000 mieści się w granicach ±3 sigma od średniej arytmetycznej. Odchylenie standardowe, jako miara niepewności, jest również wykorzystywane w wielu obliczeniach statystycznych. Za jego pomocą ustala się stopień dokładności różnych szacunków i prognoz. Jeżeli wariancja będzie bardzo duża, to odchylenie standardowe też będzie duże, w związku z czym prognoza będzie niedokładna, co będzie wyrażone np. w bardzo szerokich przedziałach ufności.
Współczynnik zmienności
Odchylenie standardowe daje bezwzględne oszacowanie miary rozrzutu. Dlatego, aby zrozumieć, jak duży jest spread w stosunku do samych wartości (tj. niezależnie od ich skali), wymagany jest wskaźnik względny. Ten wskaźnik nazywa się Współczynnik zmienności i oblicza się według następującego wzoru:
Współczynnik zmienności jest mierzony w procentach (po pomnożeniu przez 100%). Za pomocą tego wskaźnika można porównywać różne zjawiska, niezależnie od ich skali i jednostek miary. Ten fakt i sprawia, że współczynnik zmienności jest tak popularny.
W statystyce przyjmuje się, że jeśli wartość współczynnika zmienności jest mniejsza niż 33%, to populacja jest uważana za jednorodną, jeśli jest większa niż 33%, to jest heterogeniczna. Trudno mi tu komentować. Nie wiem, kto i dlaczego zdefiniował to w ten sposób, ale jest to uważane za aksjomat.
Czuję, że poniosła mnie sucha teoria i muszę wnieść coś wizualnego i figuratywnego. Z drugiej strony wszystkie wskaźniki zmienności opisują w przybliżeniu to samo, tylko są inaczej obliczane. Dlatego trudno zabłysnąć rozmaitymi przykładami.Różnić się mogą tylko wartości wskaźników, ale nie ich istota. Porównajmy więc, jak różnią się wartości różnych wskaźników zmienności dla tego samego zestawu danych. Weźmy przykład z obliczeniem średniego odchylenia liniowego (z ). Oto oryginalne dane:

I wykres przypominający.

Na podstawie tych danych obliczamy różne wskaźniki wariacje.
Średnia to zwykła średnia arytmetyczna.
Zakres zmienności to różnica między maksimum a minimum:
Średnie odchylenie liniowe oblicza się według wzoru:
Odchylenie standardowe:
Podsumowujemy obliczenia w tabeli.

Jak widać, średnia liniowa i odchylenie standardowe dają podobne wartości stopnia zmienności danych. Wariancja to sigma kwadrat, więc zawsze będzie względna. duża liczba co właściwie nic nie mówi. Zakres zmienności jest różnicą między skrajnościami i może wiele powiedzieć.
Podsumujmy niektóre wyniki.
Zmienność wskaźnika odzwierciedla zmienność procesu lub zjawiska. Jej stopień można zmierzyć za pomocą kilku wskaźników.
1. Zakres zmienności to różnica między maksimum a minimum. zasięg odzwierciedlenia możliwa wartość.
2. Średnie odchylenie liniowe - odzwierciedla średnią bezwzględnych (modulo) odchyleń wszystkich wartości analizowanej populacji od ich wartości średniej.
3. Dyspersja - średni kwadrat odchyleń.
4. Odchylenie standardowe - pierwiastek wariancji (średnie kwadraty odchyleń).
5. Współczynnik zmienności jest najbardziej uniwersalnym wskaźnikiem odzwierciedlającym stopień rozproszenia wartości, niezależnie od ich skali i jednostek miary. Współczynnik zmienności jest mierzony w procentach i może być używany do porównywania zmienności różnych procesów i zjawisk.Tym samym w Analiza statystyczna istnieje system wskaźników odzwierciedlających jednorodność zjawisk i stabilność procesów. Często wskaźniki zmienności nie mają samodzielnego znaczenia i służą do dalszej analizy danych (wyliczanie przedziałów ufności


