Pierwiastek kwadratowy wariancji nazywany jest odchyleniem standardowym od średniej i oblicza się go w następujący sposób:
Podstawowy transformacja algebraiczna Wzór na odchylenie standardowe prowadzi do następującej postaci:
Wzór ten często okazuje się wygodniejszy w praktyce obliczeniowej.
Przeciętny odchylenie standardowe tak samo jak przeciętnie odchylenie liniowe, pokazuje, o ile średnio poszczególne wartości cechy odbiegają od ich wartości średniej. Odchylenie standardowe jest zawsze większe niż średnie odchylenie liniowe. Istnieje między nimi następujący związek:
Znając ten stosunek, możesz na przykład użyć znanych wskaźników do określenia nieznanego, ale (I obliczyć a i odwrotnie. Odchylenie standardowe mierzy bezwzględną wielkość zmienności cechy i wyraża się w tych samych jednostkach miary, co wartości cechy (ruble, tony, lata itp.). Jest to bezwzględna miara zmienności.
Dla znaki alternatywne, na przykład obecność lub nieobecność wyższa edukacja, wzory na ubezpieczenie, dyspersję i odchylenie standardowe przedstawiają się następująco:
Przedstawmy obliczenie odchylenia standardowego na podstawie danych szeregu dyskretnego charakteryzującego rozkład wiekowy studentów jednego z wydziałów uczelni (tabela 6.2).
Tabela 6.2.

Wyniki obliczeń pomocniczych podano w kolumnach 2-5 tabeli. 6.2.
Średni wiek ucznia, w latach, określa się za pomocą wzoru na średnią ważoną arytmetyczną (kolumna 2):
![]()
Kwadraty odchyleń indywidualny wiek ucznia od średniej znajdują się w kolumnach 3-4, a iloczyny kwadratów odchyleń przez odpowiednie częstotliwości znajdują się w kolumnie 5.
Wariancję wieku uczniów, lat, obliczamy korzystając ze wzoru (6.2):
![]()
Wtedy o = l/3,43 1,85 *oda, tj. Każda konkretna wartość wieku ucznia odbiega od średniej o 1,85 roku.
Współczynnik zmienności
W wartości bezwzględnej odchylenie standardowe zależy nie tylko od stopnia zmienności cechy, ale także od bezwzględnych poziomów opcji i średniej. Dlatego nie jest możliwe bezpośrednie porównanie odchyleń standardowych szeregów zmian o różnych poziomach średnich. Aby móc dokonać takiego porównania, trzeba znaleźć środek ciężkościśrednie odchylenie (liniowe lub kwadratowe) średniej arytmetycznej wyrażone w procentach, tj. Oblicz względne miary zmienności.
Liniowy współczynnik zmienności obliczone według wzoru
Współczynnik zmienności wyznaczany za pomocą następującego wzoru:
We współczynnikach zmienności eliminowana jest nie tylko nieporównywalność związana z różnymi jednostkami miary badanej cechy, ale także nieporównywalność powstająca na skutek różnic w wartości średnich arytmetycznych. Ponadto wskaźniki zmienności charakteryzują jednorodność populacji. Populację uważa się za jednorodną, jeśli współczynnik zmienności nie przekracza 33%.
Według tabeli. 6.2 i otrzymane powyżej wyniki obliczeń wyznaczamy współczynnik zmienności %, według wzoru (6.3):
![]()
Jeśli współczynnik zmienności przekracza 33%, oznacza to niejednorodność badanej populacji. Wartość uzyskana w naszym przypadku wskazuje, że populacja uczniów według wieku jest jednorodna pod względem składu. Zatem, ważna funkcja uogólnianie wskaźników zmienności – ocena wiarygodności średnich. Mniej c1, a2 i V, im bardziej jednorodny jest wynikowy zbiór zjawisk i tym bardziej wiarygodna jest otrzymana średnia. Zgodnie z „regułą trzech sigma” stosowaną w statystyce matematycznej, w szeregach o rozkładzie normalnym lub zbliżonych do nich odchylenia od średniej arytmetycznej nieprzekraczające ±3 występują w 997 przypadkach na 1000. Zatem wiedząc X i a, możesz uzyskać ogólne wstępne pojęcie o serii odmian. Jeśli na przykład przeciętne wynagrodzenie pracownika w firmie wynosi 25 000 rubli, a a jest równe 100 rubli, to z prawdopodobieństwem bliskim pewności możemy powiedzieć, że wynagrodzenia pracowników firmy oscylują w przedziale (25 000 ± ± 3 x 100 ) tj. od 24 700 do 25 300 rubli.
Zdefiniowana jako uogólniająca cecha wielkości zmienności cechy w agregacie. Jest on równy pierwiastkowi kwadratowemu średniego kwadratowego odchylenia poszczególnych wartości atrybutu od średniej arytmetycznej, tj. Korzeń i można znaleźć w następujący sposób:
1. Dla wiersza podstawowego:
2. Dla serii zmian:

Transformacja wzoru na odchylenie standardowe sprowadza go do postaci wygodniejszej w praktycznych obliczeniach:
Przeciętny odchylenie standardowe określa, o ile średnio poszczególne opcje odbiegają od ich średniej wartości, jest także bezwzględną miarą zmienności cechy i wyraża się w tych samych jednostkach co opcje, a zatem jest dobrze interpretowany.
Przykłady znajdowania odchylenia standardowego: ,
W przypadku alternatywnych charakterystyk wzór na odchylenie standardowe wygląda następująco:
![]()
gdzie p jest odsetkiem jednostek w populacji, które mają określoną cechę;
q to odsetek jednostek, które nie mają tej cechy.
Pojęcie średniego odchylenia liniowego
Średnie odchylenie liniowe definiuje się jako średnią arytmetyczną wartości bezwzględnych odchyleń poszczególnych opcji od .
1. Dla wiersza podstawowego:

2. Dla serii zmian:

gdzie suma n wynosi suma częstości szeregów zmienności.
Przykład znalezienia średniego odchylenia liniowego:
Zaleta średniego odchylenia bezwzględnego jako miary rozproszenia w zakresie zmienności jest oczywista, ponieważ miara ta polega na uwzględnieniu wszystkich możliwe odchylenia. Ale ten wskaźnik ma znaczące wady. Arbitralne odrzucenie algebraicznych znaków odchyleń może prowadzić do tego, że właściwości matematyczne tego wskaźnika są dalekie od elementarnych. To sprawia, że bardzo trudno jest zastosować średnie odchylenie bezwzględne przy rozwiązywaniu problemów obejmujących obliczenia probabilistyczne.
Dlatego też średnie odchylenie liniowe jako miara zmienności cechy jest rzadko stosowane w praktyce statystycznej, a mianowicie przy sumowaniu wskaźników bez uwzględnienia znaków ma sens ekonomiczny. Za jego pomocą analizowane są na przykład obroty handlu zagranicznego, skład pracowników, rytm produkcji itp.
Średnia kwadratowa
Zastosowano średni kwadrat, na przykład, aby obliczyć średni rozmiar boków n przekrojów kwadratowych, średnie średnice pni, rur itp. Dzieli się na dwa typy.
Prosty średni kwadrat. Jeśli zastępując poszczególne wartości cechy za pomocą Średnia wartość Jeśli konieczne jest utrzymanie stałej sumy kwadratów wartości pierwotnych, wówczas średnia będzie średnią wartością kwadratową.
Jest to pierwiastek kwadratowy z ilorazu sumy kwadratów wartości poszczególnych atrybutów przez ich liczbę:
Średni ważony kwadrat oblicza się ze wzoru:

gdzie f jest znakiem wagi.
Przeciętny sześcienny
Obowiązuje średnia sześcienna na przykład przy określaniu średniej długości boku i sześcianów. Dzieli się na dwa typy.
Średnio sześcienny prosty:


Przy obliczaniu wartości średnich i wariancji w szeregach przedziałowych rozkładów zastępowane są prawdziwe wartości atrybutu wartości centralne przedziały różniące się od średniej arytmetycznej wartości zawartych w przedziale. Prowadzi to do błędu systematycznego przy obliczaniu wariancji. V.F. Sheppard to ustalił błąd w obliczeniu wariancji, spowodowane wykorzystaniem zgrupowanych danych, wynosi 1/12 kwadratu przedziału zarówno w kierunku w górę, jak i w dół wariancji.
Poprawka Shepparda należy stosować, jeśli rozkład jest zbliżony do normalnego, dotyczy cechy o ciągłym charakterze zmienności i opiera się na znacznej ilości danych wyjściowych (n > 500). Jednak biorąc pod uwagę fakt, że w niektórych przypadkach oba błędy, działające w różnych kierunkach, kompensują się wzajemnie, czasami można odmówić wprowadzenia poprawek.
Jak mniejsza wartość wariancji i odchylenia standardowego, tym bardziej jednorodna będzie populacja i tym bardziej typowa będzie średnia.
W praktyce statystycznej często istnieje potrzeba porównywania odmian różne znaki. Na przykład bardzo interesujące jest porównanie różnic w wieku pracowników i ich kwalifikacjach, stażu pracy i wielkości wynagrodzenie, koszty i zyski, staż pracy i wydajność pracy itp. Do takich porównań nie nadają się wskaźniki bezwzględnej zmienności cech: nie można porównać zmienności doświadczenia zawodowego wyrażonej w latach ze zmianą wynagrodzeń wyrażoną w rublach.
Do przeprowadzenia takich porównań, a także porównań zmienności tej samej cechy w kilku populacjach o różnych średnich arytmetycznych, stosuje się względny wskaźnik zmienności - współczynnik zmienności.
Średnie strukturalne
Aby scharakteryzować tendencję centralną w rozkładach statystycznych, często racjonalne jest użycie wraz ze średnią arytmetyczną pewnej wartości cechy X, która ze względu na pewne cechy jej umiejscowienia w szeregu rozkładów może charakteryzować jej poziom.
Jest to szczególnie ważne, gdy w szeregu rozkładu skrajne wartości cechy mają niejasne granice. Z tego powodu precyzyjna definicja Obliczenie średniej arytmetycznej jest zwykle niemożliwe lub bardzo trudne. W takich sprawach średni poziom można określić biorąc na przykład wartość cechy znajdującą się w środku szeregu częstotliwościowego lub występującą najczęściej w bieżącym szeregu.
Wartości takie zależą jedynie od charakteru częstotliwości, czyli od struktury rozkładu. Są one typowe pod względem lokalizacji w szeregu częstotliwości, dlatego takie wartości są uważane za cechy środka rozkładu i dlatego otrzymały definicję średnich strukturalnych. Są przyzwyczajeni do nauki Struktura wewnętrzna oraz strukturę szeregu rozkładu wartości atrybutów. Do takich wskaźników należą:
Odchylenie standardowe to jeden z tych terminów statystycznych w świecie korporacji, który dodaje wiarygodności osobom, którym uda się dobrze je zaprezentować w rozmowie lub prezentacji, pozostawiając jednocześnie niejasne zamieszanie dla tych, którzy nie wiedzą, co to jest, ale są zbyt zawstydzeni, aby zapytać. Tak naprawdę większość menedżerów nie rozumie koncepcji odchylenia standardowego i jeśli jesteś jednym z nich, czas przestać żyć w kłamstwie. W dzisiejszym artykule opowiem Ci, jak ta niedoceniana miara statystyczna może pomóc Ci lepiej zrozumieć dane, z którymi pracujesz.
Co mierzy odchylenie standardowe?
Wyobraź sobie, że jesteś właścicielem dwóch sklepów. Aby uniknąć strat, ważna jest jasna kontrola stanu zapasów. Próbując dowiedzieć się, który menedżer lepiej zarządza zapasami, decydujesz się przeanalizować ostatnie sześć tygodni zapasów. Średni tygodniowy koszt zapasów dla obu sklepów jest w przybliżeniu taki sam i wynosi około 32 jednostek konwencjonalnych. Na pierwszy rzut oka średni odpływ pokazuje, że obaj menedżerowie radzą sobie podobnie.

Ale jeśli przyjrzysz się bliżej działalności drugiego sklepu, przekonasz się, że chociaż średnia wartość jest prawidłowa, zmienność zapasów jest bardzo duża (od 10 do 58 USD). Można zatem stwierdzić, że średnia nie zawsze poprawnie ocenia dane. Tutaj właśnie pojawia się odchylenie standardowe.
Odchylenie standardowe pokazuje, jak wartości rozkładają się w stosunku do średniej w naszym . Innymi słowy, możesz zrozumieć, jak duża jest różnica w odpływie z tygodnia na tydzień.
W naszym przykładzie użyliśmy Funkcja Excela ODCHYLENIE STANDARDOWE, aby obliczyć odchylenie standardowe wraz ze średnią.

W przypadku pierwszego menedżera odchylenie standardowe wyniosło 2. Oznacza to, że każda wartość w próbie odbiega średnio o 2 od średniej. Czy to jest dobre? Spójrzmy na pytanie z innej strony - odchylenie standardowe równe 0 mówi nam, że każda wartość w próbie jest równa jej średniej (w naszym przypadku 32,2). Zatem odchylenie standardowe wynoszące 2 niewiele różni się od 0, co wskazuje, że większość wartości jest bliska średniej. Im odchylenie standardowe jest bliższe 0, tym bardziej wiarygodna jest średnia. Co więcej, odchylenie standardowe bliskie 0 wskazuje na niewielką zmienność danych. Oznacza to, że wartość odpływu z odchyleniem standardowym wynoszącym 2 wskazuje na niesamowitą spójność pierwszego menedżera.
W przypadku drugiego sklepu odchylenie standardowe wyniosło 18,9. Oznacza to, że koszt spływu średnio odbiega o 18,9 od średniej wartości z tygodnia na tydzień. Szalony rozkład! Im odchylenie standardowe jest bardziej od 0, tym mniej dokładna jest średnia. W naszym przypadku liczba 18,9 oznacza, że średniej wartości (32,8 USD tygodniowo) po prostu nie można ufać. Mówi nam to również, że tygodniowy odpływ jest bardzo zmienny.
Tak w skrócie wygląda koncepcja odchylenia standardowego. Chociaż nie zapewnia wglądu w inne ważne pomiary statystyczne (tryb, mediana...), w rzeczywistości odchylenie standardowe odgrywa kluczową rolę w większości obliczeń statystycznych. Zrozumienie zasad odchylenia standardowego rzuci światło na wiele procesów biznesowych.
Jak obliczyć odchylenie standardowe?
Teraz wiemy, co mówi liczba odchylenia standardowego. Zastanówmy się, jak to obliczyć.
Przyjrzyjmy się zbiorowi danych od 10 do 70 w przyrostach co 10. Jak widać, obliczyłem już dla nich wartość odchylenia standardowego za pomocą funkcji STANDARDEV w komórce H2 (na pomarańczowo).

Poniżej znajdują się kroki, jakie wykonuje Excel, aby dotrzeć do wersji 21.6.
Należy pamiętać, że wszystkie obliczenia są wizualizowane w celu lepszego zrozumienia. W rzeczywistości w programie Excel obliczenia odbywają się natychmiast, pozostawiając wszystkie kroki za kulisami.
Najpierw Excel znajduje średnią próbki. W naszym przypadku średnia okazała się wynosić 40, co w kolejnym kroku jest odejmowane od wartości każdej próbki. Każda uzyskana różnica jest podnoszona do kwadratu i sumowana. Otrzymaliśmy sumę równą 2800, którą należy podzielić przez liczbę elementów próbki minus 1. Ponieważ mamy 7 elementów, okazuje się, że musimy podzielić 2800 przez 6. Z wyniku znajdujemy Pierwiastek kwadratowy, liczba ta będzie odchyleniem standardowym.

Dla tych, którzy nie do końca rozumieją zasadę obliczania odchylenia standardowego za pomocą wizualizacji, podaję matematyczną interpretację znalezienia tej wartości.

Funkcje do obliczania odchylenia standardowego w programie Excel
W programie Excel dostępnych jest kilka typów formuł na odchylenie standardowe. Wszystko, co musisz zrobić, to wpisać =STDEV i sam się przekonasz.

Warto zauważyć, że funkcje STDEV.V i STDEV.G (pierwsza i druga funkcja na liście) duplikują odpowiednio funkcje STDEV i STDEV (piąta i szósta funkcja na liście), które zostały zachowane ze względu na zgodność z wcześniejszymi wersje Excela.
Generalnie różnica w zakończeniach funkcji .B i .G wskazuje na zasadę obliczania odchylenia standardowego próbki lub populacja. Wyjaśniłem już różnicę między tymi dwiema tablicami w poprzednim.
Cechą szczególną funkcji STANDARDEV i STANDDREV (trzecia i czwarta funkcja na liście) jest to, że przy obliczaniu odchylenia standardowego tablicy brane są pod uwagę wartości logiczne i tekstowe. Tekst i prawdziwe wartości logiczne to 1, a fałszywe wartości logiczne to 0. Nie wyobrażam sobie sytuacji, w której potrzebowałbym tych dwóch funkcji, więc myślę, że można je zignorować.
X ja - zmienne losowe (bieżące);
X– średnią wartość zmiennych losowych dla próby oblicza się ze wzoru:

Więc, wariancja to średni kwadrat odchyleń . Oznacza to, że najpierw obliczana jest wartość średnia, a następnie pobierana różnica między każdą wartością pierwotną a wartością średnią jest kwadratowa , dodaje się, a następnie dzieli przez liczbę wartości w populacji.
Różnica między wartością indywidualną a średnią odzwierciedla miarę odchylenia. Podnosi się go do kwadratu, aby wszystkie odchylenia stały się wyłącznie liczbami dodatnimi i aby podczas ich sumowania uniknąć wzajemnego niszczenia odchyleń dodatnich i ujemnych. Następnie, biorąc pod uwagę kwadraty odchyleń, po prostu obliczamy średnią arytmetyczną.
Rozwiązanie magiczne słowo„Rozproszenie” składa się właśnie z tych trzech słów: średnia – kwadrat – odchylenia.
Odchylenie standardowe (MSD)
Wyciągając pierwiastek kwadratowy z wariancji, otrzymujemy tzw. odchylenie standardowe". Są nazwiska „odchylenie standardowe” lub „sigma” (od nazwy greckiej litery σ .). Wzór na odchylenie standardowe to:
Więc, dyspersja jest sigma kwadratem lub jest kwadratem odchylenia standardowego.
Odchylenie standardowe, oczywiście, charakteryzuje również miarę rozproszenia danych, ale teraz (w przeciwieństwie do rozproszenia) można ją porównać z danymi pierwotnymi, ponieważ mają one te same jednostki miary (wynika to ze wzoru obliczeniowego). Zakres zmienności to różnica pomiędzy wartościami ekstremalnymi. Odchylenie standardowe, jako miara niepewności, jest również wykorzystywane w wielu obliczeniach statystycznych. Za jego pomocą określa się stopień dokładności różnych szacunków i prognoz. Jeśli wariancja jest bardzo duża, to odchylenie standardowe również będzie duże, a co za tym idzie, prognoza będzie niedokładna, co będzie wyrażone np. w bardzo szerokich przedziałach ufności.
Dlatego w metodach statystycznego przetwarzania danych w wycenach nieruchomości, w zależności od wymaganej dokładności zadania, stosuje się zasadę dwóch lub trzech sigma.
Aby porównać regułę dwóch sigma i regułę trzech sigma, używamy wzoru Laplace’a:
![]() F-F,
F-F,
gdzie Ф(x) jest funkcją Laplace'a;
Minimalna wartość
s = wartość sigma (odchylenie standardowe)
a = średnia
W tym przypadku stosuje się specjalną postać wzoru Laplace’a, gdy granice wartości α i β zmienna losowa X są jednakowo oddalone od środka rozkładu a = M(X) o pewną odległość d: a = a-d, b = a+d.  Lub Lub   (1) Wzór (1) określa prawdopodobieństwo danego odchylenia d zmiennej losowej Xc normalne prawo dystrybucję od niej oczekiwanie matematyczne M(X) = a. Jeśli we wzorze (1) przyjmiemy kolejno d = 2s i d = 3s, otrzymamy: (2), (3). (1) Wzór (1) określa prawdopodobieństwo danego odchylenia d zmiennej losowej Xc normalne prawo dystrybucję od niej oczekiwanie matematyczne M(X) = a. Jeśli we wzorze (1) przyjmiemy kolejno d = 2s i d = 3s, otrzymamy: (2), (3). |
Reguła dwóch sigm
Można niemal wiarygodnie (z prawdopodobieństwem ufności 0,954), że wszystkie wartości zmiennej losowej X z prawem rozkładu normalnego odbiegają od jej oczekiwań matematycznych M(X) = a o kwotę nie większą niż 2s (dwa odchylenia standardowe ). Prawdopodobieństwo ufności (Pd) to prawdopodobieństwo zdarzeń, które są umownie uznawane za wiarygodne (ich prawdopodobieństwo jest bliskie 1).
Zilustrujmy geometrycznie regułę dwóch sigma. Na ryc. Rysunek 6 przedstawia krzywą Gaussa z centrum dystrybucji a. Pole ograniczone całą krzywą i osią Ox jest równe 1 (100%), a pole trapezu krzywoliniowego pomiędzy odciętymi a–2s i a+2s, zgodnie z zasadą dwóch sigma, jest równe do 0,954 (95,4% ogólnej powierzchni). Powierzchnia zacienionych obszarów wynosi 1-0,954 = 0,046 (»5% całkowitej powierzchni). Obszary te nazywane są obszarem krytycznym zmiennej losowej. Wartości zmiennej losowej mieszczące się w obszarze krytycznym są mało prawdopodobne i w praktyce umownie uznawane są za niemożliwe.

Prawdopodobieństwo wartości warunkowo niemożliwych nazywa się poziomem istotności zmiennej losowej. Poziom istotności powiązany jest z prawdopodobieństwem ufności według wzoru:
gdzie q jest poziomem istotności wyrażonym w procentach.
Reguła trzech sigm
Przy rozwiązywaniu problemów wymagających większej niezawodności, gdy przyjmuje się prawdopodobieństwo ufności (Pd) równe 0,997 (dokładniej 0,9973), zamiast reguły dwóch sigma, zgodnie ze wzorem (3), stosuje się regułę trzy sigmy
Według reguła trzech sigm przy prawdopodobieństwie ufności 0,9973 obszarem krytycznym będzie obszar wartości atrybutów poza przedziałem (a-3s, a+3s). Poziom istotności wynosi 0,27%.
Innymi słowy, prawdopodobieństwo, że wartość bezwzględna odchylenia przekroczy trzykrotność odchylenia standardowego, jest bardzo małe i wynosi 0,0027 = 1-0,9973. Oznacza to, że stanie się tak tylko w 0,27% przypadków. Zdarzenia takie, bazując na zasadzie niemożliwości zdarzeń mało prawdopodobnych, można uznać za praktycznie niemożliwe. Te. pobieranie próbek jest bardzo dokładne.
Oto istota reguły trzech sigma:
Jeżeli zmienna losowa ma rozkład normalny, to wartość bezwzględna jej odchylenia od oczekiwań matematycznych nie przekracza trzykrotności odchylenia standardowego (MSD).
W praktyce regułę trzech sigma stosuje się w następujący sposób: jeżeli rozkład badanej zmiennej losowej nie jest znany, ale spełniony jest warunek określony w powyższej regule, to można przypuszczać, że badana zmienna ma rozkład normalny ; w przeciwnym razie nie jest normalnie dystrybuowany.
Poziom istotności jest przyjmowany w zależności od dopuszczalnego stopnia ryzyka i wykonywanego zadania. Do wyceny nieruchomości przyjmuje się zwykle mniej precyzyjną próbę, zgodnie z zasadą dwóch sigma.
$X$. Na początek przypomnijmy następującą definicję:
Definicja 1
Populacja– zbiór losowo wybranych obiektów danego typu, nad którymi prowadzone są obserwacje w celu uzyskania określonych wartości zmiennej losowej, prowadzone w stałych warunkach przy badaniu jednej zmiennej losowej danego typu.
Definicja 2
Ogólna rozbieżność-- przeciętny arytmetyka kwadratów odchylenia wartości wariantu populacji od ich wartości średniej.
Niech wartości opcji $x_1,\ x_2,\dots ,x_k$ mają odpowiednio częstotliwości $n_1,\ n_2,\dots ,n_k$. Następnie wariancję ogólną oblicza się ze wzoru:
Rozważmy szczególny przypadek. Niech wszystkie opcje $x_1,\ x_2,\dots,x_k$ będą różne. W tym przypadku $n_1,\ n_2,\dots,n_k=1$. Stwierdzamy, że w tym przypadku wariancję ogólną obliczamy ze wzoru:
Pojęcie to jest również powiązane z koncepcją ogólnego odchylenia standardowego.
Definicja 3
Ogólne odchylenie standardowe
\[(\sigma)_g=\sqrt(D_g)\]
Odchylenie próbki
Otrzymamy populację próbną w odniesieniu do zmiennej losowej $X$. Na początek przypomnijmy następującą definicję:
Definicja 4
Próbna populacja-- część wybranych obiektów z populacji ogólnej.
Definicja 5
Odchylenie próbki-- średnia arytmetyczna wartości populacji próby.
Niech wartości opcji $x_1,\ x_2,\dots ,x_k$ mają odpowiednio częstotliwości $n_1,\ n_2,\dots ,n_k$. Następnie wariancję próbki oblicza się ze wzoru:
Rozważmy szczególny przypadek. Niech wszystkie opcje $x_1,\ x_2,\dots,x_k$ będą różne. W tym przypadku $n_1,\ n_2,\dots,n_k=1$. Stwierdzamy, że w tym przypadku wariancję próbki oblicza się ze wzoru:
Z tą koncepcją wiąże się również koncepcja odchylenia standardowego próbki.
Definicja 6
Odchylenie standardowe próbki-- pierwiastek kwadratowy z wariancji ogólnej:
\[(\sigma)_в=\sqrt(D_в)\]
Poprawiona wariancja
Aby znaleźć skorygowaną wariancję $S^2$ należy pomnożyć wariancję próbki przez ułamek $\frac(n)(n-1)$, czyli
Pojęcie to jest również powiązane z koncepcją skorygowanego odchylenia standardowego, które oblicza się ze wzoru:
W przypadku, gdy wartości wariantów nie są dyskretne, ale reprezentują przedziały, to we wzorach obliczania wariancji ogólnej lub przykładowej za wartość $x_i$ przyjmuje się wartość środka przedziału do do którego należy $x_i.$.
Przykład problemu znalezienia wariancji i odchylenia standardowego
Przykład 1
Próbną populację definiuje poniższa tabela rozkładu:
Obrazek 1.
Znajdźmy dla niego wariancję próbki, odchylenie standardowe próbki, wariancję skorygowaną i skorygowane odchylenie standardowe.
Aby rozwiązać ten problem, najpierw tworzymy tabelę obliczeniową:
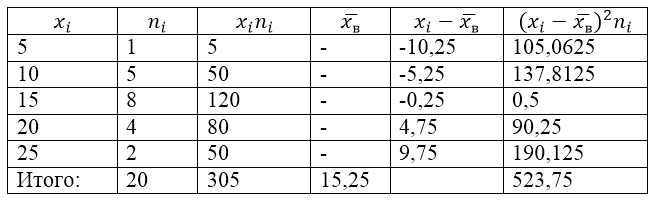
Rysunek 2.
Wartość $\overline(x_в)$ (średnia z próbki) w tabeli wyznacza się ze wzoru:
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15,25\]
Znajdźmy wariancję próbki, korzystając ze wzoru:
Odchylenie standardowe próbki:
\[(\sigma)_в=\sqrt(D_в)\około 5,12\]
Skorygowana wariancja:
\[(S^2=\frac(n)(n-1)D)_в=\frac(20)(19)\cdot 26,1875\około 27,57\]
Skorygowane odchylenie standardowe.


