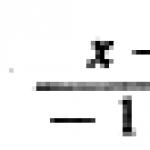Primjer.
Eksperimentalni podaci o varijabilnim vrijednostima h.i w.lED u tablici.
Kao rezultat njihovog poravnanja, dobivena je funkcija ![]()
Upotreba najmanje kvadratna metoda, približno približno ovim podacima linearne ovisnosti y \u003d ax + b (Pronađite parametre ali i b.). Saznajte koja je od dvije linije bolje (u smislu metode najmanjih kvadrata) poravnava eksperimentalne podatke. Napravite crtež.
Suština metode najmanjih kvadrata (MNC).
Zadatak je pronaći koeficijente linearne ovisnosti u kojem funkcija dvije varijable ali i b.
![]() uzima najmanju vrijednost. To jest, s podacima ali i b. Zbroj kvadrata odstupanja eksperimentalnih podataka iz izravne linije bit će najmanji. To je cijela suština metode najmanjih kvadrata.
uzima najmanju vrijednost. To jest, s podacima ali i b. Zbroj kvadrata odstupanja eksperimentalnih podataka iz izravne linije bit će najmanji. To je cijela suština metode najmanjih kvadrata.
Dakle, primjer otopina se svodi na pronalaženje ekstremne funkcije dviju varijabli.
Prikazuje formulu za pronalaženje koeficijenata.
Sustav dviju jednadžbi s dvije nepoznanice je sastavljen i riješen. Nalazimo privatne derivate ![]() varijable ali i b., izjednačiti ove derivate na nulu.
varijable ali i b., izjednačiti ove derivate na nulu. 
Riješiti rezultirajući sustav jednadžbi bilo kojim metodom (na primjer za metodu zamjene ili metoda Cramer) I dobivamo formule za pronalaženje koeficijenata pomoću metode najmanjih kvadrata (MNC). 
S podacima alii b.funkcija ![]() uzima najmanju vrijednost. Dokaz ove činjenice daje se ispod teksta na kraju stranice.
uzima najmanju vrijednost. Dokaz ove činjenice daje se ispod teksta na kraju stranice.
To je cijeli način najmanjih kvadrata. Formula za pronalaženje parametra a. sadrži količine ,, i parametar n. - broj eksperimentalnih podataka. Vrijednosti tih iznosa preporuča se izračunati odvojeno. Koeficijent b. Nalazi se nakon izračuna a..
Vrijeme je da se sjetite o primjeru izvora.
Odluka.
U našem primjeru n \u003d 5., Ispunite tablicu radi lakše izračunavanje količina koje su uključene u formulu željenih koeficijenata. 
Vrijednosti u četvrtom retku tablice dobivaju se množenjem vrijednosti 2. niza na vrijednosti 3. niza za svaki broj i..
Vrijednosti u petom retku tablice dobivene su izgradnjom 2ND vrijednosti za svaki broj. i..
Vrijednosti posljednjeg stupca tablice su iznosa vrijednosti po redovima.
Koristimo formule metode najmanjih kvadrata za pronalaženje koeficijenata ali i b., Zamijenimo odgovarajuće vrijednosti iz zadnjeg stupca tablice: 
Stoga, y \u003d 0.165x + 2.184 - željeni približavajući ravnu liniju.
Ostaje da saznate koja od linija y \u003d 0.165x + 2.184 ili ![]() bolje je približiti početne podatke, to jest, procjenjuje se metodom najmanjih kvadrata.
bolje je približiti početne podatke, to jest, procjenjuje se metodom najmanjih kvadrata.
Procjena pogreške metode najmanjih kvadrata.
To zahtijeva izračunavanje iznosa kvadrata odstupanja izvornih podataka iz tih linija. ![]() i
i ![]() Manja vrijednost odgovara liniji koja je bolja u smislu manji kvadratna metoda približljivima izvorne podatke.
Manja vrijednost odgovara liniji koja je bolja u smislu manji kvadratna metoda približljivima izvorne podatke. 
Jer, onda ravno y \u003d 0.165x + 2.184 Bolje donosi izvorne podatke.
Grafička ilustracija metode najmanjih kvadrata (MNC).
Na grafikonima je sve savršeno vidljivo. Crvena linija je pronađena ravno y \u003d 0.165x + 2.184, Plava linija je ![]() Pink točkice su izvorni podaci.
Pink točkice su izvorni podaci.

U praksi, kada modeliranje različitih procesa - posebno, ekonomske, fizičke, tehničke, socijalne - određene metode za izračunavanje približnih vrijednosti funkcija prema njihovim poznatim vrijednostima u nekim fiksnim mjestima naširoko se koriste.
Ovakav zadatak približavanja funkcija često se događaju:
prilikom konstrukcije približnih formula za izračunavanje vrijednosti karakterističnih vrijednosti proučavanja na tablici dobivenih kao rezultat eksperimenta;
s numeričkom integracijom, diferencijacijom, rješavanjem diferencijalnih jednadžbi, itd.;
ako trebate izračunati vrijednosti funkcija na srednjim točkama razmatranja intervala;
pri određivanju vrijednosti karakterističnih vrijednosti procesa izvan razmatranja u razmatranju, posebno tijekom predviđanja.
Ako simulirati neki proces koji je odredio tablicu, konstruirati funkciju koja približno opisuje ovaj proces na temelju metode najmanjih kvadrata, to će se nazvati približom funkcijom (regresija), a zadatak konstruiranja približnih funkcija je zadatak približavanja sam ,
U ovom se članku raspravlja o mogućnostima MS Excel paketa za rješavanje ove vrste zadataka, dodatno, metode i metode konstruiranja (stvaranja) regresije se daju za tablice navedene funkcije (što je temelj regresijske analize).
U Excelu postoje dvije mogućnosti za izgradnju regresija.
Dodavanje odabranih regresija (trend linije - trendline) na dijagramu na temelju tablice podataka za proučavanje procesa (dostupno samo u prisutnosti izgrađenog dijagrama);
Koristeći ugrađene statističke funkcije radnog lista Excela, omogućujući dobivanje regresije (trend linija) izravno na temelju tablice izvorne podatke.
Dodavanje linija trenda u grafikonu
Za tablicu podataka opisuje neki proces i predstavljen dijagramom, postoji učinkovit regresijski alat u Excelu, koji omogućuje:
graditi na temelju metode najmanjih kvadrata i dodati pet vrsta regresija na dijagram, koji s jednim stupnjem točnosti simulira proces u studiju;
dodajte dijagramu jednadžba konstruirane regresije;
odredite stupanj usklađenosti odabrane regresije prikazane na dijagramu podataka.
Na temelju podataka Excelovog dijagrama omogućuje dobivanje linearni, polinom, logaritamske, snage, eksponencijalne vrste reggestera, koji se daju jednadžba:
y \u003d y (x)
gdje je X neovisna varijabla, koja često uzima vrijednosti slijeda prirodnog raspona brojeva (1; 2; 3; ...) i proizvodi, na primjer, brojeći tijek procesa u studiju (karakteristike ).
1 , Linearna regresija je dobra prilikom modeliranja karakteristika čije se vrijednosti povećavaju ili smanjuju s konstantnom brzinom. To je najjednostavnije u izgradnji procesa u proučavanju. Izgrađena je u skladu s jednadžbom:
y \u003d mx + b
gdje je m tangentni kut sklonosti linearne regresije na Asčissu; B je koordinata na mjestu sjecišta linearne regresije s vlasnikom ordinata.
2 , Polinomi trend je korisna za opisivanje karakteristika koje imaju nekoliko izraženih ekstremnih (maksima i minima). Izbor stupnja polinoma određena je količinom ekstremnih ispitanih karakteristika. Dakle, drugi stupanj polinom može dobro opisati proces sa samo jednim maksimum ili minimum; polinom trećeg stupnja - ne više od dvije krajnosti; Polinoma četvrti stupanj - ne više od tri krajnosti, itd.
U tom slučaju, linija trenda se temelji u skladu s jednadžbom:
y \u003d C0 + C1X + C2X2 + C3X3 + C4X4 + C5X5 + C6X6
tamo gdje koeficijenti C0, C1, C2, ... C6 su konstante, čije se vrijednosti određuju tijekom konstrukcije.
3 , Logaritamska linija trenda uspješno se koristi pri modeliranju karakteristika, koje se vrijednosti prvo mijenjaju brzo, a zatim se postupno stabiliziraju.
y \u003d C ln (X) + b
4 , Linijska linija trenda daje dobre rezultate ako su vrijednosti ovisnosti o ovisnosti karakterizirane konstantnom promjenom stope rasta. Primjer takve ovisnosti može biti graf ravnotežnog kretanja automobila. Ako postoje nula ili negativna vrijednosti među podacima, nemoguće je koristiti trend snage.
Konstruiran u skladu s jednadžbom:
y \u003d c xb
gdje koeficijenti B, C - konstante.
5 , Potrebno je koristiti eksponencijalnu liniju trendova ako se brzina promjene podataka neprestano povećava. Za podatke koji sadrže nulte ili negativne vrijednosti, ova vrsta aproksimacije također nije primjenjiva.
Konstruiran u skladu s jednadžbom:
y \u003d c ebx
gdje koeficijenti B, C - konstante.
Prilikom odabira linije Excel trend automatski izračunava vrijednost vrijednosti R2, koja karakterizira točnost približavanja: bliže vrijednosti R2 na jedan, to je pouzdaniji liniju trenda približava proces u studiju. Ako je potrebno, vrijednost R2 uvijek se može prikazati na dijagramu.
Određeno formulom:

Da biste dodali redak trenda na broj podataka:
aktivirajte dijagram izgrađen na temelju broja podataka, tj. Kliknite na području dijagrama. U glavnom izborniku će se pojaviti paragraf;
nakon što kliknete u ovom trenutku, na zaslonu će se pojaviti izbornik na zaslonu u kojem treba odabrati naredba dodavanja trenda.
Iste akcije su jednostavne za implementaciju ako donesete pokazivač miša na grafikon koji odgovara jednom od serije podataka i desnom tipkom miša; U kontekstnom izborniku koji se pojavi, odaberite liniju za trend. Pojavit će se dijaloški okvir Trend Line s dijaloškom okvirom Otvorenog tipa (Sl. 1).

Nakon toga trebate:
Odaberite vrstu vrste vrste trenda na kartici TIP (odabrana je zadana linearna vrsta). Za tip polinom u polje stupnjeva navedite stupanj odabranog polinom.
1 , Polje izgrađeno na broju navodi sve broj podataka dijagrama koji se razmatraju. Da biste dodali trend liniju na određeni broj podataka, polje je izgrađeno u polju za odabir njegovog imena.

Ako je potrebno, odlaskom na karticu Opcije (Sl. 2), možete postaviti sljedeće parametre za trend line:
promijenite naziv linije trenda u nazivu približno (izglađivana) krivulja.
postavite broj razdoblja (naprijed ili natrag) kako biste predvidjeli polje prognoze;
da biste donijeli jednadžbu trenda na grafikon na grafikon, za ono što bi trebao biti omogućen potvrdni okvir pokazati jednadžbu na dijagramu;
za prikaz vrijednosti točnosti aproksimacije R2 na grafikon, za koji bi trebao biti omogućen da se vrijednost stavi za dijagram, vrijednost točnosti aproksimacije (R ^ 2);
postavite točku raskrižja trenda linije s Y osi, za koju biste trebali omogućiti potvrdni okvir u prelasku krivulje s Y osi na točki;
kliknite gumb U redu da biste zatvorili dijaloški okvir.
Da biste počeli uređivati \u200b\u200bveć izgrađene linije trenda, postoje tri načina:
iskoristite odabranu liniju trenda iz izbornika formata, nakon odabira linije trenda;
odaberite naredbu Format trenda iz kontekstnog izbornika, koji se zove klikom na desno miša duž linije trenda;
dvostruko klikom na liniju trenda.
Dijaloški okvir trend (sl. 3) pojavljuje se na zaslonu, koji sadrži tri kartice: prikaz, vrstu, parametre, a sadržaj posljednje dvije u potpunosti podudara s istim karticama dijaloškog okvira trendova (Sl. 1-2 ). Na kartici Prikaz možete odrediti vrstu linije, njegovu boju i debljinu.

Da biste izbrisali već izgrađen redak trenda, odaberite izbrisanu liniju trenda i pritisnite tipku za brisanje.
Prednosti ispitivane regresijske analize alata su:
relativna jednostavnost izgradnje na dijagrami trenda bez stvaranja podatkovnog tablice za njega;
prilično širok popis vrsta predloženih trend linija, a ovaj popis uključuje najčešće korištene regresijske vrste;
sposobnost predviđanja ponašanja proučavanja u proizvoljnom (unutar zdravog razuma) broj koraka naprijed, kao i natrag;
mogućnost dobivanja jednadžbe linije trenda u analitičkom obliku;
mogućnost, ako je potrebno, dobiti procjenu točnosti provedene aproksimacije.
Sljedeće točke uključuju nedostatke:
izgradnja trenda se provodi samo ako postoji dijagram izgrađen na brojnim podacima;
proces formiranja serije podataka za proučavanu karakteristiku na temelju dobivenih linija za to je donekle zamagljena: željene regresije jednadžbe se ažuriraju sa svakom promjenom vrijednosti izvora retka podataka, ali samo unutar područja dijagrama, Dok se brojni podaci formiraju na temelju trenda starosti stare linije, ostaje nepromijenjen;
u izvješćima konsolidiranih dijagrama prilikom mijenjanja dijagrama ili srodnih izvješća, postojeće trend linije se ne spremaju, to jest, prije održavanja trenda linija ili drugog oblikovanja sažetaka dijagrama, pobrinite se da izgled izvješća zadovoljava potrebne zahtjeve.
Linije trendova uključuju podatke o podacima, prikazani na dijagramima grafikona, histogram, ravne non-normalizirane grafikone s regijama, linijom, točkom, mjehurićom i burzom.
Nemoguće je dopuniti trend linije podataka o rasutom stanju, normaliziranim, laticama, kružnim i prstenskim dijagramima.
Pomoću dodatnih Excelovih funkcija
Excel također ima regresijsku analizu alat za izgradnju trend linija izvan područja dijagrama. U tu svrhu možete koristiti niz statističkih funkcija radnog lista, ali svi nam dopuštaju da izgradimo samo linearne ili eksponencijalne regresije.
Excel ima nekoliko funkcija za izgradnju linearne regresije, osobito:
Nagib i rezati.
TREND;
Kao i nekoliko funkcija za izgradnju eksponencijalne linije trenda, posebno:
LGRFPRIBL.
Treba napomenuti da metode izgradnje regresija koristeći trendove i rast praktički se podudaraju. Isto se može reći o par linena i LGRFPRIBL. Za četiri od tih funkcija, prilikom stvaranja tablice vrijednosti, Excel se koriste kao formule za nizove, što se neznatno popne na proces izgradnje regresije. Također imamo na znanje da je izgradnja linearne regresije, po našem mišljenju, najlakše biti lakše provesti nagib i segment pomoću funkcija, gdje prvi od njih određuje kutni koeficijent linearne regresije, a drugi je segment odrezan po regresiji na ordinatne osi.
Prednosti alata ugrađenih funkcija za regresijsku analizu su:
prilično jednostavna jedinstvena vrsta formacije podataka serije proučavanih karakteristika za sve ugrađene statističke funkcije koje određuju trend linija;
standardna metoda konstruiranja linija trenda na temelju formiranih serija podataka;
sposobnost predviđanja ponašanja procesa u studiju na potreban broj koraka naprijed ili natrag.
A nedostaci uključuju činjenicu da u Excelu nema ugrađenih funkcija za stvaranje drugih (osim linearnih i eksponencijalnih) vrsta trend linija. Ova okolnost često ne dopušta vam da odaberete prilično točan model procesa u studiju, kao i za dobivanje projekcija bliskih stvarnosti. Osim toga, kada koristite funkcije, trend i rast nije poznat na jednadžbi trend linija.
Treba napomenuti da autori nisu postavili svrhu članka da predstave tijek regresijske analize s jednim stupnjem cjelovitosti. Njegov glavni zadatak - na određene primjere, pokazuju značajke Excel paket pri rješavanju približnih zadataka; Pokazati koje učinkovitim alatima za izgradnju regresija i prognoze imaju Excel; Ilustrirajte, kao relativno lako, takve se zadaci mogu riješiti čak i korisnikom koji ne govori duboko poznavanje regresijske analize.
Primjeri rješavanja specifičnih zadataka
Razmotrite rješenje za određene zadatke pomoću nabrojanih alata Excel paketa.
Zadatak 1.
S tablicom podataka o dobiti motornog prijevoza za 1995.-2002. Moraju se izvoditi sljedeće korake.
Izgraditi grafikon.
Dodajte linearni i polinomi (kvadratni i kubični) trend trend na dijagram.
Koristeći jednadžbe linije trenda, za dobivanje tabličnih podataka o dobiti poduzeća za svaku liniju trenda za 1995-2004.
Stvorite prognozu na dobit tvrtke za 2003. i 2004. godinu.
Rješenje problema

U rasponu stanica A4: C11, Excel radionica je uvedena radna tablica prikazana na sl. četiri.
Odvojite raspon stanica B4: C11, gradimo dijagram.
Aktiviramo konstruirani dijagram i prema gore opisanoj metodi nakon odabira vrste trenda u dijaloškom okviru Trend Line (vidi sliku 1) naizmjenično dodajte linearni, kvadratni i kubični trend trend na dijagram. U istom dijaloškom okviru otvorite karticu Parametre (vidi sliku 2), u polju imena približno (izglađivana) krivulja, unesite naziv trenda dodanog i u polju prognoze prema: razdoblja postavljena na 2, Kako se planira napraviti prognozu za dobit za dvije godine unaprijed. Da biste prikazali jednadžbu regresije i valjanosti jednadžbe aproksimacije R2, uključite zastavice kako biste prikazali jednadžbu na zaslonu i stavili dijagram vrijednosti točnosti aproksimacije (R ^ 2). Za bolju vizualnu percepciju mijenjamo vrstu, boju i debljinu izgrađenih trend linija, za koje koristimo karticu Prikaz dijaloškog okvira Format trenda (vidi sliku 3). Dobiveni dijagram s dodatnim linijama trenda prikazana je na Sl. pet.
Za dobivanje tabličnih podataka o dobiti poduzeća za svaku trend liniju za 1995-2004. Koristimo jednadžbe trenda linije prikazane na sl. 5. Da biste to učinili, u rasponu od D3: F3 unosimo tekstualne informacije o vrsti odabrane trend linije: linearnog trenda, kvadratnog trenda, kubičnog trenda. Zatim ulazimo u linearnu regresijsku formulu u ćeliju D4 i, koristeći marker za punjenje, kopirati ovu formulu s relativnim referencama u rasponu stanica D5: D13. Treba napomenuti da svaka ćelija s linearnom regresijskom formulom iz raspona stanica D4: D13 je odgovarajuća stanica iz A4 raspona: A13 kao argument. Slično, za kvadratsku regresiju, raspon stanica E4: E13 je napunjen, a za kubičnu regresiju - raspon stanica F4: F13. Tako je izrađena prognoza na dobit poduzeća za 2003. i 2004. godinu. Uz pomoć tri trendova. Dobivena tablica vrijednosti prikazana je na Sl. 6.


Zadatak 2.
Izgraditi grafikon.
U dijagramu dodaju logaritamske, snage i eksponencijalne trend.
Otpustite jednadžbu dobivenih linija trenda, kao i valjanost aproksimacije R2 za svaku od njih.
Koristeći jednadžbe trend linije, za dobivanje tablica podataka o dobiti tvrtke za svaku liniju trenda za 1995-2002.
Napraviti prognozu za dobit tvrtke za 2003. i 2004. godinu, koristeći ove trend linije.
Rješenje problema
Nakon metode opisane u rješavanju problema, dobivamo dijagram s logaritamskim, snagom i eksponencijalnim trend linijama (sl. 7) dodan u nju (sl. 7). Dalje, korištenjem dobivenih linija trenda, ispunite tablicu vrijednosti poduzeća, uključujući predviđene vrijednosti za 2003. i 2004. godinu. (Sl. 8).


Na sl. 5 i riža. Može se vidjeti da modeli s logaritamskim trendom odgovara najmanjoj vrijednosti točnosti aproksimacije
R2 \u003d 0,8659.
Najveće R2 vrijednosti odgovaraju modelima s polinomnim trendom: kvadratno (R2 \u003d 0.9263) i kubični (R2 \u003d 0.933).
Zadatak 3.
Uz tablicu podataka o dobiti motornog prijevoza poduzeća za 1995.-2002., S obzirom na problem 1, moraju se izvršiti sljedeći koraci.
Nabavite niz podataka za linearni i eksponencijalni trend trend pomoću trenda i rasta funkcija.
Koristeći trend i značajke rasta, napravite prognozu za dobit tvrtke za 2003. i 2004. godinu.
Za izvorne podatke i primljene serije podataka za izgradnju dijagrama.
Rješenje problema
Koristimo radnu tablicu zadataka 1 (vidi sl. 4). Počnimo trend:
odaberite raspon stanica D4: D11, koji bi trebao biti ispunjen vrijednostima funkcije trend koji odgovara poznatim podacima o dobiti poduzeća;
nazovite funkciju naredbe iz izbornika Umetanje. U dijaloškom okviru koji se pojavljuje, čarobnjak za funkciju dodjeljuje funkciju trenda iz statističke kategorije, a zatim kliknite na gumb U redu. Isti rad može se izvesti pritiskom na tipku (Funkcija umetnuti) standardne alatne trake.
U dijaloškom okviru koji se pojavljuje, funkcije argumenti ulaze u polje poznavanje_stacija_y raspon stanica C4: C11; U području poznatih_stations_x - raspon stanica B4: B11;
da bi se dobila formula postala formula polja, koristimo kombinaciju tipki + +.
Formula uvedena od strane SAD-a u nizu će biti: \u003d (trend (C4: C11; B4: B11)).
Kao rezultat toga, raspon stanica D4: D11 je ispunjen odgovarajućim vrijednostima funkcije trenda (sl. 9).

Pripremiti prognozu o dobiti tvrtke za 2003. i 2004. godinu. Potreba:
odaberite raspon stanica D12: D13, gdje će se unijeti vrijednosti predviđene funkcijom trenda.
nazovite funkciju trenda i u dijaloškom okviru argumente koji se pojavljuje, uvodi poznat_y_s_n - raspon stanica C4: C11; U području poznatih_stations_x - raspon stanica B4: B11; Iu polju new_stations_x - raspon stanica B12: B13.
uključite ovu formulu u rješavanju formule pomoću kombinacije tipki Ctrl + Shift +.
Uvedena formula smatrat će se: \u003d (trend (C4: C11; B4: B11; B12: B13)), a raspon stanica D12: D13 će biti napunjen s predviđenim vrijednostima funkcije trend (vidi sl. , 9).
Slično tome, broj podataka je ispunjen funkcijom koja se koristi pri analizi nelinearnih ovisnosti i radi na isti način kao i njegov linearni analogni trend.
Slika 10 prikazuje tablicu u načinu prikaza formula.


Za izvorne podatke i dobivene serije podataka, dijagram prikazani na Sl. jedanaest.
Zadatak 4.
Uz tablicu podataka o prijemu u otpremu usluge motornog prijevoza poduzeća za usluge za razdoblje od 1 do 11, mora se obaviti broj tekućeg mjeseca.
Dobijte seriju podataka za linearnu regresiju: \u200b\u200bkoristeći funkcije nagib i rez; Pomoću linearne funkcije.
Dobijte broj podataka za eksponencijalnu regresiju pomoću funkcije LGRFPRLE.
Koristeći gore navedene funkcije, napravite prognozu za primitak aplikacija u usluge otpreme za razdoblje od 12 do 14 broja tekućeg mjeseca.
Za početne i primljene serije podataka za izgradnju grafikona.
Rješenje problema
Imajte na umu da, za razliku od funkcija, trend i rast, niti jedna od gore navedenih funkcija (nagib, segment, linear, LGRFRIB) nije regresija. Ove funkcije igraju samo pomoćnu ulogu, definiranje potrebnih regresijskih parametara.
Za linearnu i eksponencijalnu regresiju, izgrađena uz pomoć nagiba, segment, linearni, LGRFPRIB, izgled njihovih jednadžbi je uvijek poznat, za razliku od linearnih i eksponencijalnih regresija koji odgovaraju trendu i značajkama rasta.
1 , Konstruiramo linearnu regresiju koja ima jednadžbu:
y \u003d mx + b
koristeći funkcije, nagib i segment, s kutnim regresijskim koeficijentom M, određuje funkciju nagiba, a slobodni član B je funkcija segmenta.
Da biste to učinili, izvršite sljedeće radnje:
uvodimo izvornu tablicu u rasponu stanica A4: B14;
vrijednost MA parametra određuje se u C19 stanici. Odaberite statističku funkciju nagiba iz kategorije; Uvodimo raspon stanica B4: B14 u području poznatih_stations_y i raspon stanica A4: A14 u području poznatih_stations_x. Formula će se uvesti u C19 stanica: \u003d nagib (B4: B14; A4: A14);
s sličnom metodom, parametar vrijednosti B određuje se u D19 stanici. I njegov sadržaj će biti pregledan: \u003d rez (B4: B14; A4: A14). Stoga je potrebno izgraditi linearnu regresiju, parametri M i B će se održavati u skladu s tim u stanicama C19, D19;
zatim ulazimo u C4 staničnu formulu linearne regresije u obliku: \u003d $ c * A4 + $ d. U ovoj formuli, C19 i D19 stanica se bilježi s apsolutnim referencama (adresa stanica ne bi se trebala mijenjati s mogućim kopiranjem). Apsolutni referentni znak može se ispuniti ili s tipkovnice ili pomoću tipke F4, nakon postavljanja pokazivača na adresu stanica. Iskorištavanje markera za punjenje, kopirajte ovu formulu u rasponu C4 stanica: C17. Dobivamo željeni niz podataka (sl. 12). Zbog činjenice da je broj aplikacija cijeli broj, trebali biste postaviti broj prozora staničnog formata numeričkog formata s brojem decimalnih znakova 0.
2 , Sada konstruiramo linearnu regresiju koju daje jednadžba:
y \u003d mx + b
pomoću linearne funkcije.
Za ovo:
ulazimo u funkciju raspona C20: d20 kao linearnu formulu: \u003d (lanena (B4: B14; A4: A4)). Kao rezultat toga, dobivamo u C20 stanici vrijednosti m parametra, au stanici D20 - vrijednost parametra B;
uvodimo u formulu D4 stanice: \u003d $ C * A4 + $ D;
kopirajte ovu formulu pomoću marker za punjenje u rasponu stanica D4: D17 i dobivamo željenu seriju podataka.
3 , Gradimo eksponencijalnu regresiju koja ima jednadžbu:
koristeći funkciju LGRFPRIB, izvodi se na sličan način:
u rasponu stanica C21: D21, ulazimo u funkciju LGRFPRIBL kao formulu polja: \u003d (LGRFPRIBIN (B4: B14; A4: A4: A14)). U ovom slučaju, u C21 stanici, vrijednost m parametar će se odrediti, a u D21 stanici - vrijednost parametra B;
formula se uvodi u E4 ćelija: \u003d $ D * $ C ^ A4;
koristeći marker za punjenje, ova formula se kopira u raspon E4 stanica: E17, gdje će biti brojnih podataka za eksponencijalnu regresiju (vidi sl. 12).

Na sl. Slika 13 prikazuje tablicu na kojoj su vidljive funkcije koje koristimo s potrebnim rasponima stanica, kao i formule.
Vrijednost R. 2 nazvan koeficijent odlučnosti.
Zadatak konstruiranja ovisnosti o regresiji je pronaći vektor koeficijenata M modela (1) u kojem koeficijent r uzima maksimalnu vrijednost.
Da bi se procijenilo značaj r, Fisher's Fischerove f-kriterije koristi se, izračunate formulom

gdje n. - veličina uzorka (broj eksperimenata);
k - broj koeficijenata modela.
Ako F premašuje neku kritičnu vrijednost za podatke n. i k. i usvojila vjerojatnost povjerenja, a vrijednost R smatra se ključnim. Tablice kritičnih vrijednosti F su dani u referentnim knjigama o matematičkoj statistici.
Prema tome, značaj R je određen ne samo zbog njegove vrijednosti, nego i odnosom između količine eksperimenata i broja koeficijenata (parametara) modela. Doista, korelacijski omjer za N \u003d 2 za jednostavan linearni model je 1 (nakon 2 boda u ravnini uvijek se može provesti jedini ravni). Međutim, ako su eksperimentalni podaci slučajnim vrijednostima, vjerujte takvoj vrijednosti R s velikim oprezom. Obično, za dobivanje značajne R i pouzdane regresije, oni nastoje osigurati da broj eksperimenata značajno premašuje broj koeficijenata modela (n\u003e k).
Da biste izgradili linearni regresijski model, potrebno je:
1) Pripremite popis N nizova i MA stupova koji sadrže eksperimentalne podatke (stupac koji sadrži izlaznu vrijednost Yormora biti prvi ili posljednji na popisu); Na primjer, preuzimamo prethodne podatke zadataka dodavanjem stupca s nazivom "Broj perioda", broj broja razdoblja od 1 do 12. (to će biti vrijednosti H.)
2) Kontaktirajte analizu podataka / analize podataka / regresiji

Ako stavku "Analiza podataka" u izborniku "Service" nedostaje, trebate kontaktirati "Add-in" istog izbornika i provjeriti potvrdni okvir "Paket za analizu".
3) U dijaloškom okviru "Regresion":
· Ulazni interval y;
· Ulazni interval X;
· Izlazni interval je gornja lijeva stanica intervala u kojoj će biti postavljeni rezultati izračuna (preporuča se staviti na novi radni list);

4) Pritisnite "OK" i analizirajte rezultate.
- Tutorial
Uvod
Ja sam programer matematičara. Počinio sam najveći skok u moju karijeru kad sam naučio reći: "Ne razumijem ništa!" Sada se ne stidim reći luminaru znanosti, što čita predavanje da ne razumijem što je to, viknuo, kažem mi. I vrlo je teško. Da, teško je priznati u mom neznanju i sramoti. Tko će voljeti priznati da ne zna nešto - tamo. Na temelju vaše profesije moram biti prisutan na velikom broju prezentacija i predavanja, gdje, priznajem, u ogromnoj većini koju želim spavati, jer ne razumijem ništa. I ne razumijem jer veliki problem trenutne situacije u znanosti leži u matematici. Ona sugerira da su svi slušatelji upoznati s apsolutno svim područjima matematike (što je apsurdno). Ispovijedati da ne znate što je derivat (o čemu je malo kasnije) sramota.
Ali naučio sam reći da ne znam što je množenje. Da, ne znam što je subalgebra iznad Algebra Lee. Da, ne znam zašto su kvadratne jednadžbe potrebne u životu. Usput, ako ste sigurni da znate, onda imamo nešto razgovarati! Matematika je niz fokusa. Matematika pokušati zbuniti i zastrašiti javnost; Tamo gdje nema konfuzije, nema reputacije, nema ovlasti. Da, prestižno je govoriti kao apstraktni jezik što je više moguće da postoji potpuna glupost.
Znate li što je izvedeno? Najvjerojatnije mi kažete o granici odnosa razlike. U prvoj godini MatMeach Spbsu Viktor Petrovich me havin određen Derivat kao koeficijent prvog člana taylor niza funkcija u točki (bila je odvojena gimnastika za određivanje taylora serije bez derivata). Dugo sam se nasmijao takvoj definiciji, kao rezultat toga, nisam razumio što je to. Derivat nije ništa drugo nego samo mjera koliko funkcija koju razlikovamo je sličan funkciji y \u003d x, y \u003d x ^ 2, y \u003d x ^ 3.
Sada imam čast da predajemo učenici koji uplašen matematika. Ako se bojite matematike - mi smo s vama na putu. Nakon što pokušavate čitati neki tekst, i čini se vama da je pretjerano komplicirano, onda znate da je napisan. Tvrdim da ne postoji niti jedan prostor matematike, koji se ne može reći "na prstima" bez gubitka točnosti.
Zadatak za blisku budućnost: uputio sam svojim učenicima da shvate što je linearno-kvadratni regulator. Ne oklijevajte, provedite tri minute svog života, idite na link. Ako ne razumijete ništa, onda smo s vama na putu. I (profesionalni matematičar programer) također nije ništa razumio. I uvjeravam ga u ovom može shvatiti "na prstima". U ovom trenutku ne znam što je to, ali uvjeravam da ćemo razumjeti.
Dakle, prvo predavanje ću čitati svoje učenike nakon što su mi užasnice užašuju s riječima da je linearno-kvadratni regulator strašan Bjak, koji nikada ne smije svladati u životu, ovo metode najmanjih kvadrata, Znate li kako riješiti linearne jednadžbe? Ako pročitate ovaj tekst, onda najvjerojatnije ne.
Dakle, dvije točke (X0, Y0), (X1, Y1) su dane, na primjer, (1,1) i (3,2), zadatak da pronađe jednadžbu izravno prolazi kroz ove dvije točke:
ilustracija

Ovo izravno treba imati sljedeću jednadžbu:
Evo nam Alfa i Beta su nam nepoznata, ali dvije točke su poznate po ovom ravnom:
Možete napisati ovu jednadžbu u Matrixovom obliku:
Ovdje je potrebno napraviti lirski povlačenje: što je matrica? Matrica je samo dvodimenzionalni niz. To je način za pohranu podataka, nitko ne bi trebao dati više vrijednosti. To ovisi o nama, kako točno interpretirati matricu. Povremeno ću ga interpretirati kao linearno mapiranje, povremeno kao kvadratni oblik, a ponekad i kao skup vektora. To će se ažurirati u kontekstu.
Zamijenimo određene matrice na njihovom simboličkom prikazu:
Tada se može lako pronaći (alfa, beta):
Konkretnije za naše prethodne podatke:
Što dovodi do sljedeće jednadžbe izravno prolazak kroz točke (1.1) i (3.2):
U redu, sve je jasno ovdje. I pronađimo izravno prolazak jednadžbe tri Bodovi: (X0, Y0), (X1, Y1) i (X2, Y2):
Oh, oh, i imamo tri jednadžbe u dvije nepoznate! Standardni matematičar će reći da rješenja ne postoje. Što će programer reći? I on će prvo prepisati prethodni sustav jednadžbi u sljedećem obliku:
U našem slučaju, vektori I, J, b trodimenzionalni, dakle, (općenito) otopina ovog sustava ne postoji. Bilo koji vektor (Alpha \\ tI + BETA * J) leži u ravnini koja se proteže u vektore (i, J). Ako B ne pripada ovoj ravnini, onda rješenja ne postoje (jednakost u jednadžbi se ne postiže). Što učiniti? Potražimo kompromis. Navedimo kroz e (alfa, beta) Koliko nismo dostigli jednakost:
I pokušat ćemo minimizirati ovu pogrešku:
Zašto trg?
Tražimo ne samo barem normu i barem kvadrat norme. Zašto? Minimalna točka se podudara, a kvadrat daje glatku funkciju (kvadratna funkcija iz agruita (alfa, beta)), dok jednostavno duljina daje funkciju u obliku konusa, nediferencira se na minimalnoj točki. Brr. Kvadrat je prikladniji.
Očito je pogreška minimizirana kada vektor e. ortogonalna ravnina ispružena na vektorima i. i j..
Ilustracija

Drugim riječima: Mi smo u potrazi za tako ravno, da zbroj kvadrata dužine udaljenosti od svih točaka na ovom izravnom je minimalan:
Ažuriranje: Ovdje imam jagnje, udaljenost do ravnometražljivog treba mjeriti okomitom, a ne ortogonalnom projekcijom. Komentar ispravno.
Ilustracija

Bobsmie u različitim riječima (pažljivo, loše formalizirana, ali to bi trebalo biti jasno na prstima): uzimamo sve moguće ravne linije između svih parova bodova i tražeći prosječni izravan između svih:
Ilustracija

Objašnjenje na prstima: Privodimo proljeće između svih točaka podataka (ovdje imamo tri) i usmjeriti da tražimo i izravno ravnotežno stanje je upravo ono što tražimo.
Minimalni kvadratni oblik
Tako da imate ovaj vektor b. i zrakoplov rastegnut na stupcima matričnih vektora A. (U ovom slučaju (X0, X1, X2) i (1,1,1)), tražimo vektor e. S minimalnim kvadratom duljine. Očito, minimum se može ostvariti samo za vektor e., ortogonalna ravnina, ispružena na stupcima-vektorima matrice A.:Drugim riječima, tražimo takav vektor X \u003d (alfa, beta) koji:
Podsjećam vas da je ovaj vektor x \u003d (alfa, beta) minimum kvadratne funkcije || e (alfa, beta) || ^ 2:
Ovdje će biti korisno zapamtiti da se matrica može tumačiti uključujući kao kvadratni oblik, na primjer, jedna matrica ((1.0), (0.1)) može se tumačiti kao funkcija x ^ 2 + y ^ 2:
kvadratni oblik

Sva ta gimnastika poznata su pod imenom linearne regresije.
Laplace jednadžba s graničnim uvjetima Dirichlet
Sada najjednostavniji pravi zadatak: postoji određena triangulirana površina, potrebno ga je izgladiti. Na primjer, učitamo model mog lica:
Na raspolaganju je početno putovanje. Da bih minimizirao vanjske ovisnosti, uzeo sam kod moje softverske renderu, već na Habréu. Da bih riješio linearni sustav, koristim OpenNL, to je izvrstan solver, što je istina, vrlo je teško instalirati: morate kopirati dvije datoteke (.h + .c) u mapu s vašim projektom. Sva izglađivanja se obavlja sljedećim kodom:
Za (int d \u003d 0;<3; d++) {
nlNewContext();
nlSolverParameteri(NL_NB_VARIABLES, verts.size());
nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
nlBegin(NL_SYSTEM);
nlBegin(NL_MATRIX);
for (int i=0; i<(int)verts.size(); i++) {
nlBegin(NL_ROW);
nlCoefficient(i, 1);
nlRightHandSide(verts[i][d]);
nlEnd(NL_ROW);
}
for (unsigned int i=0; i
X, Y i Z koordinate su odvojeni, odvajam ih odvojeno. To jest, rješavam tri sustava linearnih jednadžbi, svaki ima broj varijabli jednakih broju vrhova u mom modelu. Prve N žice matrice A imaju samo jednu jedinicu na nizu, a prvi N redovi vektora B imaju izvorne koordinate modela. To jest, ja se vežem na proljeće između novog položaja vrha i starog položaja vrha - nova ne bi trebala biti daleko od starog.
Sve naknadne linije matrice A (lica.Size () * 3 \u003d količina ruba svih trokuta u mreži) imaju jedan unos 1 i jedan unos To znači da ja druvim proljeće na svakom rubu naše trokutaste mreže: sva rebra pokušavaju dobiti isti vrh kao početnu i konačnu točku.
Još jednom: sve vrhove su varijable i ne mogu daleko od izvorne pozicije, ali pokušavaju postati slični jedni drugima.
Evo rezultata:

Sve je bilo u redu, model je stvarno izglađen, ali se odmaknula od izvornog ruba. Ponovno promijenimo kod:
Za (int i \u003d 0;<(int)verts.size(); i++) { float scale = border[i] ? 1000: 1; nlBegin(NL_ROW); nlCoefficient(i, scale); nlRightHandSide(scale*verts[i][d]); nlEnd(NL_ROW); }
U našoj matrici a, ja sam za vrhove koji su na rubu, dodajte ne niz od pražnjenje v_i \u003d Verts [i], i 1000 * v_i \u003d 1000 * Vrt [i] [i]. Što se mijenja? I to mijenja na naš kvadratni oblik pogreške. Sada je jedno odstupanje od vrha na rubu koštaju ne jednu jedinicu, kao i prije i 1000 * 1000 jedinica. To jest, visjeli smo jačeg proljeća do ekstremnih vrhova, rješenje bi se radije proteželo više. Evo rezultata:

Udvostručimo izvore između vrhova:
nlcoefficient (lice [j], 2); nlcoefficient (lice [(J + 1)% 3], -2);
Logično je da je površina postala glatko:

I sada još sto puta jači:

Što je? Zamislite da smo žičani prsten u sapunici. Kao rezultat toga, rezultirajući sapunski film će pokušati imati najmanju zakrivljenost, koliko je to moguće, dodirujući granice - naše žičane prstenove. To je ono što imamo, popravljajući granicu i tražim da izvučemo glatku površinu. Čestitam vam, upravo smo riješili laplace jednadžbu s graničnim uvjetima Dirishle. Kul zvukovi? Ali u stvari, rješava se samo jedan sustav linearnih jednadžbi.
Poissonova jednadžba
I dalje se sjećamo kul.Pretpostavimo da imam takvu sliku:

Svatko je dobar, samo stolica koju mi \u200b\u200bse ne sviđa.
Mi ćemo smanjiti sliku na pola: 

I on naglašava stolicu: 
Zatim, sve što je bijelo u maski, privlače lijevu stranu slike, a istovremeno ću reći da razlika između dva susjedna piksela treba biti jednaka razlici između dva susjedna piksela s desne slike:
Za (int i \u003d 0; Evo rezultata: Kod i slike dostupni Metoda najmanjih kvadrata (mNA, engleski obični najmanji kvadrati, OLS) - matematička metoda koja se koristi za rješavanje različitih zadataka na temelju minimiziranja zbroja kvadrata odstupanja određenih funkcija iz željenih varijabli. Može se koristiti za "rješavanje" redefiniranih sustava jednadžbi (kada broj jednadžbi premašuje broj nepoznatih), za traženje rješenja u slučaju konvencionalnih (neredirani) nelinearnih sustava jednadžbi, približiti vrijednosti točaka Neke funkcije. MNA je jedna od osnovnih regresijskih analiza metoda za procjenu nepoznatih parametara regresijskih modela na selektivnim podacima. 1
/
5 ✪ metoda najmanjih kvadrata. Predmet ✪ Mitin i.v. - obrada rezultata PIZ. Eksperiment - Metoda najmanjih kvadrata (predavanje 4) ✪ metoda najmanjih kvadrata, lekcija 1/2. Linearna funkcija ✪ ekonometriku. Predavanje 5. Metoda najmanjih kvadrata ✪ metoda najmanjih kvadrata. Odgovoriti Prije početka XIX stoljeća. Znanstvenici nisu imali određena pravila za rješavanje sustava jednadžbi u kojima je broj nepoznatog od broja jednadžbi; Do tog vremena korišteni su privatni prijemi koji su ovisili o vrsti jednadžbi i od oštrine kalkulatora, a time i različita računala na temelju ista opservacijskih podataka došla je do različitih zaključaka. Gaussu (1795) spada u prvu primjenu metode, a Legendre (1805.) samostalno otkriveno i objavljuje ga pod modernim imenom (fra. Méthode des mondres quarris). Laplace je vezao metodu s teorijom vjerojatnosti, a američki matematičar Eldeine (1808.) smatrao je teorijskim i probabilističkim primjenama. Metoda se distribuira i poboljšava daljnja istraživanja ENK, Bessel, Ganzen i drugi. Neka biti X (DisplayStyle X) - Set N (dissystyle n) nepoznate varijable (parametri), f i (x) (dissystyle f_ (i) (x)), , M\u003e n (dissystyle m\u003e n) - skup funkcija iz ovog skupa varijabli. Zadatak je odabrati takve vrijednosti X (DisplayStyle X)tako da su vrijednosti tih funkcija što bliže nekim vrijednostima. Y i (dissystyle y_ (i)), U suštini govorimo o "odluci" redefiniranog sustava jednadžbi f i (x) \u003d y i (dissystyle f_ (i) (x) \u003d y_ (i)), i \u003d 1, ..., m (dissystyle i \u003d 1, ldots, m) U navedenom smislu maksimalne blizine lijevog i desnog dijela sustava. Bit MNA je odabrati kao "Mjere blizine" zbroj kvadrata odstupanja lijevog i desnog dijela | f i (x) - y i | (dissystyle | f_ (i) (x) -y_ (i) |), Dakle, bit MNK može se izraziti na sljedeći način: U slučaju da sustav jednadžbi ima otopinu, onda će barem zbroj kvadrata biti nula i točna rješenja sustava jednadžbi analitički ili, na primjer, različitim numeričkim metodama optimizacije mogu se naći. Ako je sustav nadjačan, to jest, rekavši nevjerojatan, broj neovisnih jednadžbi je veći od broja željenih varijabli, sustav nema točno rješenje, a metoda najmanjih kvadrata omogućuje vam da pronađete neki "optimalni" vektor X (DisplayStyle X) U smislu maksimalne blizine vektora Y (zaslonytyle y) i f (x) (zaslons f (x)) ili maksimalnu blizinu abnormalnog vektora E (zaslon e) Na nulu (blizina se razumije u smislu euklidske udaljenosti). Konkretno, metoda najmanjih kvadrata može se koristiti za "rješavanje" sustava linearnih jednadžbi gdje A (DisplayStyle a) Pravokutna matrica veličine m × n, m\u003e n (DisplayStyle m, n, m\u003e n) (tj. Broj redova matrice A je veći od broja željenih varijabli). Takav sustav jednadžbi u općem slučaju nema rješenja. Stoga se ovaj sustav može "riješiti" samo u smislu izbora takvog vektora X (DisplayStyle X)kako bi se smanjila "udaljenost" između vektora X (zaslonsku sjekiru) i B (displaytyle b), Da biste to učinili, možete primijeniti kriterij za minimiziranje zbroja kvadrata razlike između lijevog i desnog dijelova jednadžbi sustava, to jest (X - b) t (x - b) → min (zaslon (ax-b) ^ (t) (Ax-b) deadarrow men), Lako je pokazati da rješenje ovog minimiziranja dovodi do otopine sljedećeg sustava jednadžbi Neka bude N (dissystyle n) Vrijednosti neke varijable Y (zaslonytyle y) (To mogu biti rezultati opažanja, eksperimenata itd.) I odgovarajuće varijable X (DisplayStyle X), Zadatak je odnos između Y (zaslonytyle y) i X (DisplayStyle X) Približno neke funkcije poznate nekim nepoznatim parametrima B (displaytyle b), to jest, zapravo pronaći najbolje vrijednosti parametara B (displaytyle b)Maksimalne vrijednosti približavanja f (x, b) (Displaytyle f (x, b)) na stvarne vrijednosti Y (zaslonytyle y), Zapravo, to je svedeno na slučaj "rješenja" redefiniranog sustava jednadžbi B (displaytyle b): F (x t, b) \u003d y t, t \u003d 1, ..., n (zaslons f (x_ (t), b) \u003d y_ (t), t \u003d 1, l). U regresijskoj analizi i posebno postoje probabilistički modeli odnosa između varijabli i ekonometriju Y t \u003d f (x t, b) + ε t (zaslonytyle y_ (t) \u003d f (x_ (t), b) + varepsilon _ (t)), gdje ε t (dissystyle varepsilon _ (t)) - takozvano slučajne pogreške Modeli. Prema tome, odstupanja promatranih vrijednosti Y (zaslonytyle y) od modela f (x, b) (Displaytyle f (x, b)) Pretpostavlja se već u samom modelu. Bit MNC (obična, klasična) je pronaći takve parametre B (displaytyle b)na kojoj se zbroj kvadrata devijacija (pogreške za regresijske modele često nazivaju regresijskim ostacima) E t (zaslon e_ (t)) Bit će minimalno: gdje R S (DisplayStyle RSS) - Engleski Rezidualna suma kvadrata definirana je kao: Općenito, rješenje ovog problema može se provesti numeričkim metodama optimizacije (minimiziranje). U ovom slučaju, razgovarajte o tome nelinearni MNC (Nls ili nlls - engleski. Nelinearni najmanje kvadrata). U mnogim slučajevima možete dobiti analitičko rješenje. Da biste riješili problem minimizacije, potrebno je pronaći stacionarne točke funkcije. R s s (b) (zaslon RSS (b))bez navođenja nepoznatih parametara B (displaytyle b), izjednačava derivate na nulu i rješavanje dobivenog sustava jednadžbi: Neka ovisnost o regresiji bude linearna: Neka biti y. - Objašnjenje varijabilnih konopaka, i X (DisplayStyle X) - ovo je (N × K) (dissystyle ((n \\ t, k))))- zadovoljstvo promatranja čimbenika (linije matrice - vektori čimbenika u ovom promatranju, prema stupcima - vektorskim vrijednostima ovog faktora u svim opažanjima). Prikazanost matriksa linearnog modela je: Tada će vektor procjene eksplanatorne varijable i regresijski ostaci biti jednaki prema tome, zbroj kvadrata regresijskih ostataka bit će jednak Razlikovanje ove značajke po vektoru parametara B (displaytyle b) i izjednačiti derivate na nulu, dobivamo sustav jednadžbi (u matričnom obliku): U dešifrirajućem matričnom obliku ovaj sustav jednadžbi je sljedeći: (Σ xt 1 2 σ xt 1 xt 2 xt 1 xt 3 ... Σ xt 1 xtk σ xt 2 xt 1 σ xt 2 2 σ xt 2 xt 3 ... Σ xt 2 xtk σ xt 3 xt 1 xt 3 xt xt 3 2 ... Σ xt 3 xtk ⋮ ⋮ σ σ σ Σ xtkxt 1 Σ xtkxt 2 Σ xtkxt 3 ... Σ XTK 2) (b 1 b 2 b 3 ⋮ bk) \u003d (σ xt 1 yt σ xt 2 yt xt 3 yt ⋮ Σ xtkyt), (zaslon (počnite (pmatrix) suma x_ (t1) ^ (2) suma x_ (t1) x_ (t2) suma x_ (t1) x_ (t3) lDots & sumu X_ (tk) x_ (tk) x_ (t2) x_ (t1) suma x_ (t2) ^ (2) suma x_ (t2) x_ (t3) \\ t ldots & sumi x_ (tk) x_ (t3) x_ (t1) suma x_ (t3) x_ (t2) ^ (2) x_ (t3) ^ (2) i ldots & \\ t Suma x_ (t3) x_ (tk) x_ (t2) x_ (t2) suma x_ (tk) \\ t ) x_ (t3) lDots suma X_ (TK) ^ (2) \\\\\\ cod (pmatrix)) (početi (pmatrix) b_ (1) \\\\\\ B_ (3) \\ t b__ (t) \\\\\\ suma x_ (t2) (t) \\ t t3) y_ (t) \\ t suma x_ (tk) y_ (t) \\ t gdje se svi iznosi uzimaju u svim valjanim vrijednostima T (Displaysyle t). Ako model uključuje konstantu (kao i obično), onda X T 1 \u003d 1 (Displaysyle X_ (T1) \u003d 1) uopće T (Displaysyle t)Stoga je u gornjem lijevom kutu matrice sustava jednadžbi broj opažanja N (dissystyle n)Iu ostalim elementima prve linije i prvog stupca - jednostavno zbroj vrijednosti varijabli: Σ X t j (DisplayStyle Sum X_ (TJ)) i prvi element desnog dijela sustava - Σ y t (Displaysyle sum y_ (t)). Otopinu ovog sustava jednadžbi i daje opću formulu za MN-procjene za linearni model: U analitičke svrhe, potonji zastupljenost ove formule je korisna (u sustavu jednadžbi u dijeljenju n, umjesto da se pojavljuju prosječna aritmetika). Ako je u regresijskom modelu centrniU ovom prezentaciji, prva matrica ima smisla za selektivnu matricu kovarijance čimbenika, a drugi je vektor kovarijance čimbenika s zavisnom varijablom. Ako, osim toga, podaci su također normiran brzinom (to je, u konačnici standardiziran), onda prva matrica ima značenje selektivne matrice korelacije čimbenika, drugi vektor - vektor selektivnih korelacija čimbenika s zavisnom varijablom. Važno vlasništvo MN-procjena za modele s Constanta - Linija izgrađenu regresiju prolazi kroz središte gravitacije uzoraka podataka, odnosno se izvodi jednakost: Konkretno, kao posljednje utočište, kada je jedini regresor konstantna, dobivamo da je MNC-evaluacija jednog parametra (zapravo konstantna) jednaka prosječnoj vrijednosti varijable koja se može objašnjava. To jest, aritmetički prosjek, poznat po svojim dobrim nekretninama iz zakona velikih brojeva, također je procjena MNK - zadovoljava kriterij najmanje zbroja kvadrata odstupanja od nje. U slučaju uparene linearne regresije y t \u003d a + b x t + ε t t (zaslonyyle y_ (t) \u003d a + bx_ (t) + varepsilon _ (t))Kada se procjenjuje linearna ovisnost jedne varijable od drugog, izračun formule su pojednostavljeni (bez matrične algebre). Sustav jednadžbi je: Odavde je lako pronaći ocjene koeficijenata: Unatoč činjenici da je u općem slučaju modela s konstantnim poželjnim, u nekim slučajevima, poznato je iz teorijskih razmatranja koja konstantna A (DisplayStyle a) mora biti nula. Na primjer, u fizici, ovisnost između napona i struje ima oblik U \u003d i ⋅ r (dissystyle u \u003d i cDot r); Mjerna napetost i struja struja, potrebno je procijeniti otpor. U ovom slučaju govorimo o modelu Y \u003d B x (Displaysyle Y \u003d BX), U tom slučaju, umjesto sustava jednadžbi imamo jedinu jednadžbu (Σ x t 2) b \u003d σ x t y t (dissystyle lijevo (suma x_ (t) ^ (2) desno) b \u003d suma x_ (t) y_ (t)). Prema tome, formula za procjenu jedinog koeficijenta ima oblik B ^ \u003d σ t \u003d 1 nxttyt σ t \u003d 1 nxt 2 \u003d xy ¯ x 2 ¯ (consystsyle (šešir (b)) \u003d (frac (sumi _ (t \u003d 1) ^ (n) x_ (t) x_ (t ) y_ (t)) (suma _ (t \u003d 1) ^ (n) x_ (t) ^ (2))) \u003d (frac (grafika (xy)) (prekogranični (x ^ (2)) ))))))))). Ako su podaci aproksimirani funkcijom polinomalne regresije jedne varijable f (x) \u003d b 0 + σ i \u003d 1 k b i x i (x) \u003d b_ (0) + suma granice _ (i \u003d 1) ^ (k) b_ (i) x ^ (i) x ^ (i)), percipiranje stupnjeva X I (DisplayStyle X ^ (i)) kao neovisni čimbenici za svaki I (dissystyle i) Možete procijeniti parametre modela na temelju opće formule za procjenu parametara linearnog modela. Za to je opća formula dovoljna da se to razmotri s takvim tumačenjem x t i x t j \u003d x t i x t j \u003d x t i + j (TJ) x_ (TJ) \u003d x_ (t) ^ (i) x_ (t) ^ (j) \u003d x_ (t) ^ (i + j)) i x t j y t \u003d x t j y t (DisplayStyle x_ (tj) y_ (t) \u003d x_ (t) ^ (j) y_ (t)), Zbog toga će matrične jednadžbe u ovom slučaju pogledati: (n Σ nxt ... Σ nxk Σ nxi 2 ... Σ mxik + 1 ⋮ σ σ σ Σ nxk Σ nxk + 1 ... Σ nxt 2 k) [b 0 b 1 ⋮ bk] \u003d [σ nyt Σ nxtyt ⋮ Σ nxkyt]. (DisplayStyle (početi (pmatrix) n sumu granice _ (n) x_ (t) _ (n) x_ (t) _ (n) x_ (t) ^ (k) granice _ ( n) x_ (t) suma granice _ (n) x_ (i) ^ (2) ldots suma granica _ (m) x_ (i) ^ (k + 1). \\ T VDots & \\ t DDots \\ _ (n) X_ (t) ^ (k) suma granice _ (n) x_ (t) ^ (k + 1) ldots & sumu granice _ (n) x_ (t) ^ (2k) kraj (pmatrix)) (početi (bmatrix) b_ (0) \\\\ b_ (1) \\\\ VDots \\\\\\ B_ (B) END (BMATRIX)) \u003d (početi granice _ (n) y_ (t) granice _ (n) x_ (t) y_ (t) \\\\\\ vDots \\ t (n) x_ (n) x_ (t) x_ (t) x_ (t ) ^ (k) y_ (t) kraj (bmatrix)).) Prije svega, napominjemo da su za linearni modeli procjene MNA linearne procjene, kako slijedi iz gornje formule. Za invaliditet MNK-procjena, potrebno je i dovoljno ispunjenje najvažnijih uvjeta za regresijsku analizu: uvjetni faktorima matematičko očekivanje na slučajnu pogrešku trebala bi biti nula. Ovo stanje, posebno se izvodi ako Drugi uvjet je stanje egzogenih čimbenika - glavnica. Ako je to nekretnina nije ispunjena, može se pretpostaviti da će gotovo bilo kakve procjene biti iznimno nezadovoljavajuće: neću biti ni pravne (to jest, čak i vrlo velika količina podataka ne dopušta da se dobiju kvalitativne procjene u ovom slučaju). U klasičnom slučaju, napravljena je snažnija pretpostavka određivanja čimbenika, za razliku od slučajne pogreške, koja automatski znači ispunjenje uvjeta izgaranja. Općenito, za dosljednost procjena, dovoljno je izvršiti uvjet o izlučivanju zajedno s konvergencijom matrice V x (DisplayStyle v_ (x)) Na neke ne-degenerirane matrice s povećanjem veličine uzorka do beskonačnosti. Osim dosljednosti i nesposobnosti, procjene (uobičajeno), MNC su također učinkoviti (najbolji u klasi linearnih nestalnih procjena) zahtijeva dodatna svojstva slučajne pogreške: Te se pretpostavke mogu formulirati za matricu kovarijance slučajnih pogrešaka. V (ε) \u003d σ 2 i (Displaytyle v (varepsilon) \u003d sigma ^ (2) i). Pozvan je linearni model koji zadovoljava takve uvjete klasičan, MNA procjene za klasičnu linearnu regresiju su nestabilne, weissial i najučinkovitije procjene u razredu svih linearnih nepovezanih procjena (na engleskom jeziku literature ponekad se koristi od strane kratice Plavo (Najbolji linearni nepristrani procjenitelj) - najbolja linearna nedvosmislena procjena; U domaćoj književnosti češće se daje Gaussova - Markova teoma). Kako je lako pokazati, kovarijantna matrica izgledi koeficijenata bit će jednaka: V (b ^ ols) \u003d σ 2 (xtx) - 1 (Displaytyle v ((šešir (b)) _ (ols)) \u003d sigma ^ (2) (x ^ (t) x) ^ (- 1 )))). Učinkovitost znači da je ova kovarijanca matrica "minimalna" (bilo koja linearna kombinacija koeficijenata, a posebno koeficijenti sami, imaju minimalnu disperziju), odnosno u klasi linearnih nevjerojatnih procjena MNK-najbolje procjene. Dijagonalni elementi ove matrice - Disperzija procjena koeficijenata važni su parametri kvalitete procjena. Međutim, nemoguće je izračunati matricu kovarijance, budući da je disperzija slučajnih pogrešaka nepoznata. Može se dokazati da je neograničeno i bogato (za klasični linearni model) procjene disperzije slučajnih pogrešaka vrijednost: S 2 \u003d R S / (n - K) (Displayyle S ^ (2) \u003d RSS / (n - K)). Zamjena te vrijednosti u formuli za matricu kovarijance i dobije procjenu matrice kovarijance. Dobivene procjene također su nestabilne i bogate. Također je važno da disperzija pogreške evaluacije (i stoga disperzije koeficijenata) i procjene parametara modela su neovisne slučajne vrijednosti, što vam omogućuje da dobijete ispitne statistike za testiranje hipoteza o koeficijentima modela. Treba napomenuti da ako se ne ispune klasične pretpostavke, procjene MNK-a o parametrima nisu najučinkovitije i, gdje W (dissystyle w) - Neke simetrične pozitivno definirane matrice težine. Normalni MNC je poseban slučaj ovog pristupa, kada je matrica težine proporcionalna jednom matrici. Kao što je poznato, postoji razgradnja za simetrične matrice (ili operatore) W \u003d p t p (displaytyle w \u003d p ^ (t) p), Stoga se navedena funkcionalnost može predstavljati kako slijedi. e t tptp e \u003d (p e) tp e \u003d e * t e * (t) p ^ (t) P ^ (t) PE \u003d (PE) ^ (t) pe \u003d e_ (*) \u200b\u200b^ (t) e_ ( *)))To jest, ova funkcionalnost može biti predstavljena kao zbroj kvadrata nekih od transformiranih "ostataka". Dakle, možete odabrati klasu najmanjih kvadrata metode - metode (najmanje kvadrati). Dokazano je (teorem AITKEK), koji je za generalizirani linearni regresijski model (u kojem se ne nameću ograničenja na matricu kovarijanske matrice slučajnih pogrešaka) su najučinkovitije (u klasi linearnih nepovezanih procjena) procjene T.N. generalizirani MNC (OmNA, GLS - Generalizirani najmanje kvadrati) - LS-Metode s matricom na težini jednaka obrnutom kovarijanskoj matrici slučajnih pogrešaka: W \u003d v ε - 1 (dissystyle w \u003d v _ (varepsilon) ^ (- 1)). Može se pokazati da formula za procjene OMNA-a parametara linearnog modela ima oblik B ^ gls \u003d (xtv - 1 x) - 1 xtv - 1 y (zaslon (šešir (b)) _ (GLS) \u003d (x ^ (t) v ^ (- 1) x) ^ (- 1) X ^ (t) v ^ (- 1) y). Kovarijanac matrica ovih procjena će biti jednaka V (b ^ gls) \u003d (xtv - 1 x) - 1 (Displaytyle v ((šešir (b)) _ (GLS)) \u003d (x ^ (t) v ^ (- 1) x) ^ (- jedan)). Zapravo, suština OMNA je specifična (linearna) transformacija (P) izvornih podataka i korištenje običnih MNC na transformirane podatke. Svrha ove transformacije je za pretvaranje podataka slučajnih pogrešaka već zadovoljavaju klasične pretpostavke. U slučaju matrice dijagonalne težine (i stoga kovarijantne matrice slučajnih pogrešaka) imamo takozvani ponderirani mNA (wls - ponderirani najmanji kvadrati). U tom slučaju, ponderirana zbroj kvadrata ostataka modela je minimizirana, tj. Svako promatranje dobiva "težinu", obrnuto proporcionalnu disperziju slučajne pogreške u ovom promatranju: E tw e \u003d σ t \u003d 1 neto 2 σ t 2 (dissystyle e ^ (t) we \u003d sumi _ (t \u003d 1) ^ (n) (frac (e_ (t) ^ (2)) (\\ t Sigma _ (t) ^ (2))))), U stvari, podaci se pretvaraju promatranje vaganja (podjela po veličini proporcionalnom proporcionalnom standardnom devijaciji slučajnih pogrešaka), a obično se primjenjuje uobičajeni MNC na suspendirane podatke. ISBN 978-5-7749-0473-0. Najmanje kvadratna metoda Najmanje kvadratna metoda ( MNA, ols, obični najmanji kvadrati)
- Jedna od osnovnih metoda regresijske analize za procjenu nepoznatih parametara regresijskih modela na uzorcima podataka. Metoda se temelji na minimiziranju zbroja kvadrata regresijskih ostataka. Treba napomenuti da se način rješavanja problema u bilo kojem području može pozvati na bilo koji način, ako odluka leži ili zadovoljava neki kriterij za minimiziranje zbroja kvadrata nekih funkcija iz željenih varijabli. Stoga se metoda najmanjih kvadrata može koristiti i za približnu reprezentaciju (aproksimacija) određene funkcije od strane drugih (jednostavnijih) funkcija, dok pronalazite skup vrijednosti koje zadovoljavaju jednadžbe ili ograničenja, čiji broj prelazi Broj tih vrijednosti itd. Neka određeni (parametarski) model probabilističkih (regresijski) ovisnosti između (objašnjenih) varijable y. i više čimbenika (objašnjenje varijabli) x. gdje - Vektor nepoznati model parametri Pretpostavimo da i postoje selektivna opažanja vrijednosti navedenih varijabli. Neka - broj promatranja (). Zatim - vrijednosti varijabli u -m promatranje. Zatim, pri specificiranim vrijednostima parametara B, možete izračunati teorijske (modelne) vrijednosti objašnjenja varijable Y: Vrijednost ostataka ovisi o vrijednostima parametara b. Suština MNC-a (konvencionalna, klasična) je pronaći takve parametre B, na kojem zbroj kvadrata ostataka (Eng. Rezidualna zbroj kvadrata ) Bit će minimalno: Općenito, rješenje ovog problema može se provesti numeričkim metodama optimizacije (minimiziranje). U ovom slučaju, razgovarajte o tome nelinearni MNC (Nls ili nlls - engleski. Nelinearni najmanji kvadrati). U mnogim slučajevima možete dobiti analitičko rješenje. Kako bi se riješio problem minimizacije, potrebno je pronaći stacionarne točke funkcije usmjeravanjem prema nepoznatim parametrima B, izjednačenim derivatima na nulu i rješavanje dobivenog sustava jednadžbi: Ako pogreška slučajnih modela imaju normalnu raspodjelu, imaju istu disperziju i nekorelaciju, procjene MNK-a o parametrima se podudaraju s procjenama maksimalne metode istinitosti (MMP). Neka ovisnost o regresiji bude linearna: Neka biti y. - promatranje eksploatatorne varijable, a - matrica promatranja čimbenika (linija matrica - vektora vrijednosti čimbenika u ovom promatranju, prema stupcima - vektorskim vrijednostima ovog faktora u svim opažanjima) , Prikazanost matriksa linearnog modela je: Tada će vektor procjene eksplanatorne varijable i regresijski ostaci biti jednaki prema tome, zbroj kvadrata regresijskih ostataka bit će jednak Razlikovanje ove značajke pomoću vektora parametara i izjednačenih derivata na nulu, dobivamo sustav jednadžbi (u matričnom obliku): Otopinu ovog sustava jednadžbi i daje opću formulu za MN-procjene za linearni model: Za analitičke svrhe, posljednja zastupljenost ove formule je korisna. Ako je u regresijskom modelu centrniU ovom prezentaciji, prva matrica ima smisla za selektivnu matricu kovarijance čimbenika, a drugi je vektor kovarijance čimbenika s zavisnom varijablom. Ako, osim toga, podaci su također normiran brzinom (to je, u konačnici standardiziran), onda prva matrica ima značenje selektivne matrice korelacije čimbenika, drugi vektor - vektor selektivnih korelacija čimbenika s zavisnom varijablom. Važno vlasništvo MN-procjena za modele s Constanta - Linija izgrađenu regresiju prolazi kroz središte gravitacije uzoraka podataka, odnosno se izvodi jednakost: Konkretno, kao posljednje utočište, kada je jedini regresor konstantna, dobivamo da je MNC-evaluacija jednog parametra (zapravo konstantna) jednaka prosječnoj vrijednosti varijable koja se može objašnjava. To jest, aritmetički prosjek, poznat po svojim dobrim nekretninama iz zakona velikih brojeva, također je procjena MNK - zadovoljava kriterij najmanje zbroja kvadrata odstupanja od nje. U slučaju uparene linearne regresije, izračun formula je pojednostavljena (bez matrice algebra): Prije svega, napominjemo da su za linearni modeli procjene MNA linearne procjene, kako slijedi iz gornje formule. Za invaliditet MNK-procjena, potrebno je i dovoljno ispunjenje najvažnijih uvjeta za regresijsku analizu: uvjetni faktorima matematičko očekivanje na slučajnu pogrešku trebala bi biti nula. Ovo stanje, posebno se izvodi ako Drugi uvjet je stanje egzogenih čimbenika - glavnica. Ako je to nekretnina nije ispunjena, može se pretpostaviti da će gotovo bilo kakve procjene biti iznimno nezadovoljavajuće: neću biti ni pravne (to jest, čak i vrlo velika količina podataka ne dopušta da se dobiju kvalitativne procjene u ovom slučaju). U klasičnom slučaju, napravljena je snažnija pretpostavka određivanja čimbenika, za razliku od slučajne pogreške, koja automatski znači ispunjenje uvjeta izgaranja. Općenito, za dosljednost procjena, dovoljno je obaviti uvjet o izlučivanju zajedno s konvergencijom matrice na određenu ne-degenerivnu matricu s povećanjem veličine uzorka do beskonačnosti. Osim dosljednosti i nesposobnosti, procjene (uobičajeno), MNC su također učinkoviti (najbolji u klasi linearnih nestalnih procjena) zahtijeva dodatna svojstva slučajne pogreške: Te se pretpostavke mogu formulirati za matricu kovarijance slučajnih pogrešaka. Pozvan je linearni model koji zadovoljava takve uvjete klasičan, MNA procjene za klasičnu linearnu regresiju su nestabilne, weissial i najučinkovitije procjene u razredu svih linearnih nepovezanih procjena (na engleskom jeziku literature ponekad se koristi od strane kratice Plavo (Najbolji linearni propalični procjenitelj) - najbolja linearna nedvosmislena procjena; U domaćoj književnosti češće se daje Gaussova - Markova teoma). Kako je lako pokazati, kovarijantna matrica izgledi koeficijenata bit će jednaka: Metoda najmanjih kvadrata omogućuje široku generalizaciju. Umjesto minimiziranja zbroja kvadrata ostataka, možete minimizirati neki pozitivno definirani kvadratni oblik iz preostalog vektora, gdje - neke simetrične pozitivno definirane matrice težine. Normalni MNC je poseban slučaj ovog pristupa, kada je matrica težine proporcionalna jednom matrici. Kao što je poznato iz teorije simetričnih matrica (ili operatora) za takve matrice postoji raspadanje. Stoga se navedena funkcionalnost može predstavljati kako slijedi, to jest, ova funkcionalnost može biti predstavljena kao zbroj kvadrata nekih pretvorenih "ostataka". Dakle, možete odabrati klasu najmanjih kvadrata metode - metode (najmanje kvadrati). Dokazano je (teorem AITKEK), koji je za generalizirani linearni regresijski model (u kojem se ne nameću ograničenja na matricu kovarijanske matrice slučajnih pogrešaka) su najučinkovitije (u klasi linearnih nepovezanih procjena) procjene T.N. generalizirani MNC (OmNA, GLS - Generalizirani najmanje kvadrati) - LS-Metode s matricom na težini jednaka obrnutom kovarijanskoj matrici slučajnih pogrešaka :. Može se pokazati da formula za procjene OMNA-a parametara linearnog modela ima oblik Kovarijanac matrica ovih procjena će biti jednaka Zapravo, suština OMNA je specifična (linearna) transformacija (P) izvornih podataka i korištenje običnih MNC na transformirane podatke. Svrha ove transformacije je za pretvaranje podataka slučajnih pogrešaka već zadovoljavaju klasične pretpostavke. U slučaju matrice dijagonalne težine (i stoga kovarijantne matrice slučajnih pogrešaka) imamo takozvani ponderirani mNA (wls - ponderirani najmanji kvadrati). U tom slučaju, ponderirana zbroj kvadrata ostataka modela je minimizirana, tj. Svako promatranje dobiva "težinu", obrnuto proporcionalnu disperziju slučajne pogreške u ovom promatranju :. U stvari, podaci se pretvaraju promatranje vaganja (podjela po veličini proporcionalnom proporcionalnom standardnom devijaciji slučajnih pogrešaka), a obično se primjenjuje uobičajeni MNC na suspendirane podatke. Razmotriti slučaj kada je rezultat proučavanja ovisnosti neke skalarne vrijednosti od neke skalarne vrijednosti (to može biti, na primjer, ovisnost napona od trenutne sile:, gdje - konstantna vrijednost, otpor vodiča) mjerena je ovim vrijednostima, kao rezultat toga dobivene vrijednosti i odgovarajuće vrijednosti. Mjerni podaci moraju biti zabilježeni u tablici. Stol. Rezultati mjerenja. Pitanje zvuči ovako: Koja je vrijednost koeficijenta da se odlučite najbolje opisati ovisnost? Prema MN-u, ta vrijednost bi trebala biti takva da zbroj kvadrata odstupanja od vrijednosti bilo je minimalno Zbroj kvadrata odstupanja ima jedan ekstrem - minimum, što nam omogućuje da koristimo ovu formulu. Pronađite iz ove formule vrijednost koeficijenta. Da bismo to učinili, preobrazimo njegov lijevi dio kako slijedi: Potonja formula omogućuje nam da pronađemo vrijednost koeficijenta, koja je bila potrebna u zadatku. Prije početka XIX stoljeća. Znanstvenici nisu imali određena pravila za rješavanje sustava jednadžbi u kojima je broj nepoznatog od broja jednadžbi; Do tog vremena korišteni su privatni prijemi koji su ovisili o vrsti jednadžbi i od oštrine kalkulatora, a time i različita računala na temelju ista opservacijskih podataka došla je do različitih zaključaka. Gaussu (1795) spada u prvu primjenu metode, a Legendre (1805.) samostalno otkriveno i objavljuje ga pod modernim imenom (fra. Méthode des mondres quarris
). Laplace je vezao metodu s teorijom vjerojatnosti, a američki matematičar Eldeine (1808.) smatrao je teorijskim i probabilističkim primjenama. Metoda se distribuira i poboljšava daljnja istraživanja ENK, Bessel, Ganzen i drugi. Ideja metode najmanjih kvadrata također se može koristiti u drugim slučajevima koji nisu izravno povezani s regresijskom analizom. Činjenica je da je zbroj kvadrata jedna od najčešćih blizina vektora (eurlidska metrika u konačnim - dimenzionalnim prostorima). Jedna od aplikacija je "rješenje" sustava linearnih jednadžbi, u kojima je broj jednadžbi veći od broja varijabli gdje matrica nije kvadratna, ali pravokutna veličina. Takav sustav jednadžbi, općenito nema rješenja (ako je rang zapravo više od broja varijabli). Stoga se ovaj sustav može "riješiti" samo u smislu odabira takav vektor kako bi se smanjila "udaljenost" između vektora i. Da biste to učinili, možete primijeniti kriterij za minimiziranje zbroja kvadrata razlike između lijevog i desnog dijelova jednadžbi sustava, odnosno. Lako je pokazati da rješenje ovog minimiziranja dovodi do otopine sljedećeg sustava jednadžbi Metoda najmanjih kvadrata je matematički postupak za pripravu linearne jednadžbe, najviše odgovarajući setu naručenog pare, pronalaženjem vrijednosti za A i B, koeficijenti u ravnoj jednadžbi. Svrha metode najmanjih kvadrata je minimiziranje ukupne kvadratne pogreške između vrijednosti Y i ŷ. Ako za svaku točku određujemo pogrešku ŷ, metoda najmanjih kvadrata smanjuje: gdje je n \u003d broj naručenih parova oko linije. Maksimalne relevantne podatke. Ovaj koncept je ilustriran na slici. Sudeći po slici, liniju, maksimalni odgovarajući podaci, regresijska linija, minimizira ukupnu kvadratnu pogrešku od četiri točke na grafikonu. Pokazat ću vam kako to odrediti pomoću manjih kvadratnih metoda na sljedećem primjeru. Zamislite mladi par, koji, nedavno, živjeti zajedno i dijeliti stol za kozmetički pribor u kupaonici. Mladić je počeo primijetiti da je polovica svog stola neumoljivo opada dijelu njihovih pozicija za kosu i sojine komplekse. Tijekom proteklih nekoliko mjeseci, tip je pažljivo slijedio, po kojoj brzini se povećava broj stavki na njemu. Tablica u nastavku prikazuje broj objekata djevojčica na stolu u kupaonici, akumuliran u posljednjih nekoliko mjeseci. Budući da smo definirali zadatak pronalaženja, hoće li se broj objekata, "mjesec" povećati s vremenom, a "broj objekata" ovisi. Koristeći metodu najmanjih kvadrata, određujemo jednadžbu koja je maksimum koji odgovara podacima izračunavanjem vrijednosti A, segment na Y osi i B, linije linije: a \u003d y cf - bx cp gdje je X CP prosječna vrijednost X, neovisna varijabla, y cf - prosječna vrijednost Y, neovisna varijabla. Tablica u nastavku sažima izračun potreban za te jednadžbe. Krivulja učinka za naš primjer s kupaonicom određuje se sljedećom jednadžbom: Budući da naša jednadžba ima pozitivan nagib - 0,976, tip ima dokaze da se broj stavki na stolu tijekom vremena povećava prosječnu brzinu 1 subjekta mjesečno. Grafikon prikazuje krivulju učinka s naručenim parovima. Čekanje na broj objekata u sljedećoj polovici godine (16 mjeseci) izračunat će se kako slijedi: ŷ \u003d 5.13 + 0.976x \u003d 5.13 + 0.976 (16) ~ 20.7 \u003d 21 Dakle, vrijeme je da naš junak poduzme bilo kakve radnje. Kao što ste već vjerojatno pogodili u Excelu postoji funkcija za izračunavanje vrijednosti način najmanjih kvadrata.Ova se značajka naziva trend. Sintaksa je sljedeća: Trend (poznate vrijednosti y; poznate X vrijednosti; nova X vrijednosti; const) poznate vrijednosti Y - niz zavisnih varijabli, u našem slučaju, broj objekata na stolu poznate vrijednosti X - niz neovisnih varijabli, u našem slučaju to je mjesec dana nove X vrijednosti - Nove X (mjesečno) vrijednosti za koje funkcija trenda Vraća očekivanu vrijednost ovisnih varijabli (broj stavki) const - opcionalno. Logička vrijednost koja označava je li konstanta B jednaka 0. Na primjer, slika prikazuje funkcijski trend koji se koristi za određivanje očekivanog broja objekata na stolu u kupaonici 16. mjeseca.
Enciklopedic youtube.
Titlovi
Povijest
Suština metode najmanjih kvadrata
Primjer - Sustav linearnih jednadžbi
MNG u regresijskoj analizi (približavanje podataka)
MNA u slučaju linearne regresije
Najjednostavniji posebni slučajevi
Slučaj polinomalnog modela
Statistička svojstva procjena MNK
Ponderirani MNC
Suština MNC-a
MNA u slučaju linearnog modela
Primjer: najjednostavniji (par) regresija
Svojstva procjena MNK
Generalizirani MNK.
Ponderirani MNC
Neki posebni slučajevi primjene MNA u praksi
Aproksimacija linearne ovisnosti
Mjerni broj
1
2
3
4
5
6
Povijest
Alternativna uporaba MNK.







Trend funkcije u Excelu