The inverse matrix for a given one is such a matrix, multiplication of the original one by which gives the identity matrix: A mandatory and sufficient condition for the presence inverse matrix is the inequality zero of the determinant of the original (which in turn implies that the matrix must be square). If the determinant of a matrix is equal to zero, then it is called degenerate and such a matrix has no inverse. In higher mathematics, inverse matrices are important and are used to solve a number of problems. For example, on finding the inverse matrix a matrix method for solving systems of equations is constructed. Our service site allows calculate inverse matrix online two methods: the Gauss-Jordan method and using the matrix of algebraic additions. The first one implies a large number of elementary transformations inside the matrix, the second - the calculation of the determinant and algebraic additions to all elements. To calculate the determinant of a matrix online, you can use our other service - Calculating the determinant of a matrix online
.Find the inverse matrix on the site
website allows you to find inverse matrix online fast and free. On the site, calculations are made by our service and a result is displayed with a detailed solution for finding inverse matrix. The server always gives only the exact and correct answer. In tasks by definition inverse matrix online, it is necessary that the determinant matrices was different from zero, otherwise website will report the impossibility of finding the inverse matrix due to the fact that the determinant of the original matrix is equal to zero. Finding task inverse matrix found in many branches of mathematics, being one of the most basic concepts of algebra and a mathematical tool in applied problems. Independent inverse matrix definition requires considerable effort, a lot of time, calculations and great care in order not to make a slip or a small error in the calculations. Therefore, our service finding the inverse matrix online will greatly facilitate your task and will become an indispensable tool for solving mathematical problems. Even if you find inverse matrix yourself, we recommend checking your solution on our server. Enter your original matrix on our Calculate Inverse Matrix Online and check your answer. Our system is never wrong and finds inverse matrix given dimension in the mode online instantly! On the site website character entries are allowed in elements matrices, in this case inverse matrix online will be presented in general symbolic form.
The matrix $A^(-1)$ is called the inverse of the square matrix $A$ if $A^(-1)\cdot A=A\cdot A^(-1)=E$, where $E $ is the identity matrix, the order of which is equal to the order of the matrix $A$.
A non-singular matrix is a matrix whose determinant is not equal to zero. Accordingly, a degenerate matrix is one whose determinant is equal to zero.
The inverse matrix $A^(-1)$ exists if and only if the matrix $A$ is nonsingular. If the inverse matrix $A^(-1)$ exists, then it is unique.
There are several ways to find the inverse of a matrix, and we'll look at two of them. This page will cover the adjoint matrix method, which is considered standard in most courses. higher mathematics. The second way to find the inverse matrix (method of elementary transformations), which involves the use of the Gauss method or the Gauss-Jordan method, is considered in the second part.
Adjoint (union) matrix method
Let the matrix $A_(n\times n)$ be given. In order to find the inverse matrix $A^(-1)$, three steps are required:
- Find the determinant of the matrix $A$ and make sure that $\Delta A\neq 0$, i.e. that the matrix A is nondegenerate.
- Compose algebraic complements $A_(ij)$ of each element of the matrix $A$ and write down the matrix $A_(n\times n)^(*)=\left(A_(ij) \right)$ from the found algebraic complements.
- Write the inverse matrix taking into account the formula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.
The matrix $(A^(*))^T$ is often referred to as the adjoint (mutual, allied) matrix of $A$.
If the decision is made manually, then the first method is good only for matrices of relatively small orders: second (), third (), fourth (). To find the inverse of a matrix higher order, other methods are used. For example, the Gauss method, which is discussed in the second part.
Example #1
Find matrix inverse to matrix $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.
Since all elements of the fourth column are equal to zero, then $\Delta A=0$ (i.e. the matrix $A$ is degenerate). Since $\Delta A=0$, there is no matrix inverse to $A$.
Example #2
Find the matrix inverse to the matrix $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$.
We use the adjoint matrix method. First, let's find the determinant of the given matrix $A$:
$$ \Delta A=\left| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$
Since $\Delta A \neq 0$, then the inverse matrix exists, so we continue the solution. Finding Algebraic Complements
\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(aligned)
Compose a matrix of algebraic complements: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.
Transpose the resulting matrix: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (the resulting matrix is often is called the adjoint or union matrix to the matrix $A$). Using the formula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, we have:
$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$
So the inverse matrix is found: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $. To check the truth of the result, it is enough to check the truth of one of the equalities: $A^(-1)\cdot A=E$ or $A\cdot A^(-1)=E$. Let's check the equality $A^(-1)\cdot A=E$. In order to work less with fractions, we will substitute the matrix $A^(-1)$ not in the form $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$ but as $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array )\right)$:
Answer: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.
Example #3
Find the inverse of the matrix $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$.
Let's start by calculating the determinant of the matrix $A$. So, the determinant of the matrix $A$ is:
$$ \Delta A=\left| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36+56-12=26. $$
Since $\Delta A\neq 0$, then the inverse matrix exists, so we continue the solution. We find the algebraic complements of each element of the given matrix:

We compose a matrix of algebraic additions and transpose it:
$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) $$
Using the formula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, we get:
$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$
So $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 & -3/26 & 37/26 \end(array) \right)$. To check the truth of the result, it is enough to check the truth of one of the equalities: $A^(-1)\cdot A=E$ or $A\cdot A^(-1)=E$. Let's check the equality $A\cdot A^(-1)=E$. In order to work less with fractions, we will substitute the matrix $A^(-1)$ not in the form $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, but as $\frac(1)(26)\cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:
The check was passed successfully, the inverse matrix $A^(-1)$ was found correctly.
Answer: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.
Example #4
Find matrix inverse of $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.
For a matrix of the fourth order, finding the inverse matrix using algebraic additions is somewhat difficult. However, such examples control work meet.
To find the inverse matrix, first you need to calculate the determinant of the matrix $A$. The best way to do this in this situation is to expand the determinant in a row (column). We select any row or column and find the algebraic complement of each element of the selected row or column.
Finding the inverse matrix- a problem that is most often solved by two methods:
- the method of algebraic additions, in which it is required to find determinants and transpose matrices;
- the Gaussian elimination method, which requires elementary transformations of matrices (add rows, multiply rows by the same number, etc.).
For those who are especially curious, there are other methods, for example, the method of linear transformations. In this lesson, we will analyze the three methods mentioned and algorithms for finding the inverse matrix by these methods.
inverse matrix BUT, such a matrix is called
BUT
. (1)
inverse matrix , which is required to be found for a given square matrix BUT, such a matrix is called
the product by which the matrices BUT on the right is the identity matrix, i.e.,
. (1)
An identity matrix is a diagonal matrix in which all diagonal entries are equal to one.
Theorem.For each non-singular (non-singular, non-singular) square matrix, one can find an inverse matrix, and moreover, only one. For a special (degenerate, singular) square matrix, the inverse matrix does not exist.
The square matrix is called non-special(or non-degenerate, non-singular) if its determinant is not equal to zero, and special(or degenerate, singular) if its determinant is zero.
The inverse matrix can only be found for a square matrix. Naturally, the inverse matrix will also be square and of the same order as the given matrix. A matrix for which an inverse matrix can be found is called an invertible matrix.
For inverse matrix there is an apt analogy with the reciprocal of a number. For every number a, which is not equal to zero, there exists a number b that the work a and b equal to one: ab= 1 . Number b is called the reciprocal of a number b. For example, for the number 7, the inverse is the number 1/7, since 7*1/7=1.
Finding the inverse matrix by the method of algebraic additions (union matrix)
For a non-singular square matrix BUT the inverse is the matrix
where is the matrix determinant BUT, а is the matrix associated with the matrix BUT.
Allied with a square matrix A is a matrix of the same order whose elements are the algebraic complements of the corresponding elements of the determinant of the matrix transposed with respect to the matrix A. Thus, if

then 
and 
Algorithm for finding the inverse matrix by the method of algebraic additions
1. Find the determinant of this matrix A. If the determinant is equal to zero, finding the inverse matrix stops, since the matrix is degenerate and there is no inverse for it.
2. Find a matrix transposed with respect to A.
3. Calculate the elements of the union matrix as the algebraic complements of the marita found in step 2.
4. Apply formula (2): multiply the reciprocal of the determinant of the matrix A, to the union matrix found in step 4.
5. Check the result obtained in step 4 by multiplying this matrix A to the inverse matrix. If the product of these matrices is equal to the identity matrix, then the inverse matrix was found correctly. Otherwise start the solution process again.
Example 1 For matrix
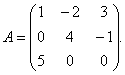
find the inverse matrix.
Solution. To find the inverse matrix, it is necessary to find the determinant of the matrix BUT. We find by the rule of triangles:

Therefore, the matrix BUT is non-singular (non-degenerate, non-singular) and there is an inverse for it.
Let's find the matrix associated with the given matrix BUT.
Let's find the matrix transposed with respect to the matrix A:
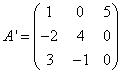
We calculate the elements of the union matrix as algebraic complements of the matrix transposed with respect to the matrix A:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, the matrix conjugated with the matrix A, has the form
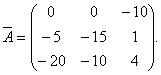
Comment. The order of calculation of elements and transposition of the matrix may be different. One can first compute the algebraic complements of the matrix A, and then transpose the matrix of algebraic complements. The result should be the same elements of the union matrix.
Applying formula (2), we find the matrix inverse to the matrix BUT:

Finding the Inverse Matrix by Gaussian Elimination of Unknowns
The first step to find the inverse matrix by Gaussian elimination is to assign to the matrix A identity matrix of the same order, separating them with a vertical bar. We get a dual matrix. Multiply both parts of this matrix by , then we get
![]() ,
,
Algorithm for finding the inverse matrix by the Gaussian elimination of unknowns
1. To the matrix A assign an identity matrix of the same order.
2. Transform the resulting dual matrix so that the identity matrix is obtained in its left part, then the inverse matrix will automatically be obtained in the right part in place of the identity matrix. Matrix A on the left side is converted to the identity matrix by elementary transformations of the matrix.
2. If in the process of matrix transformation A into the identity matrix in any row or in any column there will be only zeros, then the determinant of the matrix is equal to zero, and, therefore, the matrix A will be degenerate, and it has no inverse matrix. In this case, further finding of the inverse matrix stops.
Example 2 For matrix
find the inverse matrix.
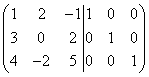
and we will transform it so that the identity matrix is obtained on the left side. Let's start the transformation.
Multiply the first row of the left and right matrix by (-3) and add it to the second row, and then multiply the first row by (-4) and add it to the third row, then we get
 .
.
So that, if possible, there are no fractional numbers during subsequent transformations, we will first create a unit in the second row on the left side of the dual matrix. To do this, multiply the second row by 2 and subtract the third row from it, then we get
 .
.
Let's add the first row to the second, and then multiply the second row by (-9) and add it to the third row. Then we get
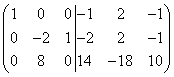 .
.
Divide the third row by 8, then
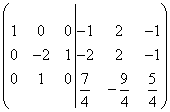 .
.
Multiply the third row by 2 and add it to the second row. It turns out:
 .
.
Swapping the places of the second and third lines, then we finally get:
 .
.
We see that the identity matrix is obtained on the left side, therefore, the inverse matrix is obtained on the right side. In this way:
 .
.
You can check the correctness of the calculations by multiplying the original matrix by the found inverse matrix:
The result should be an inverse matrix.
Example 3 For matrix
find the inverse matrix.
Solution. Compiling a dual matrix

and we will transform it.
We multiply the first row by 3, and the second by 2, and subtract from the second, and then we multiply the first row by 5, and the third by 2 and subtract from the third row, then we get
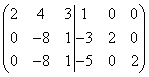 .
.
We multiply the first row by 2 and add it to the second, and then subtract the second from the third row, then we get
 .
.
We see that in the third line on the left side, all elements turned out to be equal to zero. Therefore, the matrix is degenerate and has no inverse matrix. We stop further finding of the reverse maria.
Let there be a square matrix of the nth order
Matrix A -1 is called inverse matrix with respect to the matrix A, if A * A -1 = E, where E is the identity matrix of the nth order.
Identity matrix- such a square matrix, in which all elements along the main diagonal, passing from the upper left corner to the lower right corner, are ones, and the rest are zeros, for example:
inverse matrix may exist only for square matrices those. for those matrices that have the same number of rows and columns.
Inverse Matrix Existence Condition Theorem
For a matrix to have an inverse matrix, it is necessary and sufficient that it be nondegenerate.
The matrix A = (A1, A2,...A n) is called non-degenerate if the column vectors are linearly independent. The number of linearly independent column vectors of a matrix is called the rank of the matrix. Therefore, we can say that in order for an inverse matrix to exist, it is necessary and sufficient that the rank of the matrix is equal to its dimension, i.e. r = n.
Algorithm for finding the inverse matrix
- Write the matrix A in the table for solving systems of equations by the Gauss method and on the right (in place of the right parts of the equations) assign matrix E to it.
- Using Jordan transformations, bring matrix A to a matrix consisting of single columns; in this case, it is necessary to simultaneously transform the matrix E.
- If necessary, rearrange the rows (equations) of the last table so that the identity matrix E is obtained under the matrix A of the original table.
- Write the inverse matrix A -1, which is in the last table under the matrix E of the original table.
For matrix A, find the inverse matrix A -1

Solution: We write down the matrix A and on the right we assign the identity matrix E. Using the Jordan transformations, we reduce the matrix A to the identity matrix E. The calculations are shown in Table 31.1.

Let's check the correctness of the calculations by multiplying the original matrix A and the inverse matrix A -1.

As a result of matrix multiplication, the identity matrix is obtained. Therefore, the calculations are correct.
Answer: 
Solution of matrix equations
Matrix equations can look like:
AX = B, XA = B, AXB = C,
where A, B, C are given matrices, X is the desired matrix.
Matrix equations are solved by multiplying the equation by inverse matrices.
For example, to find the matrix from an equation, you need to multiply this equation by on the left.
Therefore, to find a solution to the equation, you need to find the inverse matrix and multiply it by the matrix on the right side of the equation.
Other equations are solved similarly.

Solve the equation AX = B if 
Solution: Since the inverse of the matrix equals (see example 1)
Matrix method in economic analysis
Along with others, they also find application matrix methods. These methods are based on linear and vector-matrix algebra. Such methods are used for the purposes of analyzing complex and multidimensional economic phenomena. Most often, these methods are used when it is necessary to compare the functioning of organizations and their structural divisions.
In the process of applying matrix methods of analysis, several stages can be distinguished.
At the first stage system is being formed economic indicators and on its basis, a matrix of initial data is compiled, which is a table in which system numbers are shown in its individual lines (i = 1,2,....,n), and along the vertical graphs - numbers of indicators (j = 1,2,....,m).
At the second stage for each vertical column, the largest of the available values of the indicators is revealed, which is taken as a unit.
After that, all the amounts reflected in this column are divided by highest value and a matrix of standardized coefficients is formed.
At the third stage all components of the matrix are squared. If they have different significance, then each indicator of the matrix is assigned a certain weighting coefficient k. The value of the latter is determined by an expert.
On the last fourth stage found values of ratings Rj grouped in order of increasing or decreasing.
The above matrix methods should be used, for example, in a comparative analysis of various investment projects, as well as in assessing other economic performance indicators of organizations.



