In this article, we will take a comprehensive look at . Basic trigonometric identities are equalities that establish a relationship between the sine, cosine, tangent and cotangent of one angle, and allow you to find any of these trigonometric functions through a known other.
We immediately list the main trigonometric identities, which we will analyze in this article. We write them down in a table, and below we give the derivation of these formulas and give the necessary explanations.
Page navigation.
Relationship between sine and cosine of one angle
Sometimes they talk not about the main trigonometric identities listed in the table above, but about one single basic trigonometric identity kind ![]() . The explanation for this fact is quite simple: the equalities are obtained from the basic trigonometric identity after dividing both of its parts by and respectively, and the equalities
. The explanation for this fact is quite simple: the equalities are obtained from the basic trigonometric identity after dividing both of its parts by and respectively, and the equalities  and
and ![]() follow from the definitions of sine, cosine, tangent, and cotangent. We will discuss this in more detail in the following paragraphs.
follow from the definitions of sine, cosine, tangent, and cotangent. We will discuss this in more detail in the following paragraphs.
That is, it is the equality that is of particular interest, which was given the name of the main trigonometric identity.
Before proving the basic trigonometric identity, we give its formulation: the sum of the squares of the sine and cosine of one angle is identically equal to one. Now let's prove it.
The basic trigonometric identity is very often used in transformation of trigonometric expressions. It allows the sum of the squares of the sine and cosine of one angle to be replaced by one. No less often, the basic trigonometric identity is used in reverse order: the unit is replaced by the sum of the squares of the sine and cosine of any angle.
Tangent and cotangent through sine and cosine
Identities connecting the tangent and cotangent with the sine and cosine of one angle of the form and ![]() immediately follow from the definitions of sine, cosine, tangent and cotangent. Indeed, by definition, the sine is the ordinate of y, the cosine is the abscissa of x, the tangent is the ratio of the ordinate to the abscissa, that is,
immediately follow from the definitions of sine, cosine, tangent and cotangent. Indeed, by definition, the sine is the ordinate of y, the cosine is the abscissa of x, the tangent is the ratio of the ordinate to the abscissa, that is, ![]() , and the cotangent is the ratio of the abscissa to the ordinate, that is,
, and the cotangent is the ratio of the abscissa to the ordinate, that is, ![]() .
.
Due to this obviousness of the identities and ![]() often the definitions of tangent and cotangent are given not through the ratio of the abscissa and the ordinate, but through the ratio of the sine and cosine. So the tangent of an angle is the ratio of the sine to the cosine of this angle, and the cotangent is the ratio of the cosine to the sine.
often the definitions of tangent and cotangent are given not through the ratio of the abscissa and the ordinate, but through the ratio of the sine and cosine. So the tangent of an angle is the ratio of the sine to the cosine of this angle, and the cotangent is the ratio of the cosine to the sine.
To conclude this section, it should be noted that the identities and ![]() hold for all such angles for which the trigonometric functions in them make sense. So the formula is valid for any other than (otherwise the denominator will be zero, and we did not define division by zero), and the formula
hold for all such angles for which the trigonometric functions in them make sense. So the formula is valid for any other than (otherwise the denominator will be zero, and we did not define division by zero), and the formula ![]() - for all , different from , where z is any .
- for all , different from , where z is any .
Relationship between tangent and cotangent
An even more obvious trigonometric identity than the previous two is the identity connecting the tangent and cotangent of one angle of the form ![]() . It is clear that it takes place for any angles other than , otherwise either the tangent or the cotangent is not defined.
. It is clear that it takes place for any angles other than , otherwise either the tangent or the cotangent is not defined.
Proof of the formula ![]() very simple. By definition and from where
very simple. By definition and from where  . The proof could have been carried out in a slightly different way. Since and
. The proof could have been carried out in a slightly different way. Since and ![]() , then
, then  .
.
So, the tangent and cotangent of one angle, at which they make sense, is.
Topic: Trigonometric formulas (25 hours)
Lesson 6 - 7: Relationship between sine, cosine and tangent of the same angle.
Target: study the relationship between the sine, cosine and tangent of the same angle. To achieve this goal it is necessary:
- Know:
- formulations of definitions of the main trigonometric functions (sine, cosine and tangent); signs of trigonometric functions in quarters; set of values of trigonometric functions; basic formulas of trigonometry.
- Understand:
- that the basic trigonometric identity can only be used for one and the same argument; algorithm for calculating one trigonometric function through another.
- Apply:
- the ability to choose the right formula for solving a specific task; ability to work with simple fractions; the ability to perform the transformation of trigonometric expressions.
- Analysis:
- analyze errors in the logic of reasoning.
- Synthesis:
- offer your own way of solving examples; make a crossword puzzle using the knowledge gained.
- Grade:
- knowledge and skills on this topic for use in other sections of algebra.
- Organizing time.
- Updating knowledge and skills.
- In what quarter is an angle of 1 radian and what is it approximately equal to?
- What word is missing in the definition of the sine function?
- What word is missing in the definition of the cosine function?
- What values can a sine take?
 ()
() - Explanation of new material.
 let us draw a unit circle centered at the point O. Let the radius OB be obtained by turning the radius OA, equal to R, through the angle (Fig. 5). Then by definition
let us draw a unit circle centered at the point O. Let the radius OB be obtained by turning the radius OA, equal to R, through the angle (Fig. 5). Then by definition 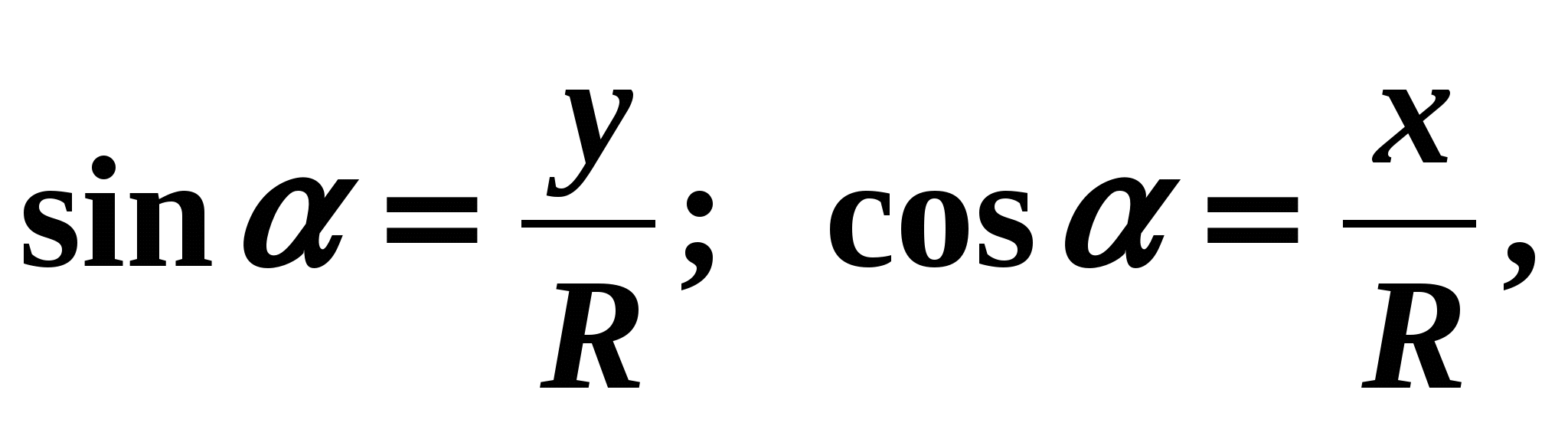 where
where  - abscissa of point B,
- abscissa of point B, 
 is its ordinate. It follows that Point B belongs to the circle. Therefore, its coordinates satisfy the equation
is its ordinate. It follows that Point B belongs to the circle. Therefore, its coordinates satisfy the equation 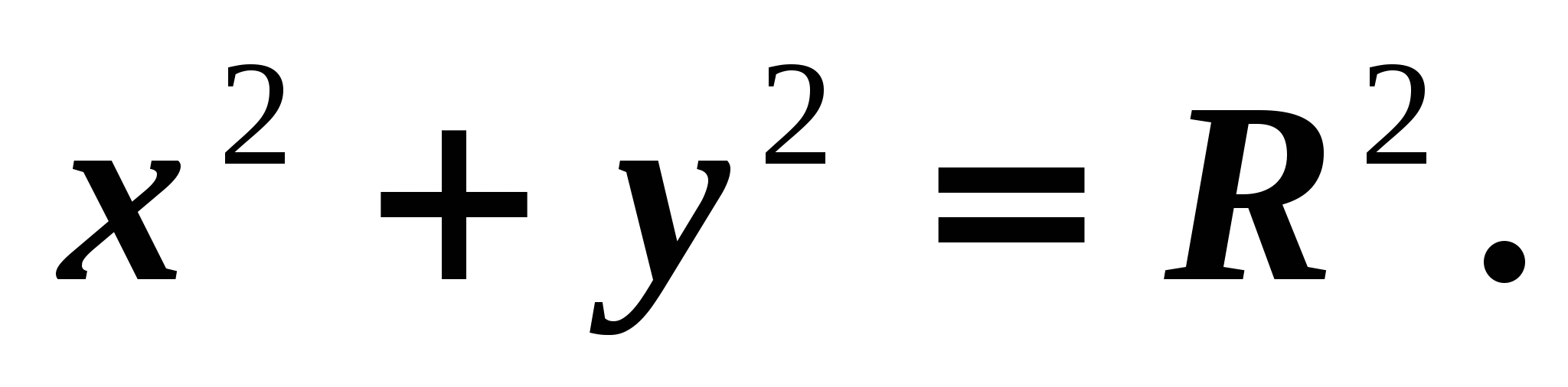 Using what we get
Using what we get  (1).
We have obtained an equality that is valid for any values of the letters included in it. What are these equalities called? That's right - identities. Equality (1) is called basic trigonometric identity. In equality (1) can take any values. Complete the recording yourself:
(1).
We have obtained an equality that is valid for any values of the letters included in it. What are these equalities called? That's right - identities. Equality (1) is called basic trigonometric identity. In equality (1) can take any values. Complete the recording yourself: 1.
Check if your entry is correct. Put yourself points in the lesson card for Tasks number 2. We continue. We have derived the basic trigonometric identity, but why do we need it? That's right - to find the cosine value from one known value of the sine and vice versa. Now we can always use the basic trigonometric identity, but the main thing is for the same argument. Students in the notebook are invited to independently express from the basic trigonometric identity the sine through the cosine and the cosine through the sine. Two students are called to the board to check. One is invited to express the sine through the cosine, the second - the cosine through the sine. The correct answer is displayed on the screen:
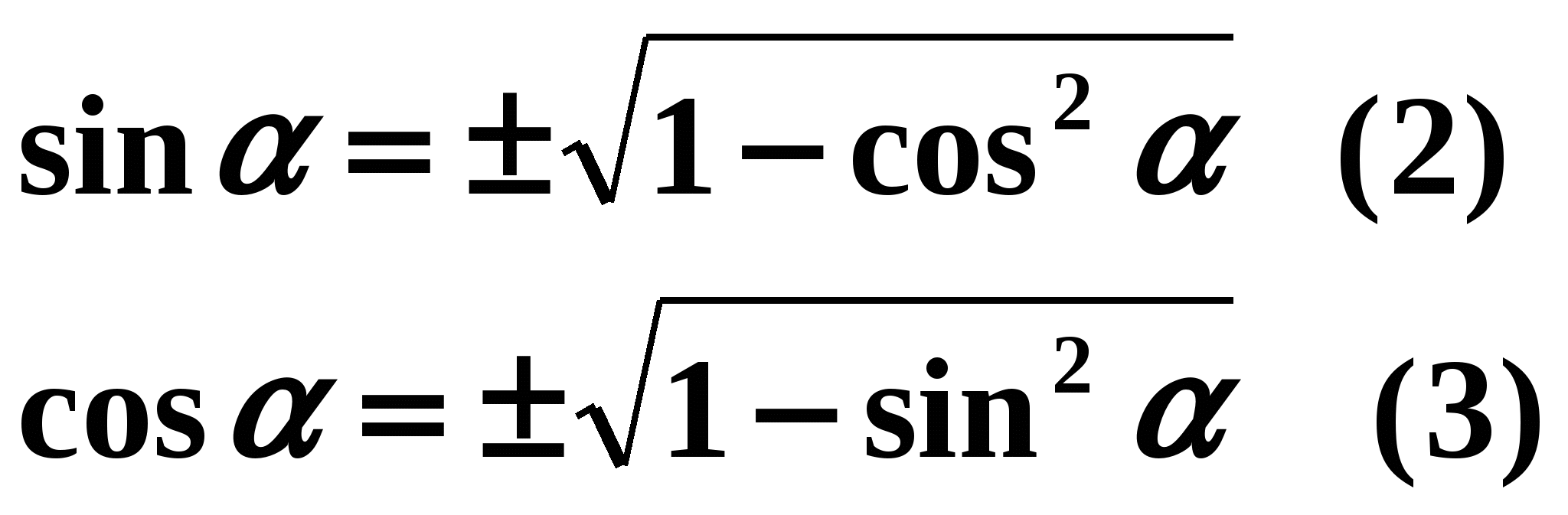 Students check their answers and score on the lesson card for Tasks number 3.
In these formulas, what does the sign in front of the root depend on? (On which quarter the angle of the trigonometric function we are defining is located).
Students check their answers and score on the lesson card for Tasks number 3.
In these formulas, what does the sign in front of the root depend on? (On which quarter the angle of the trigonometric function we are defining is located). Example 1 . Calculate
 if
if 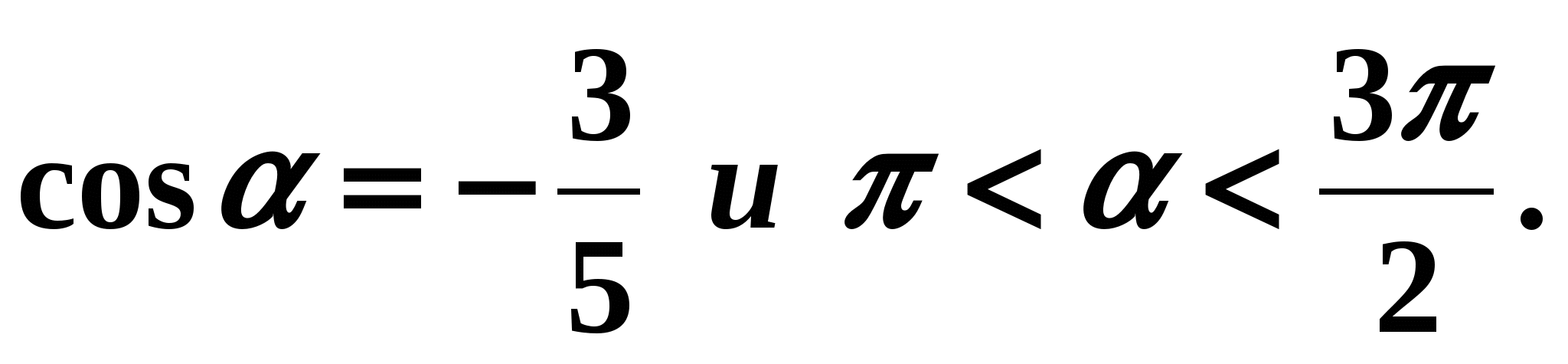 Determine the quarter in which the angle is located
Determine the quarter in which the angle is located  . Quarter - III. Recall that the sine in the third quarter is negative, i.e. in formula (2) you need to put the sign “-” before the root: Example 2
Calculate
. Quarter - III. Recall that the sine in the third quarter is negative, i.e. in formula (2) you need to put the sign “-” before the root: Example 2
Calculate 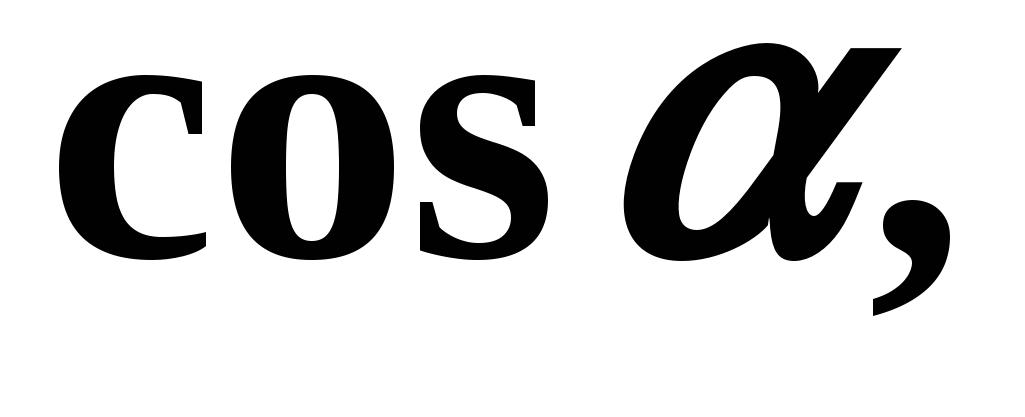 if
if  We determine the quarter in which the angle is located. Quarter - IV, the cosine in the fourth quarter is positive. Therefore, in formula (3), a “+” sign is needed before the root:
We determine the quarter in which the angle is located. Quarter - IV, the cosine in the fourth quarter is positive. Therefore, in formula (3), a “+” sign is needed before the root: Find out now relationship between tangent and cotangent. By definition of tangent and cotangent
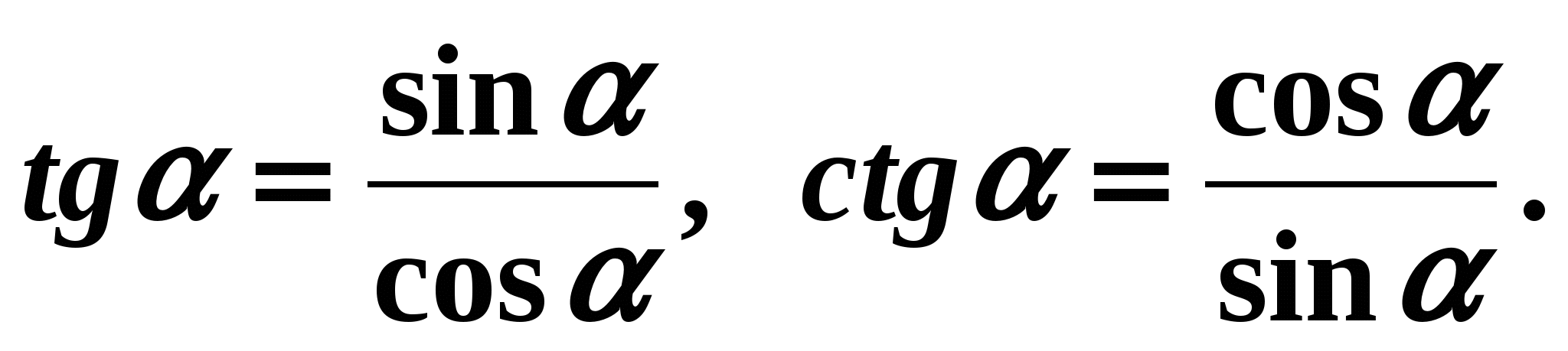
Multiplying these equalities, we get:

From equality (4) we can express
 through
through  and vice versa:
and vice versa: 
Equalities (4) - (6) are true for all values for which
 make sense, i.e. when
make sense, i.e. when 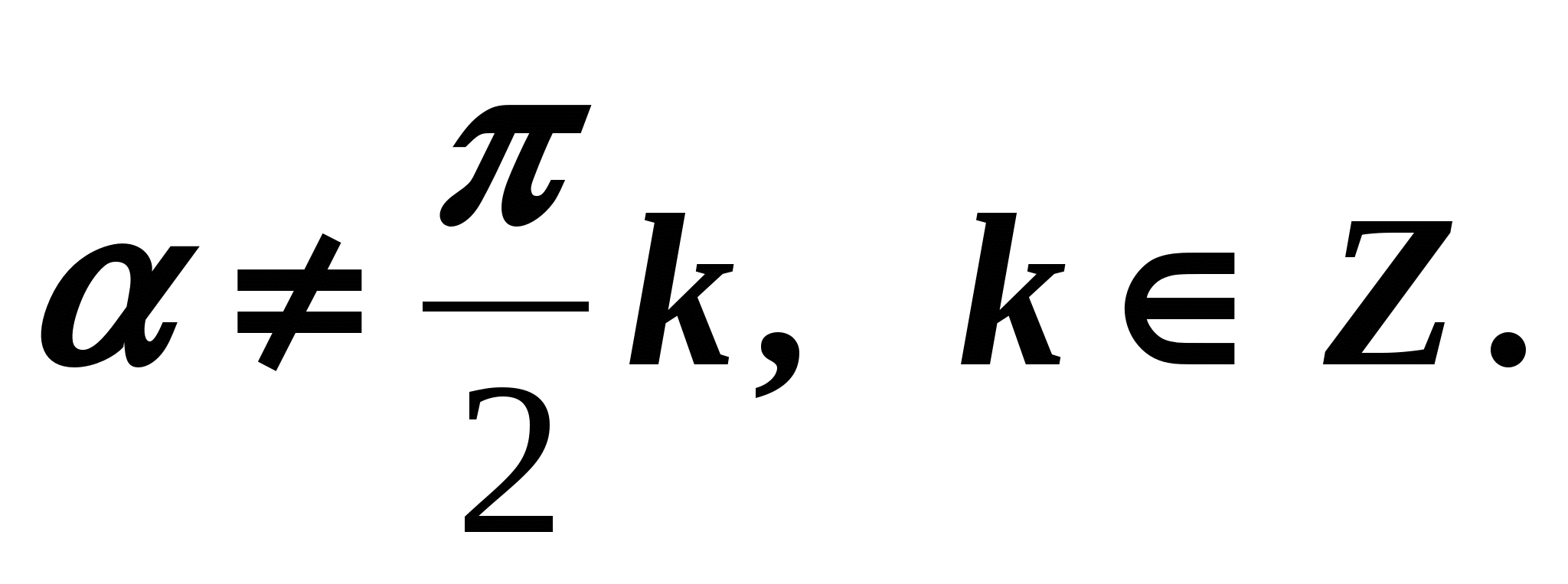 We now derive formulas expressing the relationship between the tangent and cosine, as well as the cotangent and sine of the same argument. Dividing both sides of equality (1) by
We now derive formulas expressing the relationship between the tangent and cosine, as well as the cotangent and sine of the same argument. Dividing both sides of equality (1) by 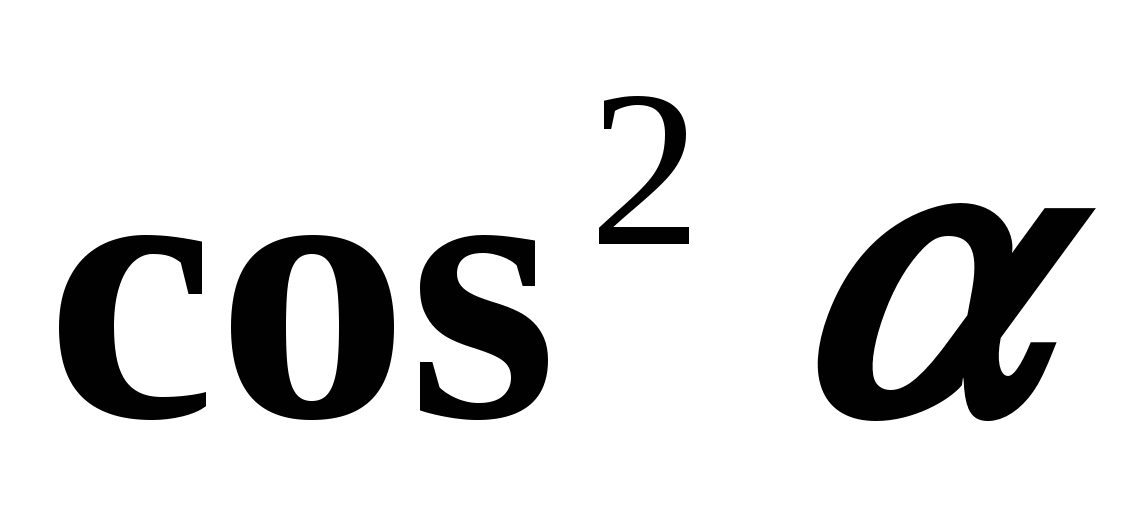 , we get:
, we get:  those.
those. 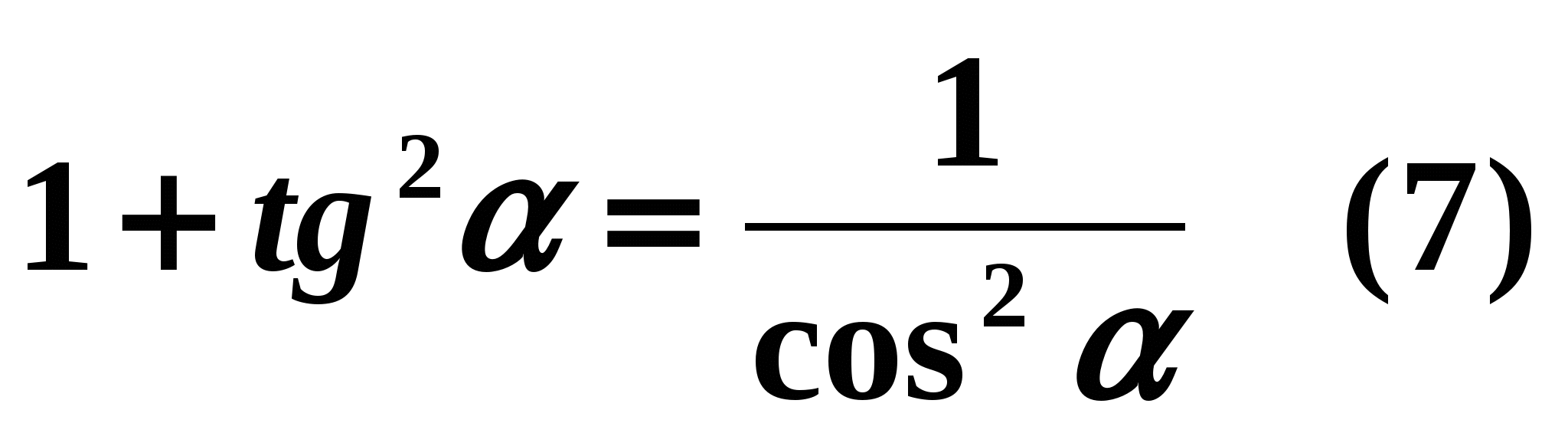
If both parts of equality (1) are divided by
 , then we will have:
, then we will have: 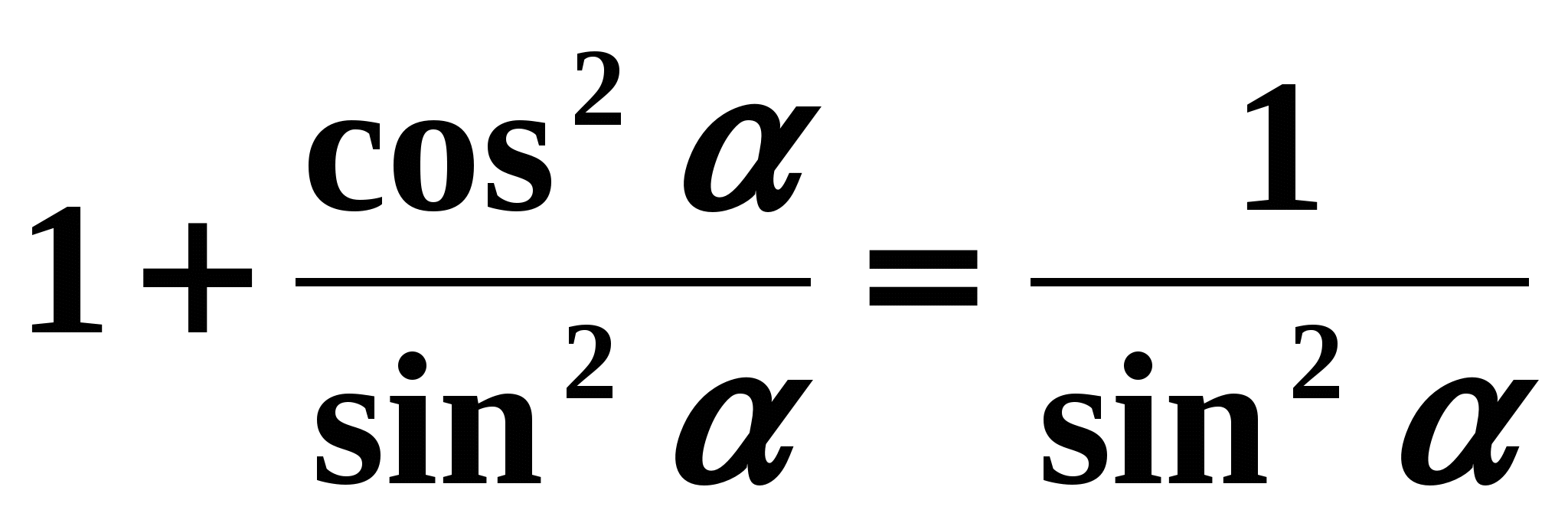 those.
those. 
Consider examples of using the derived formulas to find the values of trigonometric functions from known value one of them.
Example 1 Find if we know that
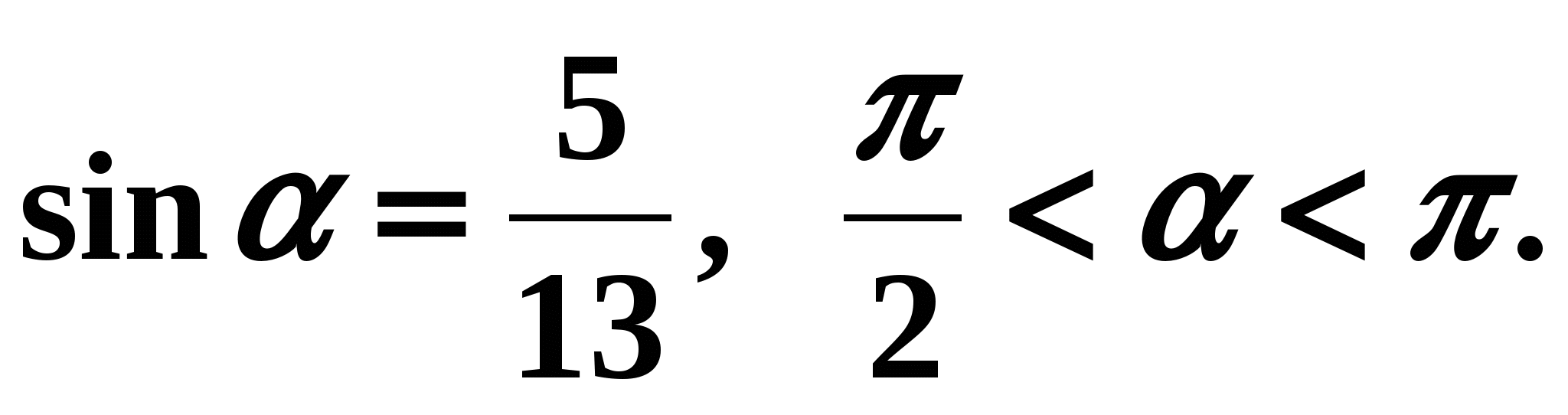 Solution:
Solution: 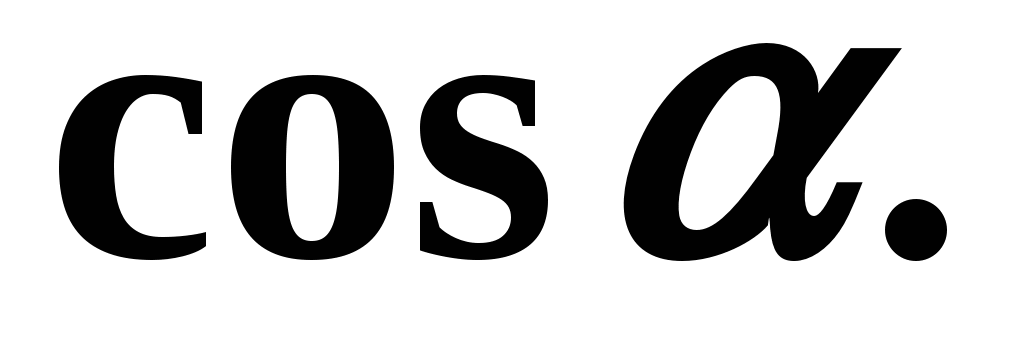
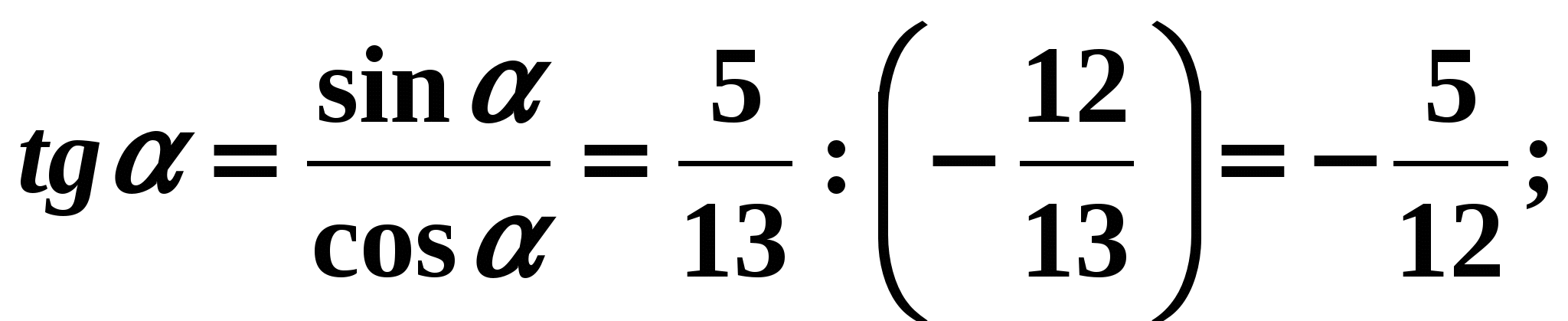
- To find the cotangent of the angle , it is convenient to use formula (6):
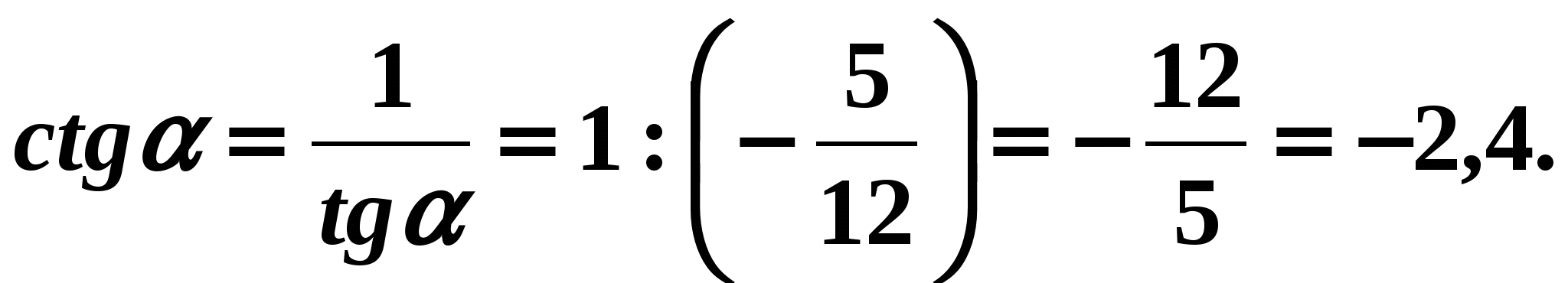 Answer:
Answer: Example2. It is known that
 . Find all other trigonometric functions. Solution:
. Find all other trigonometric functions. Solution: - Let's use the formula (7).
We have:

 ,
,  . According to the condition of the problem, the angle is the angle of 1 quarter, so its cosine is positive. Means
. According to the condition of the problem, the angle is the angle of 1 quarter, so its cosine is positive. Means 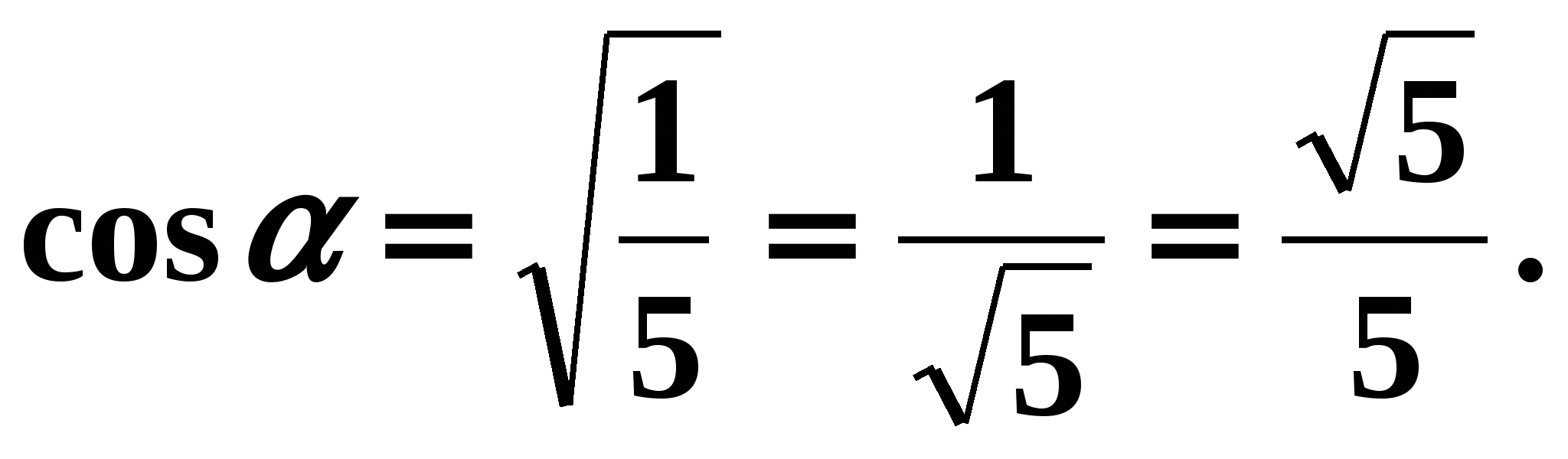

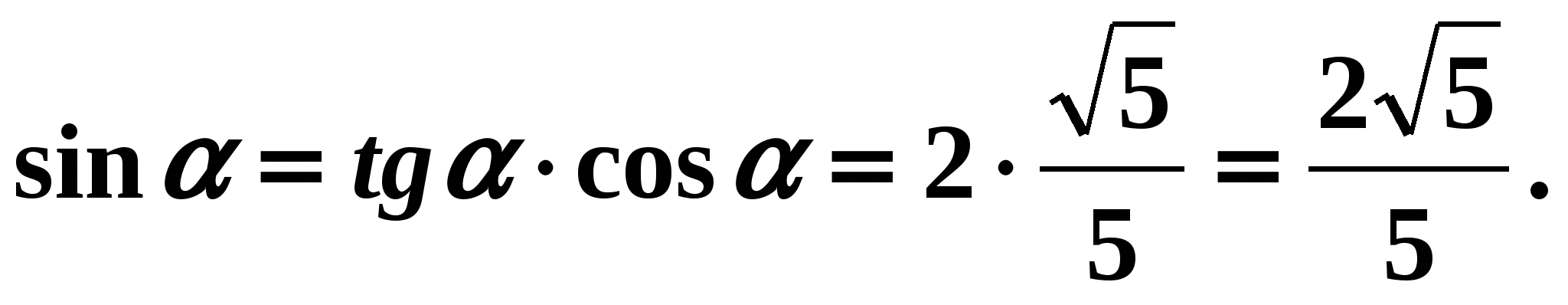
Answer:
 The established relationships between the trigonometric functions of the same argument make it possible to simplify trigonometric expressions.
The established relationships between the trigonometric functions of the same argument make it possible to simplify trigonometric expressions. Example 3 Let's simplify the expression:
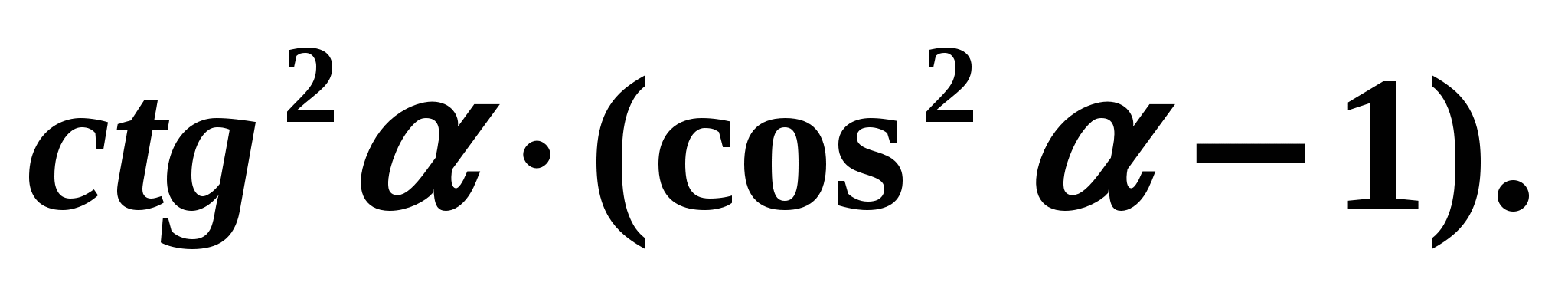 Solution: Let's use the formulas:
Solution: Let's use the formulas: 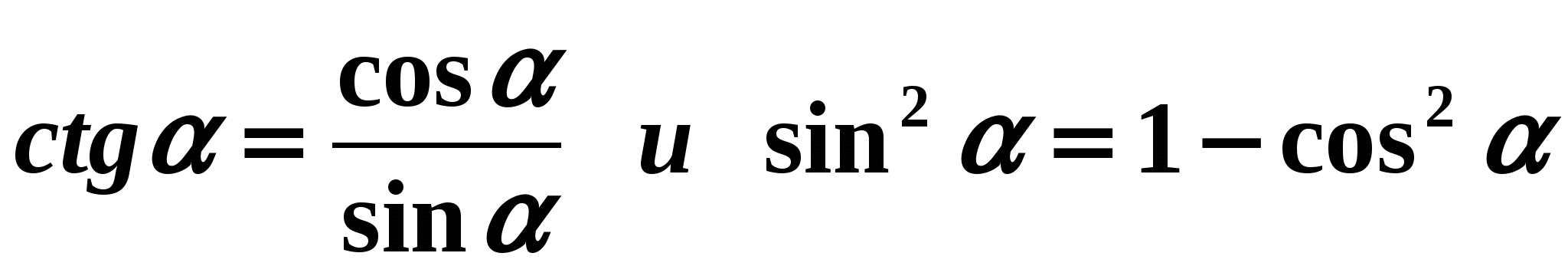 . We get:
. We get: - Consolidation.
And now on the screen are rubrics of self-assessment on this topic. Mark what level you would like to reach today.
I understand the topic and can solve examples by algorithm, looking at the notebook, but with the help of leading questions(card - instruction).
I understand the topic and can solve the examples using the algorithm, looking at the notebook, using the instructions of the teacher.
I understood the topic and can solve examples using the algorithm, looking at the notebook, without leading questions and instructions.
I understood the topic and can solve examples using the algorithm without looking at the notebook.
Whatever level you choose, first carefully review all the tasks that I gave you, and then complete the task corresponding to the level you have chosen (there are tasks of four options in front of you, the option number corresponds to the levels of self-assessment.)
1 option
 Instruction:
Instruction:
4 option
Now guys, let's check the answers. Correct answers are displayed on the screen, and students check their work and put points in the lesson card for Tasks number 4. Assess yourself on the lesson map. Calculate your scores and put them on the card.
- Homework.
- Write down all the derived formulas in the reference book. According to the textbook No. 459 (3, 5), No. 460 (1)
Let's try to find the relationship between the main trigonometric functions of the same angle.
Relationship between cosine and sine of the same angle
The following figure shows the Oxy coordinate system with a part of the unit semicircle ACB depicted in it, centered at the point O. This part is the arc of the unit circle. The unit circle is described by the equation
- x2+y2=1.
As already known, the ordinate y and the abscissa x can be represented as the sine and cosine of the angle using the following formulas:
- sin(a) = y,
- cos(a) = x.
Substituting these values into the equations of the unit circle, we have the following equality
- (sin(a)) 2 + (cos(a)) 2 =1,
This equality holds for any values of the angle a. It is called the basic trigonometric identity.
From the basic trigonometric identity, one function can be expressed in terms of another.
- sin(a) = ±√(1-(cos(a)) 2),
- cos(a) = ±√(1-(sin(a)) 2).
The sign on the right side of this formula is determined by the sign of the expression on the left side of this formula.
For example.
Calculate sin(a) if cos(a)=-3/5 and pi Let's use the formula above: Since pi Now, let's try to find the relationship between the tangent and cotangents. By definition, tg(a) = sin(a)/cos(a), ctg(a) = cos(a)/sin(a). Multiplying these equalities, we get tg(a)*ctg(a) =1. From this equality, one function can be expressed in terms of another. We get: It should be understood that these equalities are valid only when tg and ctg exist, that is, for any a, except for a = k * pi / 2, for any integer k. Now let's try using the basic trigonometric identity to find the relationship between tangent and cosine. Divide the basic trigonometric identity, by (cos(a)) 2 . (cos(a) is not equal to zero, otherwise the tangent would not exist. We get the following equality ((sin(a)) 2 + (cos(a)) 2)/ (cos(a)) 2 =1/(cos(a)) 2 . Dividing term by term we get: As noted above, this formula is true if cos(a) is not equal to zero, that is, for all angles a, except a=pi/2 + pi*k, for any integer k. A sine graph wave by wave From a student song. GOALS AND OBJECTIVES OF THE LESSON: HEALTH SAVING: creating a comfortable psychological climate in the classroom, an atmosphere of cooperation: student - teacher. METHODOLOGICAL EQUIPMENT OF THE LESSON: MATERIAL AND TECHNICAL BASE: Mathematics office. DIDACTIC SUPPORT OF THE LESSON: textbook, notebook, posters on the topic of the lesson, tables, computer, disks, screen, projector. ACTIVITY METHODS: group and individual work at the desk and at the blackboard. TYPE OF LESSON: a lesson in mastering new knowledge. DURING THE CLASSES 1. Organizational moment: greeting, checking the attendance of students, filling out the journal. 2. Checking the readiness of students for the lesson: setting the students to work, bringing the lesson plan to them. 3. Analysis of homework errors. On the screen - a picture with a correctly completed homework. Each student checks with a detailed frontal explanation and notes the correctness of the implementation in the work card of the lesson. WORKING LESSON CARD. C / o - self-esteem. O / t - assessment of a friend. 4. Actualization of knowledge, preparation for the perception of new material. The next stage of our lesson is dictation. We write down the answers briefly - the drawing is on our slide. Dictation (oral repetition of the necessary information): 1. Define: 2. Define: 3. Write down the signs of the sine, cosine, tangent, cotangent for the angles obtained by turning the point P (1; 0) by the angle 4. For all these angles, indicate the quarters of the coordinate plane. The guys check the dictation on the slide together with the teacher, explaining each statement and grading themselves on the lesson worksheet. 5. From the history of trigonometry. The modern form of trigonometry was given by the largest mathematician of the 18th century Leonard Euler- Swiss by origin, who worked in Russia for many years and was a member of the St. Petersburg Academy of Sciences. He introduced well-known definitions of trigonometric functions, formulated and proved reduction formulas that you have yet to meet, distinguished classes of even and odd functions. 6. Introduction of new material: The main thing is not just to inform the students of the final conclusions, but to make the students, as it were, participants in a scientific search: by posing a question, so that they, having awakened their curiosity, are included in the study, which contributes to the achievement of a higher level of mental development of students. Therefore, when introducing new material, I create a problematic situation - how easier and more rational to establish the relationship between the sine and cosine of the same angle - through the unit circle equation or through the Pythagorean theorem. The class is divided into options for the first and second options - on the screen there is a slide with a condition and drawings, there is no solution yet. Option 1 establishes the relationship between sine and cosine through the equation of a circle with a center at the origin and a radius equal to 1x 2 +y 2 =1; sin 2 + cos 2 =1. Option 2 establishes the relationship between sine and cosine through the Pythagorean theorem - in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs: OB 2 + AB 2 \u003d OA 2 - and we get sin 2 + cos 2 \u003d 1. They compare the results, draw conclusions: the main thing is equality is fulfilled for any values of the letters included in it? Students must answer that this is the same (the slide shows the correct solution for both the first and second options). We have obtained an equality that is valid for any values of the letters included in it. What are these equalities called? That's right - identities. Recall - what other identities do we know in algebra - the formulas for abbreviated multiplication: a 2 -b 2 \u003d (a-b) (a + b), (a-b) 2 \u003d a 2 -2ab + b 2 , (a+b) 3 =a 3 +3a 2 b+3ab 2 +b 2 , (a-b) 3 =a 3 -3a 2 b+3ab 3 -b 3 , a 3 -b 3 \u003d (a-b) (a 2 + ab + b 2), a 3 + b 3 \u003d (a + b) (a 2 -ab + b 2). The next problem - why did we derive the main trigonometric identity - sin 2 + cos 2 =1. That's right - to find one known value of the sine, cosine or tangent - the values of all other functions. Now we can always use the basic trigonometric identity, but the main thing is for the same argument. Application of acquired knowledge: OPTION 1 - Express the sine in terms of the cosine of the angle. Option 2 - Express the cosine in terms of the sine of the angle. The correct answer is on the slide. Question of the teacher - no one forgot to put down the + and - signs? What could be the angle? - anyone. In these formulas, the sign in front of the root depends on what? on which quarter the angle (argument) of the trigonometric function that we are defining is located. We perform at the blackboard 2 students No. 457. - 1st option - 1, 2nd option - 2. The slide shows the correct answer. Independent work on recognition of the basic trigonometric identity 1. find the value of the expression: 2. express the number 1 through the angle a, if There is a mutual check - according to the finished slide and evaluation of the work - both by self-assessment and by the assessment of a friend. 6. Consolidation of new material (according to the technology of G.E. Khazankin - technology of supporting tasks). PROBLEM 1. Calculate ……….. if …………………………………………………………………. 1 student at the blackboard on their own - then slide with the correct solution. TASK 2. Calculate……………., if……………………………………………………………….. 2nd student at the blackboard, then slide with the correct solution. 7. Physical education. I know that you are already adults and think that you are not tired at all, especially now, when the lesson is so active that the time for us seems to be lengthening - according to A. Einstein's theory of relativity, but let's do gymnastics for cerebral vessels: Let us now find out the relationship between the tangent and the cotangent………………………………………………………………………………………………………… There is a new study on the topic - what can be the angle in the second trigonometric identity? THE MAIN THING IS CLAIMING THE SET ON WHICH THESE EQUALITIES ARE CARRIED OUT. MARK ON THE PICTURE THE POINTS WHERE THE TANGENT AND COTENGENCE OF THE ANGLE DO NOT EXIST. 3rd student at the blackboard. The equalities are valid for………………………. TASK3. Calculate……… if…………………………. TASK 4. Calculate…………….. if ……………………………………………………………… The rest of the students work in their notebooks. 1 SUPPORT………………………………………………………………………………………………… 2 SUPPORT………………………………………………………………………………………………… 3 SUPPORT. Application of the basic trigonometric identity to problem solving. 8. Crossword. Anatole France once said: "Learning should be fun ... To digest knowledge, you need to absorb it with appetite." To test your knowledge on this topic, you are offered a crossword puzzle. After checking the crossword puzzle, the guys give themselves grades in the work card of the lesson. The teacher grades those students who are especially active in the lesson. The result is the average score for the work in the lesson. 9. Instructing the teacher to do homework. 10. Summing up the lesson by the teacher. 11. Homework: paragraph 25 (before task 5), No. 459 (even), 460 (even), 463 * (4). Textbook Sh.A Alimov "Algebra and the beginning of analysis", 10-11, "Enlightenment", M., 2005. LESSON MAP "DEPENDENCE BETWEEN SINE, COSINE AND TANGENT OF THE SAME ANGLE" Student _____________________________________________________________________________ 1. I know the material from previous lessons Points I answered all the questions correctly without an outline. I answered without a synopsis with one mistake. I answered without an outline and made more than one mistake. I answered all the questions correctly using the abstract. I answered using abstract, with one mistake I answered using the abstract and made more than one mistake 2. I have finished recording examples Points I completed all tasks without errors I completed with one error I completed the tasks and made more than two mistakes 3. I completed the derivation of the formula for finding the sine and cosine Points I got the formula right I deduced the formulas and made one mistake I deduced the formulas with the help of a teacher 4. I applied my knowledge on the topic: "The relationship between sine, cosine and tangent of the same angle" when solving independent work Points I solved the examples of option 1 without errors. I solved the examples of option 1 and made a mistake. I solved examples 2 options without errors. I solved examples 2 options and made a mistake. I solved examples 3 options without errors I solved the examples of 3 options and made a mistake. I solved examples 4 options without errors. I solved the examples of 4 options and made a mistake. 5. Rate yourself: I understood the derivation of formulas and can solve examples on this topic with a notebook and the help of a teacher. I understood the derivation of formulas and I can solve examples on my own without a notebook, just looking at the formulas. I understood the derivation of formulas and I can solve examples on my own without a notebook, if I forget the formula, I can deduce it myself. My scores: __________ Maximum points - 22 18 - 22 points - score "5" 15 - 17 points - score "4" 11–14 points - grade "3" Less than 11 points - you need to come for a consultation in the coming days, the material has not yet been mastered. Golovatova Vera Anatolyevna, teacher of mathematics GB POU "Okhta College" Summary of two lessons for studentsI
course (10kl.) on the topic: "Relationship between sine, cosine and tangent of the same angle" Target: study the relationship between the sine, cosine and tangent of the same angle. To achieve this goal it is necessary: Know: formulations of definitions of the main trigonometric functions (sine, cosine and tangent); signs of trigonometric functions in quarters; set of values of trigonometric functions; basic formulas of trigonometry. Understand: that the basic trigonometric identity can only be used for one and the same argument; algorithm for calculating one trigonometric function through another. Apply: the ability to choose the right formula for solving a specific task; ability to work with simple fractions; the ability to perform the transformation of trigonometric expressions. Analysis: analyze errors in the logic of reasoning. Synthesis: offer your own way of solving examples; make a crossword puzzle using the knowledge gained. Grade: knowledge and skills on this topic for use in other sections of algebra. Equipment:
layout of a trigonometric circle, handouts with formulas and tables of values of trigonometric functions, computer, multimedia projector, presentation, worksheets for self-study. Sources used: Algebra and the Beginnings of Analysis: A Textbook for Grades 10-11. general education institutions / Sh.A. Alimov, Yu.V. Sidorov et al. Education, 2006. Tasks of the Open Bank for preparing for the exam in mathematics, 2011 Internet resources. Short lesson plan: Organizing time. Greetings. Communication of the purpose of the lesson and the plan of work in the lesson - 3-5 min. Updating knowledge and skills. Students are given lesson cards and explained how to work with them. Questions are displayed on the screen; students write their answers in a notebook; The teacher displays the correct answer on the screen. After the end of the survey, students put points in the lesson card for Tasks number 1
– 10 min. Explanation of new material. The teacher derives the formula for the basic trigonometric identity - 5 minutes. Students are invited to independently complete the recording of examples displayed on the screen, check the correctness of the answers and put points on the lesson card for Tasks number 2 -
5 minutes. Students in the notebook are invited to independently express from the basic trigonometric identity the sine through the cosine and the cosine through the sine. The correct answer is displayed on the screen, students check and put points in the lesson card for Tasks №3
– 5-7 min. The teacher on the blackboard solves examples on the application of the basic trigonometric identity. Students answer the teacher's questions as they explain and write examples in their notebooks - 15 minutes. The teacher derives formulas showing the relationship between tangent and cotangent, students take an active part in the derivation of formulas, answer questions and make notes in a notebook - 5 minutes. The teacher derives formulas showing the relationship between tangent and cosine, between sine and cotangent - 5 minutes. Students are called to the board at will and, with the help of a teacher, solve examples using an algorithm. Everyone else takes notes and answers questions as needed – 10 min. Consolidation of the studied material At the end of the lesson, the correct answers are displayed on the screen, students check their answers and put points in the lesson card for Tasks number 4
– 20 minutes. Homework: Students write homework assignments in their notebooks. 3 min. After attending seminars on RNS and conducting a lesson using a technological map, it became obvious to me that the rating system stimulates the maximum possible interest of students in a particular topic. In my case, these are the basic formulas of trigonometry. Trigonometry is very often not perceived by students, not so much because of its complexity, but because of the large number of formulas that you need to be able to work with. It is difficult to expect some incredible progress and results after one lesson, conducted using a technological map, but it seems to me that the advantages of the rating system in the study of trigonometry and mathematics in general are as follows: it became possible to organize and support both work in the classroom and independent, systematic work of students at home; attendance and the level of discipline in the classroom should increase; increases motivation for learning activities; stressful situations are reduced when receiving unsatisfactory grades; encourages creativity at work. The only drawback of the RNS (as it seems to me) is a large amount of work for the teacher, but this is work for the result. After a single lesson with this system, students constantly ask if we will continue to work this way. It means that they are hooked on something. And we need to keep working. INDEPENDENT WORK Whatever level you choose, first carefully review all the tasks that I gave you, and then complete the task corresponding to the level you have chosen (there are four options for you, the number of the option corresponds to the levels of self-assessment.) 1 option
Instruction:
Instruction:
Solve this example for yourself: Option 2
Note: To determine the cosine function, use formula (3) from today's lesson. Don't forget to define the sign that will come before the root. To calculate the values of tangent and cotangent, you can use the definition of these functions or use the formulas that we derived today in the lesson. Instruction. Group the first and third terms of the expression, bracket the common factor .... 3 option
4 option
Repetition: 1. What quarter is the angle in 1 radian and what is it approximately equal to? In the first quarter, 1 glad. 57.3° 2. What word is missing in the definition of the sine function? The sine of an angle
is called ………… points of the unit circle. ORDINATE 3. What word is missing in the definition of the cosine function? Cosine of an angle
called …………
points of the unit circle. ABSCISSA 4. Add the formula:
tg
5. Determine the sign of the product: tg
6. What value can the sine take?
or
7. Calculate: y
B(x;y)
R
Y=sin
O
x
x=cos
Finish recording:
x
y
x
y
x
x
x
y
x
y
x
x
1 Option: 3 option: Option 2: 4 Option:The ratio between the tangent and cotangent of the same angle
The abscissa runs away.


"Short Plan"View document content
"Reflection"View document content
"Independent work"





View presentation content
"Presentation"

















