Matrices. Types of matrices. Operations on matrices and their properties.
Determinant of an nth order matrix. N, Z, Q, R, C,
A matrix of order m*n is a rectangular table of numbers containing m-rows and n-columns.
Matrix equality:
Two matrices are said to be equal if the number of rows and columns of one of them is equal to the number of rows and columns of the other, respectively. The elements of these matrices are equal.
Note: E-mails having the same indexes are corresponding.
Types of matrices:
Square matrix: A matrix is called square if the number of its rows is equal to the number of columns.
Rectangular: A matrix is called rectangular if the number of rows is not equal to the number of columns.
Row matrix: a matrix of order 1*n (m=1) has the form a11,a12,a13 and is called a row matrix.
Matrix column:………….
Diagonal: The diagonal of a square matrix, going from the upper left corner to the lower right corner, that is, consisting of elements a11, a22...... is called the main diagonal. (definition: a square matrix whose elements are all zero, except those located on the main diagonal, is called a diagonal matrix.
Identity: A diagonal matrix is called identity matrix if all elements are located on the main diagonal and are equal to 1.
Upper triangular: A=||aij|| is called an upper triangular matrix if aij=0. Provided i>j.
Lower triangular: aij=0. i Zero: this is a matrix whose values are equal to 0. Operations on matrices. 1.Transposition. 2.Multiplying a matrix by a number. 3. Addition of matrices.
4.Matrix multiplication.
Basic properties of actions on matrices.
1.A+B=B+A (commutativity)
2.A+(B+C)=(A+B)+C (associativity)
3.a(A+B)=aA+aB (distributivity)
4.(a+b)A=aA+bA (distributive)
5.(ab)A=a(bA)=b(aA) (asoc.)
6.AB≠BA (no comm.)
7.A(BC)=(AB)C (associat.) – executed if defined. Matrix products are performed.
8.A(B+C)=AB+AC (distributive)
(B+C)A=BA+CA (distributive)
9.a(AB)=(aA)B=(aB)A
Determinant of a square matrix – definition and its properties. Decomposition of the determinant into rows and columns. Methods for calculating determinants.
If matrix A has order m>1, then the determinant of this matrix is a number.
The algebraic complement Aij of the aij element of matrix A is the minor Mij multiplied by the number
THEOREM1: Determinant of matrix A equal to the sum products of all elements of an arbitrary row (column) by their algebraic complements.
Basic properties of determinants.
1. The determinant of a matrix will not change when it is transposed.
2. When rearranging two rows (columns), the determinant changes sign, but its absolute value does not change.
3. The determinant of a matrix that has two identical rows (columns) is equal to 0.
4. When a row (column) of a matrix is multiplied by a number, its determinant is multiplied by this number.
5. If one of the rows (columns) of the matrix consists of 0, then the determinant of this matrix is equal to 0.
6. If all elements of the i-th row (column) of a matrix are presented as the sum of two terms, then its determinant can be represented as the sum of the determinants of two matrices.
7. The determinant will not change if the elements of one column (row) are added to the elements of another column (row), respectively, after multiplying. for the same number.
8. The sum of arbitrary elements of any column (row) of the determinant by the corresponding algebraic complement of the elements of another column (row) is equal to 0.
https://pandia.ru/text/78/365/images/image004_81.gif" width="46" height="27">
Methods for calculating the determinant:
1. By definition or Theorem 1.
2. Reduction to triangular form.
Definition and properties of an inverse matrix. Calculation of the inverse matrix. Matrix equations.
Definition: A square matrix of order n is called the inverse of matrix A of the same order and is denoted
In order for matrix A to exist inverse matrix It is necessary and sufficient that the determinant of the matrix A be different from 0.
Properties of an inverse matrix:
1. Uniqueness: for a given matrix A, its inverse is unique.
2. matrix determinant
3. The operation of taking transposition and taking the inverse matrix.
Matrix equations:
Let A and B be two square matrices of the same order.
https://pandia.ru/text/78/365/images/image008_56.gif" width="163" height="11 src=">
Concept linear dependence and independence of matrix columns. Properties of linear dependence and linear independence of a column system.
Columns A1, A2...An are called linearly dependent if there is a non-trivial linear combination of them equal to the 0th column.
Columns A1, A2...An are called linearly independent if there is a non-trivial linear combination of them equal to the 0th column.
A linear combination is called trivial if all coefficients C(l) are equal to 0 and non-trivial otherwise.
https://pandia.ru/text/78/365/images/image010_52.gif" width="88" height="24">
2. In order for the columns to be linearly dependent, it is necessary and sufficient that some column be a linear combination of other columns.

Let 1 of the columns https://pandia.ru/text/78/365/images/image014_42.gif" width="13" height="23 src=">be a linear combination of other columns.
https://pandia.ru/text/78/365/images/image016_38.gif" width="79" height="24"> are linearly dependent, then all columns are linearly dependent.
4. If a system of columns is linearly independent, then any of its subsystems is also linearly independent.
(Everything that is said about columns is also true for rows).
Matrix minors. Basic minors. Matrix rank. Method of bordering minors for calculating the rank of a matrix.
A minor of order k of a matrix A is a determinant whose elements are located at the intersection of the k-rows and k-columns of the matrix A.
If all minors of the kth order of the matrix A = 0, then any minor of order k+1 is also equal to 0.
Basic minor.
The rank of a matrix A is the order of its basis minor.
Method of bordering minors: - Select a non-zero element of matrix A (If such an element does not exist, then rank A = 0)
We border the previous 1st order minor with a 2nd order minor. (If this minor is not equal to 0, then the rank is >=2) If the rank of this minor is =0, then we border the selected 1st order minor with other 2nd order minors. (If all minors of the 2nd order = 0, then the rank of the matrix = 1).
Matrix rank. Methods for finding the rank of a matrix.
The rank of a matrix A is the order of its basis minor.
Calculation methods:
1) Method of bordering minors: - Select a non-zero element of matrix A (if there is no such element, then rank = 0) - Border the previous 1st order minor with a 2nd order minor..gif" width="40" height="22" >r+1 Mr+1=0.
2) Reducing the matrix to a stepwise form: this method is based on elementary transformations. During elementary transformations, the rank of the matrix does not change.
The following transformations are called elementary transformations:
Rearranging two rows (columns).
Multiplying all elements of a certain column (row) by a number not =0.
Adding to all elements of a certain column (row) the elements of another column (row), previously multiplied by the same number.
The theorem on the basis minor. A necessary and sufficient condition for the determinant to be equal to zero.
The basis minor of a matrix A is the minor of the highest kth order different from 0.
The basis minor theorem:
The underlying rows (columns) are linearly independent. Any row (column) of matrix A is a linear combination of the basis rows (columns).
Notes: Rows and columns at the intersection of which there is a basis minor are called basis rows and columns, respectively.
a11 a12… a1r a1j
a21 a22….a2r a2j
a31 a32….a3r a3j
ar1 ar2….arr arj
ak1 ak2…..akr akj
Necessary and sufficient conditions for the determinant to be equal to zero:
In order for a determinant of nth order to =0, it is necessary and sufficient that its rows (columns) be linearly dependent.
Systems linear equations, their classification and recording forms. Cramer's rule.
Consider a system of 3 linear equations with three unknowns:
https://pandia.ru/text/78/365/images/image020_29.gif" alt="l14image048" width="64" height="38 id=">!}
is called the determinant of the system.
Let's compose three more determinants as follows: replace sequentially 1, 2 and 3 columns in the determinant D with a column of free terms
https://pandia.ru/text/78/365/images/image022_23.gif" alt="l14image052" width="93" height="22 id=">!}
Proof. So, let's consider a system of 3 equations with three unknowns. Let's multiply the 1st equation of the system by the algebraic complement A11 of the element a11, the 2nd equation by A21 and the 3rd by A31:
https://pandia.ru/text/78/365/images/image024_24.gif" alt="l14image056" width="247" height="31 id=">!}
Let's look at each of the brackets and the right side of this equation. By the theorem on the expansion of the determinant in elements of the 1st column
https://pandia.ru/text/78/365/images/image026_23.gif" alt="l14image060" width="324" height="42 id=">!}
Similarly, it can be shown that and .
Finally, it is easy to notice that ![]()
Thus, we obtain the equality: .
Hence, .
The equalities and are derived similarly, from which the statement of the theorem follows.
Systems of linear equations. Condition for compatibility of linear equations. Kronecker-Capelli theorem.
System solution algebraic equations such a set of n numbers C1,C2,C3……Cn is called, which, when substituted into the original system in place of x1,x2,x3…..xn, turns all the equations of the system into identities.
A system of linear algebraic equations is called consistent if it has at least one solution.
A consistent system is called determinate if it has a unique solution, and indefinite if it has infinitely many solutions.
Consistency conditions for systems of linear algebraic equations.
a11 a12 ……a1n x1 b1
a21 a22 ……a2n x2 b2
……………….. .. = ..
am1 am2…..amn xn bn
THEOREM: In order for a system of m linear equations with n unknowns to be consistent, it is necessary and sufficient that the rank of the extended matrix be equal to the rank of matrix A.
Note: This theorem only provides criteria for the existence of a solution, but does not indicate a method for finding a solution.
10 question.
Systems of linear equations. Basic minor method - general method finding all solutions to systems of linear equations.

A=a21 a22…..a2n
Basic minor method:
Let the system be consistent and RgA=RgA’=r. Let the basis minor be written in the upper left corner of the matrix A.
https://pandia.ru/text/78/365/images/image035_20.gif" width="22" height="23 src=">......gif" width="23" height="23 src= ">…...gif" width="22" height="23 src=">......gif" width="46" height="23 src=">-…..-a
d2 b2-a(2r+1)x(r+1)-..-a(2n)x(n)
… = …………..
Dr br-a(rr+1)x(r+1)-..-a(rn)x(n)
https://pandia.ru/text/78/365/images/image050_12.gif" width="33" height="22 src=">
Notes: If the rank of the main matrix and the matrix under consideration is equal to r=n, then in this case dj=bj and the system has a unique solution.
Homogeneous systems of linear equations.
A system of linear algebraic equations is called homogeneous if all its free terms are equal to zero.
![]()
AX=0 – homogeneous system.
AX =B is a heterogeneous system.
Homogeneous systems are always consistent.
X1 =x2 =..=xn =0
Theorem 1.
Homogeneous systems have inhomogeneous solutions when the rank of the system matrix less number unknown.
Theorem 2.
Homogeneous system n-linear equations with n-unknowns has a non-zero solution when the determinant of matrix A is equal to zero. (detA=0)
Properties of solutions of homogeneous systems.
Any linear combination of solutions homogeneous system itself is a solution to this system.
α1C1 +α2C2 ; α1 and α2 are some numbers.
A(α1C1 +α2C2) = A(α1C1) +A(α2C2) = α1(A C1) + α2(AC2) = 0, i.e. k. (A C1) = 0; (AC2) = 0
For an inhomogeneous system this property does not hold.
Fundamental system of solutions.
Theorem 3.
If the rank of a matrix system of an equation with n-unknowns is equal to r, then this system has n-r linearly independent decisions.
Let the base minor be in the upper left corner. If r< n, то неизвестные х r+1;хr+2;..хn называются свободными переменными, а систему уравнений АХ=В запишем, как Аr Хr =Вr
![]()
C1 = (C11 C21 .. Cr1 , 1,0..0)
C2 = (C21 C22 .. C2r,0, 1..0)<= Линейно-независимы.
……………………..
Cn-r = (Cn-r1 Cn-r2 .. Cn-rr ,0, 0..1)
A system of n-r linearly independent solutions to a homogeneous system of linear equations with n-unknowns of rank r is called a fundamental system of solutions.
Theorem 4.
Any solution to a system of linear equations is a linear combination of a solution to the fundamental system.
С = α1C1 +α2C2 +.. + αn-r Cn-r
If r Question 12. General solution of a heterogeneous system. Sleep (general heterogeneous) = Coo + Sch (particular) AX=B (heterogeneous system); AX= 0 (ASoo) + ASch = ASch = B, because (ASoo) = 0 Sleep= α1C1 +α2C2 +.. + αn-r Cn-r + Sch Gauss method. This is a method of sequential elimination of unknowns (variables) - it consists in the fact that, with the help of elementary transformations, the original system of equations is reduced to an equivalent system of a stepwise form, from which all other variables are found sequentially, starting with the last variables. Let a≠0 (if this is not the case, then this can be achieved by rearranging the equations). 1) we exclude the variable x1 from the second, third...nth equation, multiplying the first equation by suitable numbers and adding the results obtained to the 2nd, 3rd...nth equation, then we get: We obtain a system equivalent to the original one. 2) exclude the variable x2 3) exclude the variable x3, etc. Continuing the process of sequentially eliminating the variables x4;x5...xr-1 we obtain for the (r-1)th step. The number zero of the last n-r in the equations means that their left side has the form: 0x1 +0x2+..+0xn If at least one of the numbers br+1, br+2... is not equal to zero, then the corresponding equality is contradictory and system (1) is not consistent. Thus, for any consistent system this br+1 ... bm is equal to zero. The last n-r equation in the system (1;r-1) are identities and can be ignored. There are two possible cases: a) the number of equations of the system (1;r-1) is equal to the number of unknowns, i.e. r=n (in this case the system has a triangular form). b)r The transition from system (1) to the equivalent system (1;r-1) is called the direct move of the Gaussian method. Finding a variable from the system (1;r-1) is the reverse of the Gaussian method. It is convenient to carry out Gaussian transformations by performing them not with equations, but with an extended matrix of their coefficients. Question 13. Similar matrices. We will consider only square matrices of order n/ A matrix A is said to be similar to matrix B (A~B) if there exists a non-singular matrix S such that A=S-1BS. Properties of similar matrices. 1) Matrix A is similar to itself. (A~A) If S=E, then EAE=E-1AE=A 2) If A~B, then B~A If A=S-1ВS => SAS-1= (SS-1)B(SS-1)=B 3) If A~B and at the same time B~C, then A~C It is given that A=S1-1BS1, and B=S2-1CS2 => A= (S1-1 S2-1) C(S2 S1) = (S2 S1)-1C(S2 S1) = S3-1CS3, where S3 = S2S1 4) The determinants of similar matrices are equal. Given that A~B, it is necessary to prove that detA=detB. A=S-1 BS, detA=det(S-1 BS)= detS-1* detB* detS = 1/detS *detB*detS (reduced) = detB. 5) The ranks of similar matrices coincide. Eigenvectors and eigenvalues matrices The number λ is called an eigenvalue of matrix A if there is a non-zero vector X (matrix column) such that AX = λ X, vector X is called an eigenvector of matrix A, and the set of all eigenvalues is called the spectrum of matrix A. Properties of eigenvectors. 1) When multiplying an eigenvector by a number, we obtain an eigenvector with the same eigenvalue. AX = λ X; X≠0 α X => A(α X) = α (AX) = α(λ X) = = λ (αX) 2) Eigenvectors with pairwise different eigenvalues are linearly independent λ1, λ2,.. λк. Let the system consist of 1 vector, let’s take an inductive step: С1 Х1 +С2 Х2 + .. +Сn Хn = 0 (1) – multiply by A. C1 AX1 +C2 AX2 + .. +Cn AXn = 0 С1 λ1 Х1 +С2 λ2 Х2 + .. +Сn λn Хn = 0 Multiply by λn+1 and subtract С1 Х1 +С2 Х2 + .. +Сn Хn+ Сn+1 Хn+1 = 0 С1 λ1 Х1 +С2 λ2 Х2 + .. +Сn λn Хn+ Сn+1 λn+1 Хn+1 = 0 C1 (λ1 –λn+1)X1 + C2 (λ2 –λn+1)X2 +.. + Cn (λn –λn+1)Xn + Cn+1 (λn+1 –λn+1)Xn+1 = 0 C1 (λ1 –λn+1)X1 + C2 (λ2 –λn+1)X2 +.. + Cn (λn –λn+1)Xn = 0 It is necessary that C1 = C2 =... = Cn = 0 Сn+1 Хn+1 λn+1 =0 Characteristic equation. A-λE is called the characteristic matrix for matrix A. In order for a non-zero vector X to be an eigenvector of the matrix A, corresponding to the eigenvalue λ, it is necessary that it be a solution to a homogeneous system of linear algebraic equations (A - λE)X = 0 The system has a nontrivial solution when det (A - XE) = 0 - this is the characteristic equation. Statement! The characteristic equations of such matrices coincide. det(S-1AS – λE) = det(S-1AS – λ S-1ЕS) =det(S-1 (A – λE)S) = det S-1 det(A – λE) detS= det(A – λE) Characteristic polynomial. det(A – λE) - function relative to the parameter λ det(A – λE) = (-1)n Xn +(-1)n-1(a11+a22+..+ann)λn-1+..+detA This polynomial is called the characteristic polynomial of matrix A. Consequence: 1) If the matrices are A~B, then the sum of their diagonal elements coincides. a11+a22+..+ann = в11+в22+..+вnn 2) The set of eigenvalues of similar matrices coincide. If the characteristic equations of the matrices coincide, then they are not necessarily similar. For matrix A For matrix B https://pandia.ru/text/78/365/images/image062_10.gif" width="92" height="38"> Det(Ag-λE) = (λ11 – λ)(λ22 – λ)…(λnn – λ)= 0 In order for a matrix A of order n to be diagonalizable, it is necessary that there exist linearly independent eigenvectors of the matrix A. Consequence. If all the eigenvalues of a matrix A are different, then it is diagonalizable. Algorithm for finding eigenvectors and eigenvalues. 1) compose a characteristic equation 2) find the roots of the equations 3) we compose a system of equations to determine the eigenvector. λi (A-λi E)X = 0 4) find a fundamental system of solutions x1,x2..xn-r, where r is the rank of the characteristic matrix. r =Rg(A - λi E) 5) eigenvector, eigenvalues λi are written as: X = С1 Х1 +С2 Х2 + .. +Сn-r Хn-r, where С12 +С22 +… С2n ≠0 6) check whether the matrix can be reduced to diagonal form. 7) find Ag Ag = S-1AS S= Question 15. The basis of a straight line, plane, space. DIV_ADBLOCK410"> The modulus of a vector is its length, that is, the distance between A and B (││, ││). The modulus of a vector is zero when this vector is zero (│ō│=0) 4. Orth vector. An orth of a given vector is a vector that has the same direction as the given vector and has a modulus equal to one. Equal vectors have equal vectors. 5.Angle between two vectors. This is a smaller part of the area, limited by two rays emanating from the same point and directed in the same way with the given vectors. Vector addition. Multiplying a vector by a number. 1) Addition of two vectors https://pandia.ru/text/78/365/images/image065_9.gif" height="11">+ │≤│ │+│ │ 2)Multiplying a vector by a scalar. The product of a vector and a scalar is a new vector that has: a) = product of the modulus of the vector being multiplied by the absolute value of the scalar. b) the direction is the same as the vector being multiplied if the scalar is positive, and opposite if the scalar is negative. λ а(vector)=>│ λ │= │ λ │=│ λ ││ │ Properties of linear operations on vectors. 1. The law of communicability. 2. Law of associativity. 3. Addition with zero. a(vector)+ō= a(vector) 4. Addition with the opposite. 5. (αβ) = α(β) = β(α) 6;7.The law of distributivity. Expressing a vector in terms of its modulus and orth. The maximum number of linearly independent vectors is called a basis. A basis on a line is any non-zero vector. A basis on the plane is any two non-callenary vectors. A basis in space is a system of any three non-coplanar vectors. The coefficient of expansion of a vector over a certain basis is called the components or coordinates of the vector in this basis. https://pandia.ru/text/78/365/images/image075_10.gif" height="11 src=">.gif" height="11 src="> perform the action of addition and multiplication by a scalar, then as a result any number of such actions we get: λ1 https://pandia.ru/text/78/365/images/image079_10.gif" height="11 src=">+...gif" height="11 src=">.gif" height="11 src="> are called linearly dependent if there is a nontrivial linear combination of them equal to ō. λ1 https://pandia.ru/text/78/365/images/image079_10.gif" height="11 src=">+...gif" height="11 src=">.gif" height="11 src="> are called linearly independent if there is no non-trivial linear combination of them. Properties of linearly dependent and independent vectors: 1) a system of vectors containing a zero vector is linearly dependent. λ1 https://pandia.ru/text/78/365/images/image079_10.gif" height="11 src=">+...gif" height="11 src=">.gif" height="11 src="> were linearly dependent, it is necessary that some vector be a linear combination of other vectors. 3) if some of the vectors from the system a1(vector), a2(vector)... ak(vector) are linearly dependent, then all vectors are linearly dependent. 4) if all vectors https://pandia.ru/text/78/365/images/image076_9.gif" height="11 src=">.gif" width="75" height="11"> https://pandia.ru/text/78/365/images/image082_10.gif" height="11 src=">.gif" height="11 src=">) Linear operations in coordinates. https://pandia.ru/text/78/365/images/image069_9.gif" height="12 src=">.gif" height="11 src=">.gif" height="11 src="> .gif" height="11 src=">+ (λa3)DIV_ADBLOCK413"> The scalar product of 2 vectors is a number equal to the product of the vectors and the cosine of the angle between them. https://pandia.ru/text/78/365/images/image090_8.gif" width="48" height="13"> 3. (a;b)=0, if and only if the vectors are orthoganal or some of the vectors is equal to 0. 4. Distributivity (αa+βb;c)=α(a;c)+β(b;c) 5. Expression of the scalar product of a and b in terms of their coordinates https://pandia.ru/text/78/365/images/image093_8.gif" width="40" height="11 src="> https://pandia.ru/text/78/365/images/image095_8.gif" width="254" height="13 src="> When condition () is met, h, l=1,2,3 https://pandia.ru/text/78/365/images/image098_7.gif" width="176" height="21 src="> https://pandia.ru/text/78/365/images/image065_9.gif" height="11"> and the third vector is called which satisfies the following equations: 3. – right Properties of a vector product: 4. Vector product of coordinate unit vectors Orthonormal basis. https://pandia.ru/text/78/365/images/image109_7.gif" width="41" height="11 src="> https://pandia.ru/text/78/365/images/image111_8.gif" width="41" height="11 src="> Often 3 symbols are used to denote unit vectors of an orthonormal basis https://pandia.ru/text/78/365/images/image063_10.gif" width="77" height="11 src="> https://pandia.ru/text/78/365/images/image114_5.gif" width="549" height="32 src="> If is an orthonormal basis, then DIV_ADBLOCK414"> Straight line on a plane. The relative position of 2 straight lines. Distance from a point to a straight line. The angle between two straight lines. The condition of parallelism and perpendicularity of 2 straight lines. 1. A special case of the arrangement of 2 straight lines on a plane. 1) - equation of a straight line parallel to the OX axis 2) - equation of a straight line parallel to the axis of the op-amp 2. Reciprocal arrangement of 2 straight lines. Theorem 1 Let the equations of straight lines be given with respect to an affine coordinate system A) Then the necessary and sufficient condition for when they intersect has the form: B) Then the necessary and sufficient condition for the fact that the lines are parallel is the condition: B) Then a necessary and sufficient condition for the fact that the lines merge into one is the condition: 3. Distance from a point to a line. Theorem. Distance from a point to a line relative to the Cartesian coordinate system: https://pandia.ru/text/78/365/images/image127_7.gif" width="34" height="11 src="> 4. Angle between two straight lines. Perpendicularity condition. Let 2 straight lines be defined relative to the Cartesian coordinate system by general equations. https://pandia.ru/text/78/365/images/image133_4.gif" width="103" height="11 src="> If , then the lines are perpendicular. Question 24. Plane in space. Condition for vector and plane to be consistent. Distance from a point to a plane. The condition of parallelism and perpendicularity of two planes. 1. Condition for the vector and the plane to be consistent. https://pandia.ru/text/78/365/images/image138_6.gif" width="40" height="11 src="> https://pandia.ru/text/78/365/images/image140.jpg" alt="Nameless4.jpg" width="111" height="39">!} https://pandia.ru/text/78/365/images/image142_6.gif" width="86" height="11 src="> https://pandia.ru/text/78/365/images/image144_6.gif" width="148" height="11 src="> https://pandia.ru/text/78/365/images/image145.jpg" alt="Nameless5.jpg" width="88" height="57">!} https://pandia.ru/text/78/365/images/image147_6.gif" width="31" height="11 src="> https://pandia.ru/text/78/365/images/image148_4.gif" width="328" height="24 src="> 3. Angle between 2 planes. Perpendicularity condition. https://pandia.ru/text/78/365/images/image150_6.gif" width="132" height="11 src="> If , then the planes are perpendicular. Question 25. Straight line in space. Different kinds equations of a straight line in space. https://pandia.ru/text/78/365/images/image156_6.gif" width="111" height="19"> 2. Vector equation of a line in space. https://pandia.ru/text/78/365/images/image138_6.gif" width="40" height="11 src="> https://pandia.ru/text/78/365/images/image162_5.gif" width="44" height="29 src="> 4. The canonical equation is direct. https://pandia.ru/text/78/365/images/image164_4.gif" width="34" height="18 src="> https://pandia.ru/text/78/365/images/image166_0.jpg" alt="Nameless3.jpg" width="56" height="51">
!} Question 28. Ellipse. Derivation of the Canonical Ellipse Equation. Form. Properties Ellipse is the locus of points for which the sum of distances from two fixed distances, called foci, is given number 2a, greater than the distance 2c between the foci. in Fig. 2 r1=a+ex r2=a-ex Ur-e tangent to the ellipse DIV_ADBLOCK417"> Canonical hyperbola equation Form and saints y=±b/a multiplied by the root of (x2-a2) Axis of symmetry of a hyperbola - its axes Segment 2a - real axis of the hyperbola Eccentricity e=2c/2a=c/a If b=a we get an isosceles hyperbola An asymptote is a straight line if, with an unlimited distance of point M1 along the curve, the distance from the point to the straight line tends to zero. lim d=0 at x-> ∞ d=ba2/(x1+(x21-a2)1/2/c) tangent of the hyperbola xx0/a2 - yy0/b2 = 1 parabola - a locus of points equidistant from a point called the focus and a given line called the directrix Canonical parabola equation properties the axis of symmetry of a parabola passes through its focus and is perpendicular to the directrix if you rotate a parabola you get an elliptical paraboloid all parabolas are similar question 30. Study of the equation of the general form of a second-order curve. Curve type def. with the leading terms A1, B1, C1 A1x12+2Bx1y1+C1y12+2D1x1+2E1y1+F1=0 1. AC=0 ->parabolic type curve A=C=0 => 2Dx+2Ey+F=0 A≠0 C=0 => Ax2+2Dx+2Ey+F=0 If E=0 => Ax2+2Dx+F=0 then x1=x2 - merges into one x1≠x2 - lines parallel to Оу x1≠x2 and the roots are imaginary, has no geometric image С≠0 А=0 =>C1y12+2D1x1+2E1y1+F1=0 Conclusion: a parabolic type curve is either a parabola, or 2 parallel lines, or imaginary, or merge into one. 2.AC>0 -> elliptic curve Complementing the original equation to a complete square, we transform it to the canonical one, then we get the cases (x-x0)2/a2+(y-y0)2/b2=1 - ellipse (x-x0)2/a2+(y-y0)2/b2=-1 - imaginary ellipse (x-x0)2/a2-(y-y0)2/b2=0 - point with coordinate x0 y0 Conclusion: e-curve. like this is either an ellipse, or an imaginary one, or a point 3. AC<0 - кривая гиперболического типа (x-x0)2/a2-(y-y0)2/b2=1 hyperbola, real axis parallel to Ox (x-x0)2/a2-(y-y0)2/b2=-1 hyperbola, real axis parallel to Oy (x-x0)2/a2-(y-y0)2/b2=0 level of two lines Conclusion: a hyperbolic curve is either a hyperbola or two straight lines A matrix is a special object in mathematics. It is depicted in the form of a rectangular or square table, composed of a certain number of rows and columns. In mathematics there is a wide variety of types of matrices, varying in size or content. The numbers of its rows and columns are called orders. These objects are used in mathematics to organize the recording of systems of linear equations and conveniently search for their results. Equations using a matrix are solved using the method of Carl Gauss, Gabriel Cramer, minors and algebraic additions, as well as many other methods. The basic skill when working with matrices is reduction to a standard form. However, first, let's figure out what types of matrices are distinguished by mathematicians. All components of this type of matrix are zeros. Meanwhile, the number of its rows and columns is completely different. The number of columns and rows of this type of matrix is the same. In other words, it is a “square” shaped table. The number of its columns (or rows) is called the order. Special cases are considered to be the existence of a second-order matrix (2x2 matrix), fourth-order (4x4), tenth-order (10x10), seventeenth-order (17x17) and so on. This is one of the simplest types of matrices, containing only one column, which includes three numerical values. It represents a number of free terms (numbers independent of variables) in systems of linear equations. View similar to the previous one. Consists of three numerical elements, in turn organized into one line. Numerical values in the diagonal form of the matrix take only the components of the main diagonal (highlighted in green). The main diagonal begins with the element in the upper right corner and ends with the number in the third column of the third row. The remaining components are equal to zero. The diagonal type is only a square matrix of some order. Among the diagonal matrices, one can distinguish the scalar one. All its components take the same values. A subtype of diagonal matrix. All its numerical values are units. Using a single type of matrix table, one performs its basic transformations or finds a matrix inverse to the original one. The canonical form of the matrix is considered one of the main ones; Reducing to it is often necessary for work. The number of rows and columns in a canonical matrix varies, and it does not necessarily belong to the square type. It is somewhat similar to the identity matrix, but in its case not all components of the main diagonal take on a value equal to one. There can be two or four main diagonal units (it all depends on the length and width of the matrix). Or there may be no units at all (then it is considered zero). The remaining components of the canonical type, as well as the diagonal and unit elements, are equal to zero. One of the most important types of matrix, used when searching for its determinant and when performing simple operations. The triangular type comes from the diagonal type, so the matrix is also square. The triangular type of matrix is divided into upper triangular and lower triangular. In an upper triangular matrix (Fig. 1), only elements that are above the main diagonal take a value equal to zero. The components of the diagonal itself and the part of the matrix located under it contain numerical values. In the lower triangular matrix (Fig. 2), on the contrary, the elements located in the lower part of the matrix are equal to zero. The type is necessary to find the rank of a matrix, as well as for elementary operations on them (along with the triangular type). The step matrix is so named because it contains characteristic "steps" of zeros (as shown in the figure). In the step type, a diagonal of zeros is formed (not necessarily the main one), and all elements under this diagonal also have values equal to zero. A prerequisite is the following: if there is a zero row in the step matrix, then the remaining rows below it also do not contain numerical values. Thus, we examined the most important types of matrices necessary to work with them. Now let's look at the problem of converting the matrix into the required form. How to bring a matrix to a triangular form? Most often in tasks you need to transform a matrix into a triangular form in order to find its determinant, otherwise called a determinant. When performing this procedure, it is extremely important to “preserve” the main diagonal of the matrix, because the determinant of a triangular matrix is equal to the product of the components of its main diagonal. Let me also recall alternative methods for finding the determinant. The determinant of the square type is found using special formulas. For example, you can use the triangle method. For other matrices, the method of decomposition by row, column or their elements is used. You can also use the method of minors and algebraic matrix additions. Let us analyze in detail the process of reducing a matrix to a triangular form using examples of some tasks. It is necessary to find the determinant of the presented matrix using the method of reducing it to triangular form. The matrix given to us is a third-order square matrix. Therefore, to transform it into a triangular shape, we will need to zero out two components of the first column and one component of the second. To bring it to triangular form, we start the transformation from the lower left corner of the matrix - from the number 6. To turn it to zero, multiply the first row by three and subtract it from the last row. Important! The top row does not change, but remains the same as in the original matrix. There is no need to write a string four times larger than the original one. But the values of the strings whose components need to be set to zero are constantly changing. Only the last value remains - the element of the third row of the second column. This is the number (-1). To turn it to zero, subtract the second from the first line. Let's check: detA = 2 x (-1) x 11 = -22. This means that the answer to the task is -22. It is necessary to find the determinant of the matrix by reducing it to triangular form. The presented matrix belongs to the square type and is a fourth-order matrix. This means that it is necessary to turn three components of the first column, two components of the second column and one component of the third to zero. Let's start reducing it with the element located in the lower left corner - with the number 4. We need to turn this number to zero. The easiest way to do this is to multiply the top line by four and then subtract it from the fourth. Let's write down the result of the first stage of transformation. So the fourth row component is set to zero. Let's move on to the first element of the third line, to the number 3. We perform a similar operation. We multiply the first line by three, subtract it from the third line and write down the result. We managed to turn to zero all the components of the first column of this square matrix, with the exception of the number 1 - an element of the main diagonal that does not require transformation. Now it is important to preserve the resulting zeros, so we will perform the transformations with rows, not with columns. Let's move on to the second column of the presented matrix. Let's start again at the bottom - with the element of the second column of the last row. This number is (-7). However, in this case it is more convenient to start with the number (-1) - the element of the second column of the third row. To turn it to zero, subtract the second from the third line. Then we multiply the second line by seven and subtract it from the fourth. We got zero instead of the element located in the fourth row of the second column. Now let's move on to the third column. In this column, we need to turn only one number to zero - 4. This is not difficult to do: we simply add a third to the last line and see the zero we need. After all the transformations made, we brought the proposed matrix to a triangular form. Now, to find its determinant, you only need to multiply the resulting elements of the main diagonal. We get: detA = 1 x (-1) x (-4) x 40 = 160. Therefore, the solution is 160. So, now the question of reducing the matrix to triangular form will not bother you. For elementary operations on matrices, the stepped form is less “in demand” than the triangular one. It is most often used to find the rank of a matrix (i.e., the number of its non-zero rows) or to determine linearly dependent and independent rows. However, the stepped type of matrix is more universal, as it is suitable not only for the square type, but also for all others. To reduce a matrix to stepwise form, you first need to find its determinant. The above methods are suitable for this. The purpose of finding the determinant is to find out whether it can be converted into a step matrix. If the determinant is greater or less than zero, then you can safely proceed to the task. If it is equal to zero, it will not be possible to reduce the matrix to a stepwise form. In this case, you need to check whether there are any errors in the recording or in the matrix transformations. If there are no such inaccuracies, the task cannot be solved. Let's look at how to reduce a matrix to a stepwise form using examples of several tasks. Exercise 1. Find the rank of the given matrix table. Before us is a third-order square matrix (3x3). We know that to find the rank it is necessary to reduce it to a stepwise form. Therefore, first we need to find the determinant of the matrix. Let's use the triangle method: detA = (1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) - (1 x 1 x 4) - (2 x 3 x 0) - (6 x 5 x 2) = 12. Determinant = 12. It is greater than zero, which means that the matrix can be reduced to a stepwise form. Let's start transforming it. Let's start it with the element of the left column of the third line - the number 2. Multiply the top line by two and subtract it from the third. Thanks to this operation, both the element we need and the number 4 - the element of the second column of the third row - turned to zero. We see that as a result of the reduction, a triangular matrix was formed. In our case, we cannot continue the transformation, since the remaining components cannot be reduced to zero. This means that we conclude that the number of rows containing numerical values in this matrix (or its rank) is 3. The answer to the task: 3. Task 2. Determine the number of linearly independent rows of this matrix. We need to find strings that cannot be converted to zero by any transformation. In fact, we need to find the number of non-zero rows, or the rank of the presented matrix. To do this, let us simplify it. We see a matrix that does not belong to the square type. It measures 3x4. Let's also start the reduction with the element of the lower left corner - the number (-1). Its further transformations are impossible. This means that we conclude that the number of linearly independent lines in it and the answer to the task is 3. Now reducing the matrix to a stepped form is not an impossible task for you. Using examples of these tasks, we examined the reduction of a matrix to a triangular form and a stepped form. To turn the desired values of matrix tables to zero, in some cases you need to use your imagination and correctly convert their columns or rows. Good luck in mathematics and in working with matrices! Matrix
dimension is a table of numbers containing rows and columns. The numbers are called the elements of this matrix, where is the row number, is the column number at the intersection of which this element stands. A matrix containing rows and columns has the form: Types of matrices: 1) at – square
, and they call matrix order
; 2) a square matrix in which all non-diagonal elements are equal to zero – diagonal
; 3) a diagonal matrix in which all diagonal elements are equal unit – single
and is denoted by ; 4) at – rectangular
; 5) when – row matrix (row vector); 6) when – matrix-column (vector-column); 7) for all – zero matrix. Note that the main numerical characteristic of a square matrix is its determinant. The determinant corresponding to a matrix of the th order also has the th order. Determinant of a 1st order matrix
called number. Determinant of a 2nd order matrix
called number Determinant of a 3rd order matrix
called number Let us present the definitions necessary for further presentation. Minor M
ij
element
A
ij
matrices n- order A is called the determinant of the matrix ( n-1)- th order obtained from matrix A by deleting i-th line and j th column. Algebraic complement A
ij
element
A
ij
matrices n-
of order A is the minor of this element, taken with the sign . Let us formulate the basic properties of determinants that are inherent in determinants of all orders and simplify their calculation. 1. When a matrix is transposed, its determinant does not change. 2. When rearranging two rows (columns) of a matrix, its determinant changes sign. 3. A determinant that has two proportional (equal) rows (columns) is equal to zero. 4. The common factor of the elements of any row (column) of the determinant can be taken out of the sign of the determinant. 5. If the elements of any row (column) of a determinant are the sum of two terms, then the determinant can be decomposed into the sum of two corresponding determinants. 6. The determinant will not change if the corresponding elements of its other row (column), previously multiplied by any number, are added to the elements of any of its rows (columns). 7. The determinant of a matrix is equal to the sum of the products of the elements of any of its rows (columns) by the algebraic complements of these elements. Let us explain this property using the example of a 3rd order determinant. In this case, property 7 means that Property 7 is a determinant decomposition theorem formulated by Laplace. 8. The sum of the products of the elements of any row (column) of a determinant by the algebraic complements of the corresponding elements of its other row (column) is equal to zero. The last property is often called pseudo-decomposition of the determinant. Self-test questions. 1. What is called a matrix? 2. Which matrix is called square? What is meant by its order? 3. What matrix is called diagonal, identity? 4. Which matrix is called a row matrix and a column matrix? 5. What is the main numerical characteristic of a square matrix? 6. What number is called the determinant of the 1st, 2nd and 3rd order? 7. What is called the minor and algebraic complement of a matrix element? 8. What are the main properties of determinants? 9. Using what property can one calculate the determinant of any order? Actions on matrices(scheme 2) A number of operations are defined on a set of matrices, the main ones being the following: 1) transposition
– replacing matrix rows with columns, and columns with rows; 2) multiplying a matrix by a number is done element-by-element, that is 3) matrix addition, defined only for matrices of the same dimension; 4) multiplication of two matrices, defined only for matched matrices. The sum (difference) of two matrices
such a resulting matrix is called, each element of which is equal to the sum (difference) of the corresponding elements of the matrix-commands. The two matrices are called agreed upon
, if the number of columns of the first one is equal to the number of rows of the other. Product of two matched matrices
and such a resulting matrix is called Where , . It follows that the element of the th row and the th column of the matrix is equal to the sum of pairwise products of the elements of the th row of the matrix and the elements of the th column of the matrix. The product of matrices is not commutative, that is, A .
B B .
A. An exception is, for example, the product of square matrices and unit A .
E = E .
A. Example 1.1. Multiply matrices A and B if: Solution. Since the matrices are consistent (the number of matrix columns is equal to the number of matrix rows), we will use formula (1.4): Self-test questions. 1. What actions are performed on matrices? 2. What is called the sum (difference) of two matrices? 3. What is called the product of two matrices? Cramer's method for solving quadratic systems of linear algebraic equations(scheme 3) Let us give a number of necessary definitions. The system of linear equations is called heterogeneous
, if at least one of its free terms is different from zero, and homogeneous
, if all its free terms are equal to zero. Solving a system of equations
is an ordered set of numbers that, when substituted for variables in a system, turns each of its equations into an identity. The system of equations is called joint
, if it has at least one solution, and non-joint
, if she has no solutions. The simultaneous system of equations is called certain
, if it has a unique solution, and uncertain
, if it has more than one solution. Let us consider an inhomogeneous quadratic system of linear algebraic equations having the following general form: The determinant of the main matrix of the system is called main determinant
and is designated . The auxiliary determinant is obtained from the main determinant by replacing the th column with a column of free terms. Theorem 1.1 (Cramer's theorem). If the main determinant of a quadratic system of linear algebraic equations is nonzero, then the system has a unique solution, calculated by the formulas: If the main determinant is , then the system either has an infinite number of solutions (for all zero auxiliary determinants) or has no solution at all (if at least one of the auxiliary determinants differs from zero) In light of the above definitions, Cramer's theorem can be formulated differently: if the main determinant of a system of linear algebraic equations is nonzero, then the system is jointly defined and at the same time ;
if the main determinant is zero, then the system is either jointly indefinite (for all ) or inconsistent (if at least one of them differs from zero). After this, the resulting solution should be checked. Example 1.2. Solve the system using Cramer's method Solution. Since the main determinant of the system Let's use Cramer's formulas (1.6): Self-test questions. 1. What is called solving a system of equations? 2. Which system of equations is called compatible or incompatible? 3. Which system of equations is called definite or indefinite? 4. Which matrix of the system of equations is called the main one? 5. How to calculate auxiliary determinants of a system of linear algebraic equations? 6. What is the essence of Cramer’s method for solving systems of linear algebraic equations? 7. What can a system of linear algebraic equations be like if its main determinant is zero? Solving quadratic systems of linear algebraic equations using the inverse matrix method(scheme 4) A matrix having a nonzero determinant is called non-degenerate
; having a determinant equal to zero – degenerate
. The matrix is called the inverse
for a given square matrix, if when multiplying the matrix by its inverse both on the right and on the left, the identity matrix is obtained, that is. (1.7)
Note that in this case the product of matrices and is commutative. Theorem 1.2. A necessary and sufficient condition for the existence of an inverse matrix for a given square matrix is that the determinant of the given matrix is different from zero If the main matrix of the system turns out to be singular during testing, then there is no inverse for it, and the method under consideration cannot be applied. If the main matrix is non-singular, that is, the determinant is 0, then the inverse matrix can be found for it using the following algorithm. 1. Calculate the algebraic complements of all matrix elements. 2. Write the found algebraic additions into the matrix transposed. 3. Create an inverse matrix using the formula: 4. Check the correctness of the found matrix A-1 according to formula (1.7). Note that this check can be included in the final check of the system solution itself. System (1.5) of linear algebraic equations can be represented as a matrix equation: , where is the main matrix of the system, is the column of unknowns, and is the column of free terms. Let's multiply this equation on the left by the inverse matrix, we get: Since, by definition of the inverse matrix, the equation takes the form Thus, to solve a quadratic system of linear algebraic equations, you need to multiply the column of free terms on the left by the matrix inverse of the main matrix of the system. After this, you should check the resulting solution. Example 1.3. Solve the system using the inverse matrix method Solution. Let us calculate the main determinant of the system Let's find the algebraic complements of all elements of the main matrix: Let us write the algebraic additions transposed into the matrix Self-test questions. 1. Which matrix is called singular, non-degenerate? 2. What matrix is called the inverse of a given one? What is the condition of its existence? 3. What is the algorithm for finding the inverse matrix for a given one? 4. What matrix equation is equivalent to a system of linear algebraic equations? 5. How to solve a system of linear algebraic equations using the inverse matrix for the main matrix of the system? Study of inhomogeneous systems of linear algebraic equations(scheme 5) The study of any system of linear algebraic equations begins with the transformation of its extended matrix by the Gaussian method. Let the dimension of the main matrix of the system be equal to . Matrix
called extended
matrix of the system ,
if, along with the coefficients of the unknowns, it contains a column of free terms. Therefore, the dimension is . The Gaussian method is based on elementary transformations
, which include: – rearrangement of matrix rows; – multiplying the rows of the matrix by a number different from the steering wheel; – element-wise addition of matrix rows; – deleting the zero line; – matrix transposition (in this case, transformations are carried out by columns). Elementary transformations lead the original system to a system equivalent to it. Systems are called equivalent
, if they have the same set of solutions. Matrix rank
is called the highest order of its nonzero minors. Elementary transformations do not change the rank of the matrix. The following theorem answers the question about the existence of solutions for an inhomogeneous system of linear equations. Theorem 1.3 (Kronecker-Capelli theorem). A non-homogeneous system of linear algebraic equations is consistent if and only if the rank of the extended matrix of the system is equal to the rank of its main matrix, i.e. Let us denote the number of rows remaining in the matrix after the Gaussian method by (accordingly, the number of equations remaining in the system). These lines
matrices are called basic
. If , then the system has a unique solution (is jointly defined), its matrix is reduced to a triangular form by elementary transformations. Such a system can be solved using the Cramer method, using the inverse matrix, or the universal Gauss method. If (the number of variables in the system is greater than equations), the matrix is reduced to a stepwise form by elementary transformations. Such a system has many solutions and is jointly uncertain. In this case, to find solutions to the system, it is necessary to perform a number of operations. 1. Leave the system of unknowns on the left sides of the equations ( basic variables
), the rest of the unknowns are moved to the right sides ( free variables
). After dividing the variables into basic and free, the system takes the form: 2. From the coefficients of the basic variables, make up a minor ( basic minor
), which must be non-zero. 3. If the basic minor of system (1.10) is equal to zero, then replace one of the basic variables with a free one; Check the resulting basis minor for non-zero. 4. Applying formulas (1.6) of the Cramer method, considering the right-hand sides of the equations to be their free terms, find an expression for the basic variables in terms of the free ones in general form. The resulting ordered set of system variables is its general decision
. 5. Giving the free variables in (1.10) arbitrary values, calculate the corresponding values of the basic variables. The resulting ordered set of values of all variables is called private solution
systems corresponding to given values of free variables. The system has an infinite number of particular solutions. 6. Get basic solution
system – a particular solution obtained for zero values of free variables. Note that the number of basis sets of variables of system (1.10) is equal to the number of combinations of elements by elements. Since each basic set of variables has its own basic solution, therefore, the system also has basic solutions. A homogeneous system of equations is always consistent, since it has at least one – zero (trivial) solution. In order for a homogeneous system of linear equations with variables to have non-zero solutions, it is necessary and sufficient that its main determinant be equal to zero. This means that the rank of its main matrix is less than the number of unknowns. In this case, the study of a homogeneous system of equations for general and particular solutions is carried out similarly to the study of a non-homogeneous system. Solutions to a homogeneous system of equations have an important property: if two different solutions to a homogeneous system of linear equations are known, then their linear combination is also a solution to this system. It is easy to verify the validity of the following theorem. Theorem 1.4. The general solution of an inhomogeneous system of equations is the sum of the general solution of the corresponding homogeneous system and some particular solution of the inhomogeneous system of equations Example 1.4. Explore the given system and find one particular solution: Solution. Let us write down the extended matrix of the system and apply elementary transformations to it: According to formulas (1.6) we have For specific values of free variables, from the general solution we obtain a particular solution of the system. For example, a private solution Self-test questions. 1. Which system of equations is called homogeneous or inhomogeneous? 2. Which matrix is called extended? 3. List the basic elementary transformations of matrices. What method of solving systems of linear equations is based on these transformations? 4. What is the rank of a matrix? How can you calculate it? 5. What does the Kronecker-Capelli theorem say? 6. To what form can a system of linear algebraic equations be reduced as a result of its solution by the Gauss method? What does this mean? 7. Which rows of the matrix are called basic? 8. Which system variables are called basic and which are free? 9. What solution of an inhomogeneous system is called private? 10.Which of its solutions is called basic? How many basic solutions does an inhomogeneous system of linear equations have? 11.Which solution of an inhomogeneous system of linear algebraic equations is called general? Formulate a theorem about the general solution of an inhomogeneous system of equations. 12. What are the main properties of solutions to a homogeneous system of linear algebraic equations? DEFINITION OF MATRIX. TYPES OF MATRICES Matrix of size m× n called a set m·n numbers arranged in a rectangular table of m lines and n columns. This table is usually enclosed in parentheses. For example, the matrix might look like: For brevity, a matrix can be denoted by a single capital letter, for example, A or IN. In general, a matrix of size m× n write it like this The numbers that make up the matrix are called matrix elements. It is convenient to provide matrix elements with two indices a ij: The first indicates the row number and the second indicates the column number. For example, a 23– the element is in the 2nd row, 3rd column. If a matrix has the same number of rows as the number of columns, then the matrix is called square, and the number of its rows or columns is called in order matrices. In the above examples, the second matrix is square - its order is 3, and the fourth matrix is its order 1. A matrix in which the number of rows is not equal to the number of columns is called rectangular. In the examples this is the first matrix and the third. There are also matrices that have only one row or one column. A matrix with only one row is called matrix - row(or string), and a matrix with only one column matrix - column. A matrix whose elements are all zero is called null and is denoted by (0), or simply 0. For example, Main diagonal of a square matrix we call the diagonal going from the upper left to the lower right corner. A square matrix in which all elements below the main diagonal are equal to zero is called triangular matrix. A square matrix in which all elements, except perhaps those on the main diagonal, are equal to zero, is called diagonal matrix. For example, or. A diagonal matrix in which all diagonal elements are equal to one is called single matrix and is denoted by the letter E. For example, the 3rd order identity matrix has the form ACTIONS ON MATRICES Matrix equality. Two matrices A And B are said to be equal if they have the same number of rows and columns and their corresponding elements are equal a ij = b ij. So if Transpose. Consider an arbitrary matrix A from m lines and n columns. It can be associated with the following matrix B from n lines and m columns, in which each row is a matrix column A with the same number (hence each column is a row of the matrix A with the same number). So if This matrix B called transposed matrix A, and the transition from A To B transposition. Thus, transposition is a reversal of the roles of the rows and columns of a matrix. Matrix transposed to matrix A, usually denoted A T. Communication between matrix A and its transpose can be written in the form . For example. Find the matrix transposed of the given one. Matrix addition. Let the matrices A And B consist of the same number of rows and the same number of columns, i.e. have same sizes. Then in order to add matrices A And B needed for matrix elements A add matrix elements B standing in the same places. Thus, the sum of two matrices A And B called a matrix C, which is determined by the rule, for example, Examples. Find the sum of matrices: It is easy to verify that matrix addition obeys the following laws: commutative A+B=B+A and associative ( A+B)+C=A+(B+C). Multiplying a matrix by a number. To multiply a matrix A per number k every element of the matrix is needed A multiply by this number. Thus, the matrix product A per number k there is a new matrix, which is determined by the rule For any numbers a And b and matrices A And B the following equalities hold: Examples. Matrix multiplication. This operation is carried out according to a peculiar law. First of all, we note that the sizes of the factor matrices must be consistent. You can multiply only those matrices in which the number of columns of the first matrix coincides with the number of rows of the second matrix (i.e., the length of the first row is equal to the height of the second column). The work matrices A not a matrix B called the new matrix C=AB, the elements of which are composed as follows: Thus, for example, to obtain the product (i.e. in the matrix C) element located in the 1st row and 3rd column from 13, you need to take the 1st row in the 1st matrix, the 3rd column in the 2nd, and then multiply the row elements by the corresponding column elements and add the resulting products. And other elements of the product matrix are obtained using a similar product of the rows of the first matrix and the columns of the second matrix. In general, if we multiply a matrix A = (a ij) size m× n to the matrix B = (b ij) size n× p, then we get the matrix C size m× p, whose elements are calculated as follows: element c ij is obtained as a result of the product of elements i th row of the matrix A to the corresponding elements j th matrix column B and their additions. From this rule it follows that you can always multiply two square matrices of the same order, and as a result we obtain a square matrix of the same order. In particular, a square matrix can always be multiplied by itself, i.e. square it. Another important case is the multiplication of a row matrix by a column matrix, and the width of the first must be equal to the height of the second, resulting in a first-order matrix (i.e. one element). Really, Examples. Thus, these simple examples show that matrices, generally speaking, do not commute with each other, i.e. A∙B ≠ B∙A
. Therefore, when multiplying matrices, you need to carefully monitor the order of the factors. It can be verified that matrix multiplication obeys associative and distributive laws, i.e. (AB)C=A(BC) And (A+B)C=AC+BC. It is also easy to check that when multiplying a square matrix A to the identity matrix E of the same order we again obtain a matrix A, and AE=EA=A. The following interesting fact can be noted. As you know, the product of 2 non-zero numbers is not equal to 0. For matrices this may not be the case, i.e. the product of 2 non-zero matrices may turn out to be equal to the zero matrix. For example, If THE CONCEPT OF DETERMINANTS Let a second-order matrix be given - a square matrix consisting of two rows and two columns Second order determinant corresponding to a given matrix is the number obtained as follows: a 11 a 22 – a 12 a 21. The determinant is indicated by the symbol So, in order to find the second-order determinant, you need to subtract the product of the elements along the second diagonal from the product of the elements of the main diagonal. Examples. Calculate second order determinants. Similarly, we can consider a third-order matrix and its corresponding determinant. Third order determinant, corresponding to a given square matrix of third order, is the number denoted and obtained as follows: Thus, this formula gives the expansion of the third-order determinant in terms of the elements of the first row a 11, a 12, a 13 and reduces the calculation of the third-order determinant to the calculation of the second-order determinants. Examples. Calculate the third order determinant. Similarly, one can introduce the concepts of determinants of the fourth, fifth, etc. orders, lowering their order by expanding into the elements of the 1st row, with the “+” and “–” signs of the terms alternating. So, unlike a matrix, which is a table of numbers, a determinant is a number that is assigned to the matrix in a certain way. Operations on matrices and their properties. The concept of a determinant of the second and third orders.Properties of determinants and their calculation. 3. General description of the task. 4. Completing tasks. 5. Preparation of a report on laboratory work. Glossary Learn the definitions of the following terms: Dimension A matrix is a collection of two numbers, consisting of the number of its rows m and the number of columns n. If m=n, then the matrix is called square matrix of order n. Operations on matrices: transposing a matrix, multiplying (dividing) a matrix by a number, adding and subtracting, multiplying a matrix by a matrix. The transition from a matrix A to a matrix A m, the rows of which are the columns, and the columns are the rows of the matrix A, is called transposition matrices A. Example: A = , A t = . To multiply matrix by number, you need to multiply each element of the matrix by this number. Example: 2A= 2· = . Sum (difference) matrices A and B of the same dimension are called matrix C=A B, the elements of which are equal with ij = a ij b ij for all i And j. Example: A = ; B = . A+B= The work matrix A m n by matrix B n k is called a matrix C m k , each element of which c ij is equal to the sum of the products of the elements of the i-th row of matrix A by the corresponding element of the j-th column of matrix B: c ij = a i1 · b 1j + a i2 ·b 2j +…+ a in ·b nj . To be able to multiply a matrix by a matrix, they must be agreed upon for multiplication, namely number of columns in the first matrix should be equal to number of lines in the second matrix. Example: A= and B=. А·В—impossible, because they are not consistent. VA= . = Properties of the matrix multiplication operation. 1. If matrix A has the dimension m n, and matrix B is the dimension n k, then the product A·B exists. The product BA can exist only when m=k. 2. Matrix multiplication is not commutative, i.e. A·B is not always equal to BA·A even if both products are defined. However, if the relation А·В=В·А is satisfied, then the matrices A and B are called permutable. Example. Calculate. Minor element is the determinant of the order matrix, obtained by deleting the th row of the th column. Algebraic complement element is called . Laplace expansion theorem: The determinant of a square matrix is equal to the sum of the products of the elements of any row (column) by their algebraic complements. Example. Calculate. Solution. . Properties of nth order determinants: 1) The value of the determinant will not change if the rows and columns are swapped. 2) If the determinant contains a row (column) of only zeros, then it is equal to zero. 3) When rearranging two rows (columns), the determinant changes sign. 4) A determinant that has two identical rows (columns) is equal to zero. 5) The common factor of the elements of any row (column) can be taken out of the determinant sign. 6) If each element of a certain row (column) is the sum of two terms, then the determinant is equal to the sum of two determinants, in each of which all rows (columns), except the one mentioned, are the same as in this determinant, and in the mentioned row ( Column) of the first determinant contains the first terms, the second - the second. 7) If two rows (columns) in the determinant are proportional, then it is equal to zero. 8) The determinant will not change if the corresponding elements of another row (column) are added to the elements of a certain row (column), multiplied by the same number. 9) The determinants of triangular and diagonal matrices are equal to the product of the elements of the main diagonal. The method of accumulating zeros for calculating determinants is based on the properties of determinants. Example. Calculate. Solution. Subtract the double third from the first row, then use the expansion theorem in the first column. ~ Control questions(OK-1, OK-2, OK-11, PK-1) :
1. What is called a second-order determinant? 2. What are the main properties of determinants? 3. What is the minor of an element? 4. What is called the algebraic complement of an element of a determinant? 5. How to expand the third-order determinant into elements of a row (column)? 6. What is the sum of the products of the elements of a row (or column), the determinant of the algebraic complements of the corresponding elements of another row (or column)? 7. What is the rule of triangles? 8. How are determinants of higher orders calculated using the order reduction method? 10. Which matrix is called square? Null? What is a row matrix, column matrix? 11. Which matrices are called equal? 12. Give definitions of the operations of addition, multiplication of matrices, multiplication of a matrix by a number 13. What conditions must the sizes of matrices satisfy during addition and multiplication? 14. What are the properties of algebraic operations: commutativity, associativity, distributivity? Which of them are fulfilled for matrices during addition and multiplication, and which are not? 15. What is an inverse matrix? For what matrices is it defined? 16. Formulate a theorem on the existence and uniqueness of the inverse matrix. 17.
Formulate a lemma on the transposition of a product of matrices. General practical tasks(OK-1, OK-2, OK-11, PK-1) :
No. 1. Find the sum and difference of matrices A and B :
A) b) V) No. 2. Follow these steps :
c) Z= -11A+7B-4C+D If No. 3. Follow these steps :
V) No. 4. Using four methods of calculating the determinant of a square matrix, find the determinants of the following matrices :
No. 5. Find determinants of the nth order, based on the elements of the column (row) :
A) No. 6. Find the determinant of a matrix using the properties of determinants: A) 
![]()

![]()
![]()
 https://pandia.ru/text/78/365/images/image195_4.gif" alt="image002" width="17" height="23 id=">.gif" alt="image043" width="81 height=44" height="44"> 0=!}
https://pandia.ru/text/78/365/images/image195_4.gif" alt="image002" width="17" height="23 id=">.gif" alt="image043" width="81 height=44" height="44"> 0=!} 

Null type
Square type

Column vector


Diagonal type



Canonical type

Triangular type


Reducing to triangular form
Exercise 1

Task 2

Reducing to a stepped form


 .
. . (1.1)
. (1.1)
 . (1.2)
. (1.2)
 – decomposition of the determinant into elements of the 1st row. Note that for the decomposition, select the row (column) where there are zero elements, since the corresponding terms in the decomposition turn to zero.
– decomposition of the determinant into elements of the 1st row. Note that for the decomposition, select the row (column) where there are zero elements, since the corresponding terms in the decomposition turn to zero.![]() , Where ,
;
, Where ,
;![]() , What , (1.4)
, What , (1.4)

 .
.
 . (1.5) The main matrix of the system
linear algebraic equations is a matrix composed of coefficients associated with the unknowns:
. (1.5) The main matrix of the system
linear algebraic equations is a matrix composed of coefficients associated with the unknowns:  .
.
 is different from zero, then the system has a unique solution. Let's calculate auxiliary determinants
is different from zero, then the system has a unique solution. Let's calculate auxiliary determinants
 , ,
, ,  (1.8)
(1.8)
![]() or . (1.9)
or . (1.9)

 . Consequently, the matrix is non-singular and its inverse matrix exists.
. Consequently, the matrix is non-singular and its inverse matrix exists.


 . Let us use formulas (1.8) and (1.9) to find a solution to the system
. Let us use formulas (1.8) and (1.9) to find a solution to the system![]()
 . (1.10)
. (1.10)



 . Since and , then by Theorem 1.3 (Kronecker-Capelli) the given system of linear algebraic equations is consistent. The number of variables, i.e., means the system is uncertain. The number of basis sets of system variables is equal to
. Since and , then by Theorem 1.3 (Kronecker-Capelli) the given system of linear algebraic equations is consistent. The number of variables, i.e., means the system is uncertain. The number of basis sets of system variables is equal to . Consequently, 6 sets of variables can be basic: . Let's consider one of them. Then the system obtained as a result of the Gauss method can be rewritten in the form
. Consequently, 6 sets of variables can be basic: . Let's consider one of them. Then the system obtained as a result of the Gauss method can be rewritten in the form . Main determinant
. Main determinant  . Using Cramer's method, we look for a general solution to the system. Auxiliary qualifiers
. Using Cramer's method, we look for a general solution to the system. Auxiliary qualifiers
 . This expression of basic variables in terms of free ones represents the general solution of the system:
. This expression of basic variables in terms of free ones represents the general solution of the system: corresponds to the values of free variables
corresponds to the values of free variables ![]() . At we obtain the basic solution of the system
. At we obtain the basic solution of the system 
 .
. .
. .
. .
. And
And  , That A=B, If a 11 = b 11, a 12 = b 12, a 21 = b 21 And a 22 = b 22.
, That A=B, If a 11 = b 11, a 12 = b 12, a 21 = b 21 And a 22 = b 22. , That
, That  .
.
![]()

 or .
or .![]()

 .
.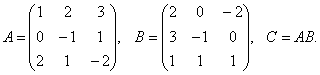
 , That
, That![]() .
. .
. .
.![]()
 .
.
![]() = .
= .![]() =
= ![]() .
.
![]()
![]()
 .
.




 b)
b) 
 b)
b) 


