Paralelkenar kavramı
Tanım 1
Paralelkenar karşıt kenarların birbirine paralel olduğu bir dörtgendir (Şekil 1).
Resim 1.
Paralelkenarın iki temel özelliği vardır. Bunları kanıt olmadan ele alalım.
Özellik 1: Paralelkenarın karşılıklı kenarları ve açıları sırasıyla eşittir.
Özellik 2: Paralelkenarda çizilen köşegenler kesişme noktalarına göre ikiye bölünür.
Paralelkenarın işaretleri
Bir paralelkenarın üç özelliğini ele alalım ve bunları teoremler şeklinde sunalım.
Teorem 1
Bir dörtgenin iki kenarı birbirine eşit ve paralel ise bu dörtgen bir paralelkenar olacaktır.
Kanıt.
Bize $ABCD$ dörtgeni verilsin. Burada $AB||CD$ ve $AB=CD$ içine çapraz bir $AC$ çizelim (Şekil 2).

Şekil 2.
$AB$ ve $CD$ paralel çizgilerini ve bunların sekantını $AC$ olarak düşünün. Daha sonra
\[\açı CAB=\açı DCA\]
çapraz köşeler gibi.
Üçgenlerin eşitliği $I$ kriterine göre,
$AC$ onların ortak tarafı olduğundan ve koşula göre $AB=CD$ olduğundan. Araç
\[\açı DAC=\açı ACB\]
$AD$ ve $CB$ doğrularını ve bunların kesenleri $AC$'ı düşünün; yatay açılar arasındaki son eşitlikten şunu elde ederiz: $AD||CB$.) Sonuç olarak, $1$ tanımı gereği bu dörtgen bir paralelkenardır.
Teorem kanıtlandı.
Teorem 2
Bir dörtgenin karşılıklı kenarları birbirine eşitse bu bir paralelkenardır.
Kanıt.
Bize $ABCD$ dörtgeni verilsin. Burada $AD=BC$ ve $AB=CD$. İçine çapraz bir $AC$ çizelim (Şekil 3).

Figür 3.
$AD=BC$, $AB=CD$ ve $AC$ ortak bir kenar olduğundan, üçgenlerin eşitliği için $III$ kriterine göre,
\[\üçgen DAC=\üçgen ACB\]
\[\açı DAC=\açı ACB\]
$AD$ ve $CB$ doğrularını ve bunların sekantını $AC$ ele alalım; yatış açıları arasındaki son eşitlikle $AD||CB$ değerini elde ederiz. Dolayısıyla $1$ tanımı gereği bu dörtgen bir paralelkenardır.
\[\açı DCA=\açı CAB\]
$AB$ ve $CD$ doğrularını ve bunların sekantını $AC$ ele alalım; yatış açıları arasındaki son eşitlikle $AB||CD$ değerini elde ederiz. Dolayısıyla Tanım 1'e göre bu dörtgen bir paralelkenardır.
Teorem kanıtlandı.
Teorem 3
Bir dörtgende çizilen köşegenler kesişme noktalarına göre iki eşit parçaya bölünürse bu dörtgen bir paralelkenardır.
Kanıt.
Bize $ABCD$ dörtgeni verilsin. İçine $AC$ ve $BD$ köşegenlerini çizelim. $O$ noktasında kesişmelerine izin verin (Şekil 4).
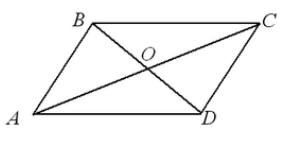
Şekil 4.
Koşul gereği $BO=OD,\ AO=OC$ ve $\angle COB=\angle DOA$ açıları dikey olduğundan, üçgenlerin eşitliği için $I$ kriterine göre,
\[\üçgen BOC=\üçgen AOD\]
\[\açı DBC=\açı BDA\]
$BC$ ve $AD$ doğrularını ve bunların sekantını $BD$ göz önünde bulundurun; yatış açıları arasındaki son eşitliğe göre $BC||AD$ değerini elde ederiz. Ayrıca $BC=AD$. Dolayısıyla $1$ Teoremine göre bu dörtgen bir paralelkenardır.
Paralelkenar, karşıt kenarları paralel olan bir dörtgendir, yani. paralel çizgiler üzerinde uzanmak
Paralelkenarın özellikleri:  Teorem 22.
Paralelkenarın karşılıklı kenarları eşittir.
Teorem 22.
Paralelkenarın karşılıklı kenarları eşittir.
Kanıt. ABCD paralelkenarında bir AC köşegeni çiziyoruz. ACD ve ACB üçgenleri, ortak bir AC kenarına ve iki çifte sahip olduklarından eşittir. eşit açılar. ona bitişik: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (AD ve BC paralel çizgileriyle çapraz açılar olarak). Bu, eşit üçgenlerin karşılık gelen kenarları olarak AB = CD ve BC = AD anlamına gelir. Bu üçgenlerin eşitliğinden üçgenlerin karşılık gelen açılarının da eşit olduğu sonucu çıkar:
Teorem 23.
Paralelkenarın zıt açıları eşittir: ∠ A=∠ C ve ∠ B=∠ D.
İlk çiftin eşitliği ABD ve CBD üçgenlerinin, ikincisi ise ABC ve ACD üçgenlerinin eşitliğinden gelir.
Teorem 24.
Bir paralelkenarın bitişik açıları, yani. bir tarafa bitişik açıların toplamı 180 dereceye kadar çıkar.
Bunun nedeni iç açıların tek taraflı olmasıdır.
Teorem 25.
Paralelkenarın köşegenleri kesişme noktalarında birbirini ortalar.
Kanıt. BOC ve AOD üçgenlerini düşünün. Birinci özelliğe göre AD=BC ∠ OAD=∠ OCB ve ∠ ODA=∠ OBC paralel AD ve BC doğruları için çapraz uzanır. Bu nedenle BOC ve AOD üçgenlerinin yan ve komşu açıları eşittir. Bu, eşit üçgenlerin karşılık gelen kenarları gibi BO=OD ve AO=OS anlamına gelir.
Paralelkenarın işaretleri
Teorem 26.
Bir dörtgenin karşılıklı kenarları çiftler halinde eşitse bu bir paralelkenardır.
Kanıt. ABCD dörtgeninin sırasıyla AD ve BC, AB ve CD kenarları eşit olsun (Şekil 2). AC köşegenini çizelim. ABC ve ACD üçgenlerinin üç tarafı eşittir. Bu durumda BAC ve DCA açıları eşittir ve bu nedenle AB, CD'ye paraleldir. BC ve AD kenarlarının paralelliği CAD ve ACB açılarının eşitliğinden kaynaklanır.
Teorem 27.
Bir dörtgenin zıt açıları çiftler halinde eşitse bu bir paralelkenardır.
∠ A=∠ C ve ∠ B=∠ D olsun. Çünkü ∠ A+∠ B+∠ C+∠ D=360 o ise ∠ A+∠ B=180 o ve AD ile BC kenarları paraleldir (düz çizgilerin paralelliğine göre). Ayrıca AB ve CD kenarlarının paralelliğini kanıtlayacağız ve ABCD'nin tanımı gereği bir paralelkenar olduğu sonucuna varacağız.
Teorem 28.
Bir dörtgenin bitişik köşeleri varsa, yani. Bir tarafa bitişik açıların toplamı 180 dereceye ulaşır, bu bir paralelkenardır.
Eğer iç tek taraflı açıların toplamı 180 derece ise düz çizgiler paraleldir. Yani AB, CD'ye paraleldir ve BC, AD'ye paraleldir. Bir dörtgenin tanımı gereği bir paralelkenar olduğu ortaya çıkıyor.
Teorem 29.
Bir dörtgenin köşegenleri kesişme noktasında birbirini ortalıyorsa bu dörtgen bir paralelkenardır.
Kanıt. Eğer AO = OC, BO = OD ise, AOD ve BOC üçgenleri eşittir, çünkü O köşesinde eşit (dikey) açılar vardır ve eşit kenar çiftleri arasında yer alır. Üçgenlerin eşitliğinden AD ve BC'nin eşit olduğu sonucunu çıkarıyoruz. AB ve CD kenarları da eşittir ve dörtgen, kriter 1'e göre bir paralelkenar olarak ortaya çıkar.
Teorem 30.
Bir dörtgenin bir çift eşit, paralel kenarı varsa, bu bir paralelkenardır.
ABCD dörtgeninin AB ve CD kenarları paralel ve eşit olsun. AC ve BD köşegenlerini çizelim. Bu çizgilerin paralelliğinden ABO = CDO ve BAO = OCD çapraz açılarının eşit olduğu sonucu çıkar. ABO ve CDO üçgenlerinin yan ve komşu açıları eşittir. Bu nedenle AO=OS, VO=ОD, yani. Köşegenler kesişme noktasına göre ikiye bölünür ve dörtgen, kriter 4'e göre bir paralelkenar olarak ortaya çıkar.
Geometride paralelkenarın özel durumları dikkate alınır.
Bu konuyla ilgili problemleri çözerken, Temel özellikler paralelkenar ve karşılık gelen formüller için aşağıdakileri hatırlayabilir ve uygulayabilirsiniz:
- Paralelkenarın bir iç açısının açıortayı, bu açıdan bir ikizkenar üçgeni keser
- Paralelkenarın kenarlarından birine bitişik iç açıların açıortayları karşılıklı olarak diktir
- Paralelkenarın karşılıklı iç köşelerinden gelen açıortaylar birbirine paraleldir veya aynı doğru üzerinde yer alır.
- Paralelkenarın köşegenlerinin karelerinin toplamı, kenarlarının karelerinin toplamına eşittir
- Paralelkenarın alanı köşegenlerin çarpımının yarısına ve aralarındaki açının sinüsüne eşittir
Bu özelliklerin kullanıldığı problemleri ele alalım.
Görev 1.
ABCD paralelkenarının C açısının açıortayı, AD kenarını M noktasında ve AB kenarının A noktasının ötesindeki devamını E noktasında keser. AE = 4, DM = 3 ise paralelkenarın çevresini bulun.
Çözüm.
1. Üçgen CMD ikizkenardır. (Özellik 1). Bu nedenle CD = MD = 3 cm'dir.
2. EAM Üçgeni ikizkenardır.
Bu nedenle AE = AM = 4 cm'dir.
3. AD = AM + MD = 7 cm.
4. Çevre ABCD = 20 cm.
Cevap. 20 santimetre.
Görev 2.
Köşegenler dışbükey bir ABCD dörtgeninde çizilmiştir. ABD, ACD, BCD üçgenlerinin alanlarının eşit olduğu bilinmektedir. Bu dörtgenin bir paralelkenar olduğunu kanıtlayın.

Çözüm.
1. BE ABD üçgeninin yüksekliği, CF ACD üçgeninin yüksekliği olsun. Problemin koşullarına göre üçgenlerin alanları eşit olduğundan ve ortak AD tabanına sahip olduklarından bu üçgenlerin yükseklikleri eşittir. BE = CF.
2. BE, CF AD'ye diktir. B ve C noktaları AD düz çizgisine göre aynı tarafta bulunur. BE = CF. Bu nedenle BC düz çizgisi || MS. (*)
3. AL, ACD üçgeninin yüksekliği, BK ise BCD üçgeninin yüksekliği olsun. Problemin koşullarına göre üçgenlerin alanları eşit olduğundan ve ortak CD tabanına sahip olduklarından bu üçgenlerin yükseklikleri de eşittir. AL = BK.
4. AL ve BK CD'ye diktir. B ve A noktaları CD düz çizgisine göre aynı tarafta bulunur. AL = BK. Bu nedenle AB düz çizgisi || CD (**)
5. (*), (**) koşullarından ABCD'nin bir paralelkenar olduğu sonucu çıkar.
Cevap. Kanıtlanmış. ABCD bir paralelkenardır.
Görev 3.
ABCD paralelkenarının BC ve CD kenarlarında sırasıyla M ve H noktaları işaretlenir, böylece BM ve HD parçaları O noktasında kesişir;<ВМD = 95 о,
 Çözüm.
Çözüm.
1. DOM üçgeninde<МОD = 25 о (Он смежный с <ВОD = 155 о); <ОМD = 95 о. Тогда <ОDМ = 60 о.
2. Bir dik üçgende DHC Daha sonra<НСD = 30 о. СD: НD = 2: 1 Ama CD = AB. O halde AB: HD = 2:1. 3. <С = 30 о, 4. <А = <С = 30 о, <В = Cevap: AB: HD = 2:1,<А = <С = 30 о, <В = Görev 4. Uzunluğu 4√6 olan bir paralelkenarın köşegenlerinden biri tabanla 60°, ikinci köşegen ise aynı tabanla 45° açı yapar. İkinci köşegeni bulun. Çözüm.
1.AO = 2√6. 2. Sinüs teoremini AOD üçgenine uyguluyoruz. AO/sin D = OD/sin A. 2√6/sin 45 o = OD/sin 60 o. ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6. Cevap: 12.
Görev 5. Kenarları 5√2 ve 7√2 olan bir paralelkenar için köşegenler arasındaki küçük açı, paralelkenarın küçük açısına eşittir. Köşegenlerin uzunluklarının toplamını bulun. Çözüm.
Paralelkenarın köşegenleri d 1, d 2 olsun ve köşegenler ile paralelkenarın küçük açısı arasındaki açı φ'ye eşit olsun. 1. İki farklı sayalım S ABCD = AB AD sin A = 5√2 7√2 sin f, S ABCD = 1/2 AC ВD sin AOB = 1/2 d 1 d 2 sin f. 5√2 · 7√2 · sin f = 1/2d 1 d 2 sin f veya eşitliğini elde ederiz. 2 · 5√2 · 7√2 = d1d2; 2. Paralelkenarın kenarları ve köşegenleri arasındaki ilişkiyi kullanarak eşitliği yazıyoruz (AB 2 + AD 2) 2 = AC 2 + BD 2. ((5√2) 2 + (7√2) 2) 2 = d 1 2 + d 2 2. d 1 2 + d 2 2 = 296. 3. Bir sistem oluşturalım: (d 1 2 + d 2 2 = 296, Sistemin ikinci denklemini 2 ile çarpıp birinciye ekleyelim. (d 1 + d 2) 2 = 576 elde ederiz. Dolayısıyla Id 1 + d 2 I = 24. d 1, d 2 paralelkenarın köşegenlerinin uzunlukları olduğundan d 1 + d 2 = 24 olur. Cevap: 24.
Görev 6. Paralelkenarın kenarları 4 ve 6'dır. Köşegenler arasındaki dar açı 45 derecedir. Paralelkenarın alanını bulun. Çözüm.
1. AOB üçgeninden kosinüs teoremini kullanarak paralelkenarın kenarı ile köşegenler arasındaki ilişkiyi yazıyoruz. AB 2 = AO 2 + VO 2 2 · AO · VO · çünkü AOB. 4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1/2) · (d 2 /2)cos 45o; d 1 2 /4 + d 2 2 /4 – 2 · (d 1/2) · (d 2 /2)√2/2 = 16. d 1 2 + d 2 2 – d 1 · d 2 √2 = 64. 2. Benzer şekilde AOD üçgeni için de bağıntıyı yazıyoruz. Bunu dikkate alalım<АОD = 135 о и cos 135 о = -cos 45 о = -√2/2. d 1 2 + d 2 2 + d 1 · d 2 √2 = 144 denklemini elde ederiz. 3. Bir sistemimiz var Birinciyi ikinci denklemden çıkararak 2d 1 · d 2 √2 = 80 elde ederiz veya d 1 d 2 = 80/(2√2) = 20√2 4. S ABCD = 1/2 AC ВD sin AOB = 1/2 d 1 d 2 sin α = 1/2 20√2 √2/2 = 10. Not: Bu ve önceki problemde, alanı hesaplamak için köşegenlerin çarpımına ihtiyacımız olduğunu öngörerek sistemi tamamen çözmeye gerek yoktur. Cevap: 10. Görev 7. Paralelkenarın alanı 96, kenarları 8 ve 15'tir. Küçük köşegenin karesini bulun. Çözüm.
1. S ABCD = AB · AD · sin ВAD. Formülde bir değişiklik yapalım. 96 = 8 · 15 · sin ВAD elde ederiz. Dolayısıyla günah ВAD = 4/5. 2. Çünkü VAD'ı bulalım. günah 2 VAD + cos 2 VAD = 1. (4/5) 2 + cos 2 VAD = 1. cos 2 VAD = 9/25. Problemin koşullarına göre küçük köşegenin uzunluğunu buluyoruz. ВАD açısı dar ise ВD köşegeni daha küçük olacaktır. O zaman VAD = 3/5 olduğundan. 3. ABD üçgeninden kosinüs teoremini kullanarak BD köşegeninin karesini buluyoruz. ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · çünkü ВAD. ВD 2 = 8 2 + 15 2 – 2 8 15 3/5 = 145. Cevap: 145.
Hala sorularınız mı var? Bir geometri problemini nasıl çözeceğinizi bilmiyor musunuz? web sitesi, materyalin tamamını veya bir kısmını kopyalarken kaynağa bir bağlantı gereklidir. Paralelkenar, karşılıklı kenarları çiftler halinde paralel olan bir dörtgendir. Aşağıdaki şekil ABCD paralelkenarını göstermektedir. AB kenarı CD kenarına paralel, BC kenarı ise AD kenarına paraleldir. Tahmin edebileceğiniz gibi paralelkenar dışbükey bir dörtgendir. Paralelkenarın temel özelliklerini ele alalım. 1. Paralelkenarda karşılıklı açılar ve zıt kenarlar eşittir. Bu özelliği kanıtlayalım - aşağıdaki şekilde gösterilen paralelkenarı düşünün. Çapraz BD onu iki eşit üçgene böler: ABD ve CBD. Açılar sırasıyla BC ve AD ve AB ve CD paralel çizgilerinin BD kesen noktasında çapraz olarak uzandığından, BD kenarı ve ona bitişik iki açı boyunca eşittirler. Bu nedenle AB = CD ve 2. Paralelkenarın köşegenleri kesişme noktasına göre ikiye bölünür. O noktası ABCD paralelkenarının AC ve BD köşegenlerinin kesişme noktası olsun. O halde AOB üçgeni ve COD üçgeni, yan ve iki komşu açı boyunca birbirine eşittir. (AB = CD çünkü bunlar paralelkenarın zıt kenarlarıdır. Ve açı1 = açı2 ve açı3 = açı4, AB ve CD doğruları sırasıyla AC ve BD kesantlarıyla kesiştiğinde çapraz açılara benzer.) Bundan şu sonuç çıkar: AO = OC ve OB = OD, bunun kanıtlanması gerekiyordu. Tüm ana özellikler aşağıdaki üç şekilde gösterilmektedir. "Büyük bir bilimsel keşif, büyük bir soruna çözüm sağlar, ancak her sorunun çözümünde bir miktar keşif vardır." Paralelkenarın karşılıklı kenarları birbirine eşittir. Kanıt. Verilen paralelkenar ABCD olsun. Ve köşegenlerinin O noktasında kesişmesine izin verin. Paralelkenarda karşılıklı açılar eşittir. Kanıt. Paralelkenarın köşegenleri kesişir ve kesişme noktasında ikiye ayrılır. Kanıt. Verilen paralelkenar ABCD olsun. AC köşegenini çizelim. Üzerine ortadaki O'yu işaretleyelim.DO segmentinin devamında DO'ya eşit olan OB 1 segmentini bir kenara koyacağız. Normal okullar için ders kitaplarında (örneğin, Pogorelovo'da) şu şekilde kanıtlanmıştır: köşegenler bir paralelkenarı 4 üçgene böler. Bir çifti düşünelim ve eşit olduklarını öğrenelim: tabanları zıt taraflardır, ona bitişik karşılık gelen açılar, paralel çizgilerle dikey açılar gibi eşittir. Yani köşegenlerin parçaları çiftler halinde eşittir. Tüm. Hepsi bu? İşin komik tarafı bu kısmın kanıtlanmasının çok daha zor olmasıdır. Bu arada, bu daha genel bir sonuçtan kaynaklanmaktadır: herhangi bir dışbükey dörtgenin köşegenleri kesişecektir, ancak dışbükey olmayan herhangi bir dörtgenin kesişmesi mümkün olmayacaktır. Bir kenar ve iki bitişik açı boyunca üçgenlerin eşitliği (üçgenlerin eşitliğinin ikinci işareti) ve diğerleri. Thales, bir kenar boyunca iki üçgenin ve iki komşu açının eşitliği teoremine önemli bir pratik uygulama buldu. Denizdeki bir geminin mesafesini belirlemek için Milet limanına bir uzaklık ölçer inşa edildi. Üç adet tahrikli A, B ve C çivisinden (AB = BC) ve CA'ya dik işaretli bir düz çizgi SC'den oluşuyordu. SK düz çizgisi üzerinde bir gemi göründüğünde, D, .B ve E noktaları aynı düz çizgi üzerinde olacak şekilde D noktasını bulduk. Çizimden de anlaşılacağı üzere yerdeki CD mesafesi gemiye olan istenilen mesafedir. Ders üzerinde çalıştık Kuznetsov A.V. Poturnak S.A. Evgeniy Petrov Modern eğitim hakkında bir soru sorabilir, bir fikri ifade edebilir veya acil bir sorunu çözebilirsiniz. Eğitim forumu Yeni düşünce ve eylemden oluşan bir eğitim konseyinin uluslararası alanda toplandığı yer. Yarattıktan Blog, Yalnızca yetkin bir öğretmen olarak statünüzü geliştirmekle kalmayacak, aynı zamanda geleceğin okulunun gelişimine de önemli bir katkı sağlayacaksınız. Eğitim Liderleri Birliğiüst düzey uzmanlara kapıları açar ve onları dünyanın en iyi okullarını yaratma konusunda işbirliği yapmaya davet eder.
(
(Çünkü bir dik üçgende 30°'lik açının karşısındaki kenar hipotenüsün yarısına eşittir).
 alanıdır.
alanıdır.
(d1 + d2 = 140.
(d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Bir öğretmenden yardım almak için kaydolun.
İlk ders ücretsiz!
Paralelkenarın özellikleri

M.Ö. = MS. Ve 1, 2, 3 ve 4 açılarının eşitliğinden, A açısı = açı1 + açı3 = açı2 + açı4 = C açısı sonucu çıkar.
Ders konusu
Dersin Hedefleri
Dersin Hedefleri
Ders planı
giriiş

Paralelkenarın zıt kenarlarının özelliği
Üçgenlerin eşitliğinin ilk kriterine göre Δ AOB = Δ COD olduğundan (∠ AOB = ∠ COD, dikey olanlar olarak, AO=OC, DO=OB, paralelkenarın köşegenlerinin özelliğine göre), AB=CD. Aynı şekilde BOC ve DOA üçgenlerinin eşitliğinden BC = DA sonucu çıkar. Teorem kanıtlandı. Paralelkenarın zıt açılarının özelliği
Verilen paralelkenar ABCD olsun. Ve köşegenlerinin O noktasında kesişmesine izin verin.
Bir paralelkenarın karşıt kenarlarının özelliklerine ilişkin teoremde kanıtlanmış olandan Δ ABC = üç kenardaki Δ CDA (kanıtlanmış olandan AB=CD, BC=DA, AC – genel). Üçgenlerin eşitliğinden ∠ ABC = ∠ CDA sonucu çıkar.
Ayrıca ∠ ABD = ∠ CDB'den çıkan ∠ DAB = ∠ BCD olduğu da kanıtlanmıştır. Teorem kanıtlandı.Paralelkenarın köşegenlerinin özelliği
Önceki teoreme göre AB 1 CD bir paralelkenardır. Bu nedenle AB 1 doğrusu DC'ye paraleldir. Ancak A noktasından DC'ye paralel yalnızca bir doğru çizilebilir. Bu, düz AB 1'in düz AB ile çakıştığı anlamına gelir.
Ayrıca BC 1'in BC ile çakıştığı da kanıtlanmıştır. Bu, C noktasının C1 ile çakıştığı anlamına gelir. ABCD paralelkenarı AB 1 CD paralelkenarı ile çakışıyor. Sonuç olarak, paralelkenarın köşegenleri kesişir ve kesişme noktasında ikiye bölünür. Teorem kanıtlandı.
Yukarıda, kesişme noktasının, eğer varsa, köşegenleri ikiye böldüğü kanıtlanmıştır. Yukarıdaki mantık hiçbir şekilde onun varlığını kanıtlamaz. Yani, "paralelkenarın köşegenleri kesişir" teoreminin bir kısmı kanıtlanmamıştır.
Sorular
Kullanılan kaynakların listesi


