รากที่สองของความแปรปรวนเรียกว่าค่าเบี่ยงเบนมาตรฐานจากค่าเฉลี่ย ซึ่งคำนวณได้ดังนี้

ประถมศึกษา การแปลงพีชคณิตสูตรค่าเบี่ยงเบนมาตรฐานนำไปสู่รูปแบบต่อไปนี้:

สูตรนี้มักจะสะดวกกว่าในการฝึกคำนวณ

เฉลี่ย ส่วนเบี่ยงเบนมาตรฐานเช่นเดียวกับค่าเฉลี่ย ส่วนเบี่ยงเบนเชิงเส้นแสดงให้เห็นว่าค่าเฉพาะโดยเฉลี่ยของคุณลักษณะเบี่ยงเบนไปจากค่าเฉลี่ยเท่าใด ค่าเบี่ยงเบนมาตรฐานจะมากกว่าค่าเบี่ยงเบนเชิงเส้นเฉลี่ยเสมอ มีความสัมพันธ์ระหว่างพวกเขาดังต่อไปนี้:

เมื่อทราบอัตราส่วนนี้แล้ว คุณสามารถใช้ตัวบ่งชี้ที่ทราบเพื่อระบุค่าที่ไม่ทราบได้ เป็นต้น (ฉัน คำนวณ a และในทางกลับกัน ค่าเบี่ยงเบนมาตรฐานจะวัดขนาดสัมบูรณ์ของความแปรปรวนของคุณลักษณะและแสดงเป็นหน่วยการวัดเดียวกันกับค่าของคุณลักษณะ (รูเบิล ตัน ปี ฯลฯ) เป็นการวัดความแปรปรวนโดยสมบูรณ์

สำหรับ สัญญาณทางเลือก, เช่น การมีอยู่หรือไม่มี อุดมศึกษา, สูตรประกันภัย, การกระจายตัว และส่วนเบี่ยงเบนมาตรฐาน มีดังนี้

ให้เราแสดงการคำนวณค่าเบี่ยงเบนมาตรฐานตามข้อมูลของชุดข้อมูลที่ไม่ต่อเนื่องซึ่งแสดงลักษณะการกระจายตัวของนักศึกษาในคณะมหาวิทยาลัยแห่งใดแห่งหนึ่งตามอายุ (ตาราง 6.2)

ตารางที่ 6.2.

ผลลัพธ์ของการคำนวณเสริมแสดงไว้ในคอลัมน์ 2-5 ของตาราง 6.2.

อายุเฉลี่ยของนักเรียน ปี ถูกกำหนดโดยสูตรค่าเฉลี่ยเลขคณิตถ่วงน้ำหนัก (คอลัมน์ 2):

กำลังสองส่วนเบี่ยงเบน อายุของแต่ละบุคคลนักเรียนจากค่าเฉลี่ยจะอยู่ในคอลัมน์ 3-4 และผลิตภัณฑ์ของกำลังสองของการเบี่ยงเบนตามความถี่ที่สอดคล้องกันจะมีอยู่ในคอลัมน์ 5

เราหาความแปรปรวนของอายุ ปี ของนักเรียน โดยใช้สูตร (6.2) ดังนี้

จากนั้น o = l/3.43 1.85 *oda เช่น ค่าเฉพาะของอายุของนักเรียนแต่ละคนเบี่ยงเบนไปจากค่าเฉลี่ย 1.85 ปี

ค่าสัมประสิทธิ์ของการแปรผัน

ในค่าสัมบูรณ์ ค่าเบี่ยงเบนมาตรฐานไม่เพียงขึ้นอยู่กับระดับความแปรผันของคุณลักษณะเท่านั้น แต่ยังขึ้นอยู่กับระดับสัมบูรณ์ของตัวเลือกและค่าเฉลี่ยด้วย ดังนั้นจึงเป็นไปไม่ได้ที่จะเปรียบเทียบค่าเบี่ยงเบนมาตรฐานของอนุกรมความแปรผันกับระดับค่าเฉลี่ยที่แตกต่างกันได้โดยตรง เพื่อให้สามารถเปรียบเทียบได้คุณต้องค้นหา ความถ่วงจำเพาะค่าเบี่ยงเบนเฉลี่ย (เชิงเส้นหรือกำลังสอง) ในค่าเฉลี่ยเลขคณิตแสดงเป็นเปอร์เซ็นต์เช่น คำนวณ การวัดความสัมพันธ์ของการแปรผัน

ค่าสัมประสิทธิ์เชิงเส้นของการแปรผัน คำนวณโดยสูตร

ค่าสัมประสิทธิ์ของการแปรผัน กำหนดโดยสูตรต่อไปนี้:

ในค่าสัมประสิทธิ์ของการแปรผัน ไม่เพียงแต่จะกำจัดความเข้ากันไม่ได้ที่เกี่ยวข้องกับหน่วยการวัดที่แตกต่างกันของคุณลักษณะที่กำลังศึกษาเท่านั้น แต่ยังรวมถึงความเข้ากันไม่ได้ที่เกิดขึ้นเนื่องจากความแตกต่างในค่าของค่าเฉลี่ยเลขคณิตด้วย นอกจากนี้ ตัวบ่งชี้ความแปรผันยังระบุลักษณะความเป็นเนื้อเดียวกันของประชากร ประชากรจะถือว่าเป็นเนื้อเดียวกันหากค่าสัมประสิทธิ์การเปลี่ยนแปลงไม่เกิน 33%

ตามตารางครับ. 6.2 และผลการคำนวณที่ได้รับข้างต้น เรากำหนดค่าสัมประสิทธิ์การเปลี่ยนแปลง % ตามสูตร (6.3):

หากค่าสัมประสิทธิ์ความแปรผันเกิน 33% แสดงว่ามีความหลากหลายของประชากรที่กำลังศึกษา ค่าที่ได้รับในกรณีของเราบ่งชี้ว่าประชากรของนักเรียนตามอายุมีองค์ประกอบเป็นเนื้อเดียวกัน ดังนั้น, ฟังก์ชั่นที่สำคัญตัวบ่งชี้ทั่วไปของความแปรปรวน - การประเมินความน่าเชื่อถือของค่าเฉลี่ย ยิ่งน้อย. c1, ก2 และ วี ยิ่งชุดผลลัพธ์ของปรากฏการณ์เป็นเนื้อเดียวกันมากขึ้นเท่าใด และค่าเฉลี่ยผลลัพธ์ก็จะยิ่งเชื่อถือได้มากขึ้นเท่านั้น ตาม "กฎสามซิกมา" ที่พิจารณาโดยสถิติทางคณิตศาสตร์ ในรูปแบบการแจกแจงปกติหรืออนุกรมที่ใกล้เคียง ค่าเบี่ยงเบนจากค่าเฉลี่ยเลขคณิตไม่เกิน ±3 เกิดขึ้นใน 997 กรณีจาก 1,000 กรณี ดังนั้น เมื่อทราบ เอ็กซ์ และ a คุณจะได้รับแนวคิดเบื้องต้นทั่วไปเกี่ยวกับซีรีส์รูปแบบต่างๆ ตัวอย่างเช่น หากเงินเดือนเฉลี่ยของพนักงานในบริษัทคือ 25,000 รูเบิล และ a เท่ากับ 100 รูเบิล ดังนั้นด้วยความน่าจะเป็นที่เกือบจะแน่นอน เราสามารถพูดได้ว่าค่าจ้างของพนักงานของ บริษัท มีความผันผวนภายในช่วง (25,000 ± ± 3 x 100 ) เช่น จาก 24,700 ถึง 25,300 รูเบิล

กำหนดเป็นลักษณะทั่วไปของขนาดของการเปลี่ยนแปลงของลักษณะโดยรวม มันเท่ากับรากที่สองของค่าเบี่ยงเบนกำลังสองเฉลี่ยของแต่ละค่าของคุณลักษณะจากค่าเฉลี่ยเลขคณิตเช่น รากของ และ สามารถพบได้ดังนี้:

1. สำหรับแถวหลัก:

2. สำหรับซีรี่ส์รูปแบบ:

การแปลงสูตรค่าเบี่ยงเบนมาตรฐานจะทำให้มีรูปแบบที่สะดวกยิ่งขึ้นสำหรับการคำนวณเชิงปฏิบัติ:

เฉลี่ย ส่วนเบี่ยงเบนมาตรฐาน กำหนดว่าตัวเลือกเฉพาะโดยเฉลี่ยเบี่ยงเบนไปจากค่าเฉลี่ยมากน้อยเพียงใด และยังเป็นตัววัดความแปรปรวนของคุณลักษณะโดยสมบูรณ์และแสดงในหน่วยเดียวกับตัวเลือก ดังนั้นจึงมีการตีความอย่างดี

ตัวอย่างการหาค่าเบี่ยงเบนมาตรฐาน: ,

สำหรับคุณลักษณะทางเลือก สูตรค่าเบี่ยงเบนมาตรฐานจะมีลักษณะดังนี้:

โดยที่ p คือสัดส่วนของหน่วยในประชากรที่มีลักษณะเฉพาะ

q คือสัดส่วนของหน่วยที่ไม่มีลักษณะนี้

แนวคิดเรื่องค่าเบี่ยงเบนเชิงเส้นเฉลี่ย

ค่าเบี่ยงเบนเชิงเส้นเฉลี่ยถูกกำหนดให้เป็นค่าเฉลี่ยเลขคณิตของค่าสัมบูรณ์ของการเบี่ยงเบนของแต่ละตัวเลือกจาก

1. สำหรับแถวหลัก:

2. สำหรับซีรี่ส์รูปแบบ:

โดยที่ผลรวม n อยู่ ผลรวมของความถี่ของอนุกรมความแปรผัน.

ตัวอย่างการค้นหาค่าเบี่ยงเบนเชิงเส้นเฉลี่ย:

ข้อดีของค่าเบี่ยงเบนสัมบูรณ์เฉลี่ยเป็นการวัดการกระจายตัวในช่วงของการแปรผันนั้นชัดเจน เนื่องจากการวัดนี้ขึ้นอยู่กับการพิจารณาทั้งหมด การเบี่ยงเบนที่เป็นไปได้- แต่ตัวบ่งชี้นี้มีข้อบกพร่องที่สำคัญ การปฏิเสธสัญญาณพีชคณิตของการเบี่ยงเบนโดยพลการสามารถนำไปสู่ความจริงที่ว่าคุณสมบัติทางคณิตศาสตร์ของตัวบ่งชี้นี้อยู่ไกลจากระดับประถมศึกษา ซึ่งทำให้เป็นเรื่องยากมากที่จะใช้ค่าเบี่ยงเบนสัมบูรณ์เฉลี่ยเมื่อแก้ไขปัญหาที่เกี่ยวข้องกับการคำนวณความน่าจะเป็น

ดังนั้นค่าเบี่ยงเบนเชิงเส้นเฉลี่ยเป็นการวัดความแปรผันของคุณลักษณะจึงไม่ค่อยถูกนำมาใช้ในการปฏิบัติทางสถิติ กล่าวคือเมื่อสรุปตัวบ่งชี้โดยไม่คำนึงถึงสัญญาณของบัญชีก็สมเหตุสมผลทางเศรษฐกิจ ด้วยความช่วยเหลือ เช่น การวิเคราะห์การหมุนเวียนของการค้าต่างประเทศ องค์ประกอบของคนงาน จังหวะการผลิต ฯลฯ

จัตุรัสเฉลี่ย

ใช้กำลังสองเฉลี่ยเช่น การคำนวณขนาดเฉลี่ยของด้านข้างของส่วนตัดเป็นสี่เหลี่ยมจัตุรัส เส้นผ่านศูนย์กลางเฉลี่ยของลำตัว ท่อ ฯลฯ แบ่งออกเป็น 2 ประเภท

ค่าเฉลี่ยกำลังสองอย่างง่าย หากเมื่อแทนที่ค่าแต่ละค่าของคุณลักษณะด้วย ค่าเฉลี่ยหากจำเป็นต้องรักษาผลรวมของกำลังสองของค่าเดิมให้คงที่ ค่าเฉลี่ยจะเป็นค่าเฉลี่ยกำลังสอง

มันคือรากที่สองของผลหารของการหารผลรวมของกำลังสองของค่าคุณลักษณะแต่ละรายการด้วยหมายเลข:

ค่าเฉลี่ยกำลังสองถ่วงน้ำหนักคำนวณโดยใช้สูตร:

โดยที่ f คือเครื่องหมายน้ำหนัก

ลูกบาศก์เฉลี่ย

ใช้ลูกบาศก์เฉลี่ยตัวอย่างเช่น เมื่อกำหนดความยาวเฉลี่ยของด้านและลูกบาศก์ แบ่งออกเป็นสองประเภท
ลูกบาศก์เฉลี่ยอย่างง่าย:

เมื่อคำนวณค่าเฉลี่ยและความแปรปรวนในชุดการแจกแจงช่วงเวลา ค่าจริงของแอตทริบิวต์จะถูกแทนที่ ค่ากลางช่วงเวลาที่แตกต่างจากค่าเฉลี่ยเลขคณิตของค่าที่รวมอยู่ในช่วงเวลา สิ่งนี้นำไปสู่ข้อผิดพลาดอย่างเป็นระบบเมื่อคำนวณความแปรปรวน วี.เอฟ. เชพพาร์ดตัดสินใจอย่างนั้น ข้อผิดพลาดในการคำนวณผลต่างที่เกิดจากการใช้ข้อมูลที่จัดกลุ่มเป็น 1/12 ของกำลังสองของค่าช่วงเวลา ทั้งในทิศทางที่เพิ่มขึ้นและในทิศทางที่ขนาดของการกระจายตัวลดลง

การแก้ไขเชปปาร์ดควรใช้หากการแจกแจงใกล้เคียงกับปกติ เกี่ยวข้องกับคุณลักษณะที่มีลักษณะของการแปรผันอย่างต่อเนื่อง และขึ้นอยู่กับข้อมูลเริ่มต้นจำนวนมาก (n > 500) อย่างไรก็ตาม จากข้อเท็จจริงที่ว่าในบางกรณี ข้อผิดพลาดทั้งสองซึ่งกระทำไปในทิศทางต่างกันจะชดเชยซึ่งกันและกัน บางครั้งจึงเป็นไปได้ที่จะปฏิเสธที่จะแนะนำการแก้ไข

ยังไง มูลค่าน้อยลงความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน ยิ่งประชากรมีความเป็นเนื้อเดียวกันมากขึ้นและค่าเฉลี่ยโดยทั่วไปก็จะยิ่งมากขึ้น
ในทางปฏิบัติด้านสถิติ มักจำเป็นต้องเปรียบเทียบความแปรผัน สัญญาณต่างๆ- ตัวอย่างเช่น การเปรียบเทียบความแตกต่างด้านอายุของคนงานและคุณสมบัติ ระยะเวลาในการทำงาน และขนาดเป็นเรื่องที่น่าสนใจอย่างยิ่ง ค่าจ้างต้นทุนและกำไร ระยะเวลาในการให้บริการและผลิตภาพแรงงาน ฯลฯ สำหรับการเปรียบเทียบดังกล่าว ตัวบ่งชี้ความแปรปรวนสัมบูรณ์ของลักษณะไม่เหมาะสม: เป็นไปไม่ได้ที่จะเปรียบเทียบความแปรปรวนของประสบการณ์การทำงานซึ่งแสดงเป็นปีกับการเปลี่ยนแปลงของค่าจ้างซึ่งแสดงเป็นรูเบิล

ในการดำเนินการเปรียบเทียบดังกล่าว รวมถึงการเปรียบเทียบความแปรปรวนของคุณลักษณะเดียวกันในประชากรหลายกลุ่มที่มีค่าเฉลี่ยเลขคณิตต่างกัน จะใช้ตัวบ่งชี้สัมพัทธ์ของการแปรผัน - สัมประสิทธิ์ของการแปรผัน

ค่าเฉลี่ยโครงสร้าง

เพื่อระบุลักษณะแนวโน้มศูนย์กลางในการแจกแจงทางสถิติ มักใช้เหตุผลร่วมกับค่าเฉลี่ยเลขคณิต ซึ่งเป็นค่าหนึ่งของคุณลักษณะ X ซึ่งเนื่องจากคุณลักษณะบางอย่างของตำแหน่งในชุดการแจกแจง จึงสามารถกำหนดลักษณะระดับของมันได้

นี่เป็นสิ่งสำคัญอย่างยิ่งเมื่อในชุดการแจกแจงค่าสุดขีดของคุณลักษณะมีขอบเขตที่ไม่ชัดเจน ด้วยเหตุนี้ คำจำกัดความที่แม่นยำค่าเฉลี่ยเลขคณิตมักจะเป็นไปไม่ได้หรือยากมาก ในกรณีเช่นนี้ ระดับกลางสามารถกำหนดได้โดยการใช้ค่าคุณลักษณะที่อยู่ตรงกลางของอนุกรมความถี่หรือที่เกิดขึ้นบ่อยที่สุดในอนุกรมปัจจุบัน

ค่าดังกล่าวขึ้นอยู่กับลักษณะของความถี่เท่านั้น เช่น โครงสร้างของการกระจาย เป็นเรื่องปกติในตำแหน่งในชุดความถี่ดังนั้นค่าดังกล่าวจึงถือเป็นลักษณะของจุดศูนย์กลางของการแจกแจงดังนั้นจึงได้รับคำจำกัดความของค่าเฉลี่ยโครงสร้าง พวกเขาใช้ในการเรียน โครงสร้างภายในและโครงสร้างของชุดการแจกแจงของค่าคุณลักษณะ ตัวชี้วัดดังกล่าวได้แก่:

ค่าเบี่ยงเบนมาตรฐานเป็นหนึ่งในคำศัพท์ทางสถิติในโลกธุรกิจที่ให้ความน่าเชื่อถือแก่ผู้ที่จัดการเพื่อดึงมันออกมาได้ดีในการสนทนาหรือการนำเสนอ ขณะเดียวกันก็ทิ้งความเข้าใจผิดที่คลุมเครือในหมู่ผู้ที่ไม่รู้ว่ามันคืออะไรแต่รู้สึกเขินอายเกินกว่าจะเข้าใจได้ ถาม. ในความเป็นจริง ผู้จัดการส่วนใหญ่ไม่เข้าใจแนวคิดเรื่องค่าเบี่ยงเบนมาตรฐาน และหากคุณเป็นหนึ่งในนั้น ก็ถึงเวลาที่คุณต้องหยุดใช้ชีวิตแบบโกหก ในบทความวันนี้ ฉันจะบอกคุณว่าการวัดทางสถิติที่ประเมินค่าต่ำเกินไปนี้สามารถช่วยให้คุณเข้าใจข้อมูลที่คุณกำลังทำงานด้วยได้ดีขึ้นได้อย่างไร

ค่าเบี่ยงเบนมาตรฐานวัดจากอะไร?

ลองนึกภาพว่าคุณเป็นเจ้าของร้านค้าสองแห่ง และเพื่อหลีกเลี่ยงการขาดทุน การควบคุมยอดคงเหลือในสต๊อกให้ชัดเจนเป็นสิ่งสำคัญ ด้วยความพยายามที่จะค้นหาว่าผู้จัดการคนใดจัดการสินค้าคงคลังได้ดีกว่า คุณจึงตัดสินใจวิเคราะห์สินค้าคงคลังในช่วง 6 สัปดาห์ที่ผ่านมา ต้นทุนสต็อกโดยเฉลี่ยรายสัปดาห์สำหรับร้านค้าทั้งสองแห่งอยู่ที่ประมาณเท่ากันและมีจำนวนประมาณ 32 หน่วยทั่วไป เมื่อมองแวบแรก ปริมาณการไหลบ่าโดยเฉลี่ยแสดงให้เห็นว่าผู้จัดการทั้งสองมีการปฏิบัติงานที่คล้ายคลึงกัน

แต่ถ้าคุณพิจารณากิจกรรมของร้านที่สองให้ละเอียดยิ่งขึ้น คุณจะมั่นใจได้ว่าแม้ว่าค่าเฉลี่ยจะถูกต้อง แต่ความแปรปรวนของหุ้นก็สูงมาก (ตั้งแต่ 10 ถึง 58 USD) ดังนั้นเราจึงสรุปได้ว่าค่าเฉลี่ยไม่ได้ประเมินข้อมูลอย่างถูกต้องเสมอไป นี่คือที่มาของค่าเบี่ยงเบนมาตรฐาน

ค่าเบี่ยงเบนมาตรฐานจะแสดงวิธีการกระจายค่าสัมพันธ์กับค่าเฉลี่ยในของเรา กล่าวอีกนัยหนึ่ง คุณสามารถเข้าใจได้ว่าการแพร่กระจายของน้ำท่าในแต่ละสัปดาห์มีขนาดใหญ่เพียงใด

ในตัวอย่างของเรา เราใช้ ฟังก์ชันเอ็กเซล STANDARD DEVIATION เพื่อคำนวณค่าเบี่ยงเบนมาตรฐานพร้อมกับค่าเฉลี่ย

ในกรณีของผู้จัดการคนแรก ค่าเบี่ยงเบนมาตรฐานคือ 2 ซึ่งบอกเราว่าโดยเฉลี่ยแต่ละค่าในกลุ่มตัวอย่างเบี่ยงเบนไปจากค่าเฉลี่ย 2 เรื่องนี้ดีมั้ย? ลองดูคำถามจากมุมที่ต่างออกไป ค่าเบี่ยงเบนมาตรฐานเป็น 0 บอกเราว่าแต่ละค่าในกลุ่มตัวอย่างเท่ากับค่าเฉลี่ย (ในกรณีของเรา 32.2) ดังนั้นค่าเบี่ยงเบนมาตรฐานของ 2 จึงไม่แตกต่างจาก 0 มากนัก แสดงว่าค่าส่วนใหญ่ใกล้เคียงกับค่าเฉลี่ย ยิ่งค่าเบี่ยงเบนมาตรฐานเข้าใกล้ 0 มากเท่าใด ค่าเฉลี่ยก็ยิ่งน่าเชื่อถือมากขึ้นเท่านั้น นอกจากนี้ ค่าเบี่ยงเบนมาตรฐานใกล้กับ 0 บ่งชี้ถึงความแปรปรวนเล็กน้อยในข้อมูล นั่นคือค่าการไหลบ่าที่มีค่าเบี่ยงเบนมาตรฐานเป็น 2 บ่งบอกถึงความสอดคล้องที่น่าทึ่งของผู้จัดการคนแรก

ในกรณีร้านที่สอง ค่าเบี่ยงเบนมาตรฐานคือ 18.9 นั่นคือต้นทุนของน้ำไหลบ่าโดยเฉลี่ยเบี่ยงเบนไป 18.9 จากค่าเฉลี่ยในแต่ละสัปดาห์ แพร่กระจายบ้า! ยิ่งค่าเบี่ยงเบนมาตรฐานอยู่ห่างจาก 0 มากเท่าใด ค่าเฉลี่ยก็ยิ่งมีความแม่นยำน้อยลงเท่านั้น ในกรณีของเรา ตัวเลข 18.9 บ่งชี้ว่าค่าเฉลี่ย (32.8 USD ต่อสัปดาห์) ไม่สามารถเชื่อถือได้ นอกจากนี้ยังบอกเราว่าการไหลบ่ารายสัปดาห์มีความผันแปรสูง

นี่คือแนวคิดเรื่องค่าเบี่ยงเบนมาตรฐานโดยสรุป แม้ว่าจะไม่ได้ให้ข้อมูลเชิงลึกเกี่ยวกับการวัดทางสถิติที่สำคัญอื่นๆ (โหมด, ค่ามัธยฐาน...) แต่จริงๆ แล้ว ค่าเบี่ยงเบนมาตรฐานมีบทบาทสำคัญในการคำนวณทางสถิติส่วนใหญ่ การทำความเข้าใจหลักการของค่าเบี่ยงเบนมาตรฐานจะช่วยให้กระบวนการทางธุรกิจของคุณกระจ่างขึ้น

จะคำนวณค่าเบี่ยงเบนมาตรฐานได้อย่างไร?

ทีนี้เรารู้แล้วว่าเลขเบี่ยงเบนมาตรฐานบอกอะไร ลองคิดดูว่ามันคำนวณอย่างไร

ลองดูชุดข้อมูลตั้งแต่ 10 ถึง 70 โดยเพิ่มขั้นละ 10 ดังที่คุณเห็น เราได้คำนวณค่าเบี่ยงเบนมาตรฐานสำหรับข้อมูลเหล่านั้นแล้วโดยใช้ฟังก์ชัน STANDARDEV ในเซลล์ H2 (สีส้ม)

ด้านล่างนี้เป็นขั้นตอนที่ Excel ใช้เพื่อไปถึงเวอร์ชัน 21.6

โปรดทราบว่าการคำนวณทั้งหมดจะแสดงเป็นภาพเพื่อความเข้าใจที่ดีขึ้น ในความเป็นจริง ใน Excel การคำนวณจะเกิดขึ้นทันที โดยละขั้นตอนทั้งหมดไว้เบื้องหลัง

ขั้นแรก Excel จะค้นหาค่าเฉลี่ยตัวอย่าง ในกรณีของเรา ค่าเฉลี่ยกลายเป็น 40 ซึ่งในขั้นตอนถัดไปจะถูกลบออกจากค่าตัวอย่างแต่ละค่า ความแตกต่างแต่ละอย่างที่ได้รับจะถูกยกกำลังสองและสรุปผล เราได้ผลรวมเท่ากับ 2800 ซึ่งต้องหารด้วยจำนวนองค์ประกอบตัวอย่างลบ 1 เนื่องจากเรามี 7 องค์ประกอบ ปรากฎว่าเราต้องหาร 2800 ด้วย 6 จากผลลัพธ์ที่เราพบ รากที่สองตัวเลขนี้จะเป็นค่าเบี่ยงเบนมาตรฐาน

สำหรับผู้ที่ไม่ชัดเจนเกี่ยวกับหลักการคำนวณค่าเบี่ยงเบนมาตรฐานโดยใช้การแสดงภาพ ฉันจะให้การตีความทางคณิตศาสตร์เพื่อค้นหาค่านี้

ฟังก์ชั่นสำหรับคำนวณค่าเบี่ยงเบนมาตรฐานใน Excel

Excel มีสูตรค่าเบี่ยงเบนมาตรฐานหลายประเภท สิ่งที่คุณต้องทำคือพิมพ์ =STDEV แล้วคุณจะเห็นเอง

เป็นที่น่าสังเกตว่าฟังก์ชัน STDEV.V และ STDEV.G (ฟังก์ชันแรกและฟังก์ชันที่สองในรายการ) ซ้ำกับฟังก์ชัน STDEV และ STDEV (ฟังก์ชันที่ห้าและหกในรายการ) ตามลำดับ ซึ่งยังคงอยู่เพื่อให้เข้ากันได้กับฟังก์ชันก่อนหน้า เวอร์ชันของ Excel

โดยทั่วไปความแตกต่างในการลงท้ายของฟังก์ชัน .B และ .G บ่งบอกถึงหลักการคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างหรือ ประชากร- ฉันได้อธิบายความแตกต่างระหว่างอาร์เรย์ทั้งสองนี้ไปแล้วในอันก่อนหน้า

คุณสมบัติพิเศษของฟังก์ชัน STANDARDEV และ STANDARDEV (ฟังก์ชันที่สามและสี่ในรายการ) คือเมื่อคำนวณค่าเบี่ยงเบนมาตรฐานของอาร์เรย์ ค่าตรรกะและข้อความจะถูกนำมาพิจารณาด้วย ข้อความและค่าบูลีนจริงคือ 1 และค่าบูลีนเท็จคือ 0 ฉันจินตนาการไม่ออกว่าสถานการณ์ใดที่ฉันต้องการฟังก์ชันทั้งสองนี้ ดังนั้นฉันจึงคิดว่าสามารถละเลยได้

เอ็กซ์ ฉัน -ตัวแปรสุ่ม (ปัจจุบัน)

เอ็กซ์– ค่าเฉลี่ยของตัวแปรสุ่มสำหรับตัวอย่างคำนวณโดยใช้สูตร:

ดังนั้น, ความแปรปรวนคือกำลังสองเฉลี่ยของการเบี่ยงเบน - นั่นคือคำนวณค่าเฉลี่ยก่อนแล้วจึงนำมา ความแตกต่างระหว่างค่าดั้งเดิมและค่าเฉลี่ยแต่ละรายการจะถูกยกกำลังสอง จะถูกบวกแล้วหารด้วยจำนวนค่าในประชากร

ความแตกต่างระหว่างค่าแต่ละค่ากับค่าเฉลี่ยสะท้อนถึงการวัดค่าเบี่ยงเบน มันถูกยกกำลังสองเพื่อให้การเบี่ยงเบนทั้งหมดกลายเป็นตัวเลขบวกโดยเฉพาะ และเพื่อหลีกเลี่ยงการทำลายการเบี่ยงเบนเชิงบวกและเชิงลบร่วมกันเมื่อรวมเข้าด้วยกัน จากนั้น เมื่อพิจารณาค่าเบี่ยงเบนกำลังสอง เราก็เพียงคำนวณค่าเฉลี่ยเลขคณิต

สารละลาย คำวิเศษ“การกระจายตัว” ประกอบด้วยคำสามคำนี้เท่านั้น: ค่าเฉลี่ย – สี่เหลี่ยม – ส่วนเบี่ยงเบน

ส่วนเบี่ยงเบนมาตรฐาน (MSD)

เมื่อหารากที่สองของความแปรปรวน เราจะได้สิ่งที่เรียกว่า “ ส่วนเบี่ยงเบนมาตรฐาน"มีชื่ออยู่ "ส่วนเบี่ยงเบนมาตรฐาน" หรือ "ซิกมา" (มาจากชื่ออักษรกรีก σ - สูตรสำหรับค่าเบี่ยงเบนมาตรฐานคือ:

ดังนั้น, การกระจายตัวคือซิกม่ากำลังสอง หรือคือค่าเบี่ยงเบนมาตรฐานกำลังสอง

ส่วนเบี่ยงเบนมาตรฐานเห็นได้ชัดว่ายังเป็นการกำหนดลักษณะการวัดการกระจายตัวของข้อมูล แต่ตอนนี้ (ไม่เหมือนกับการกระจายตัว) สามารถเปรียบเทียบกับข้อมูลดั้งเดิมได้ เนื่องจากมีหน่วยการวัดเท่ากัน (ซึ่งชัดเจนจากสูตรการคำนวณ) ช่วงของการแปรผันคือความแตกต่างระหว่างค่าสุดขั้ว ค่าเบี่ยงเบนมาตรฐานซึ่งเป็นหน่วยวัดความไม่แน่นอนยังเกี่ยวข้องกับการคำนวณทางสถิติหลายอย่างด้วย ด้วยความช่วยเหลือจะกำหนดระดับความแม่นยำของการประมาณการและการคาดการณ์ต่างๆ หากความแปรผันมีขนาดใหญ่มาก ค่าเบี่ยงเบนมาตรฐานก็จะสูงเช่นกัน ดังนั้นการคาดการณ์จะไม่ถูกต้อง ซึ่งจะแสดงในช่วงความเชื่อมั่นที่กว้างมาก เป็นต้น

ดังนั้นในวิธีการประมวลผลข้อมูลทางสถิติในการประเมินอสังหาริมทรัพย์ จึงใช้กฎซิกมาสองหรือสามข้อ ขึ้นอยู่กับความแม่นยำที่ต้องการของงาน

เพื่อเปรียบเทียบกฎสองซิกมาและกฎสามซิกมา เราใช้สูตรของ Laplace:

ฉ - ฉ ,

โดยที่ Ф(x) คือฟังก์ชันลาปลาซ

ค่าต่ำสุด

β = ค่าสูงสุด

s = ค่าซิกมา (ส่วนเบี่ยงเบนมาตรฐาน)

ก = ค่าเฉลี่ย

ในกรณีนี้ สูตรของ Laplace จะใช้รูปแบบพิเศษเมื่อขอบเขตของค่า α และ β ตัวแปรสุ่ม X มีระยะห่างเท่ากันจากจุดศูนย์กลางของการแจกแจง a = M(X) ด้วยจำนวนที่แน่นอน d: a = a-d, b = a+d หรือ (1) สูตร (1) กำหนดความน่าจะเป็นของการเบี่ยงเบนที่กำหนด d ของตัวแปรสุ่ม X c กฎหมายปกติการกระจายจากเธอ ความคาดหวังทางคณิตศาสตร์ม(X) = ก.

หากในสูตร (1) เราใช้ d = 2s และ d = 3s ตามลำดับ เราจะได้: (2), (3)

กฎสองซิกมา

เกือบจะเชื่อถือได้ (ด้วยความน่าจะเป็นความเชื่อมั่นที่ 0.954) ว่าค่าทั้งหมดของตัวแปรสุ่ม X ที่มีกฎการแจกแจงแบบปกติเบี่ยงเบนไปจากค่าคาดหวังทางคณิตศาสตร์ M(X) = a ด้วยจำนวนไม่เกิน 2 วินาที (ค่าเบี่ยงเบนมาตรฐานสองค่า ). ความน่าจะเป็นของความเชื่อมั่น (Pd) คือความน่าจะเป็นของเหตุการณ์ที่เป็นที่ยอมรับตามอัตภาพว่าเชื่อถือได้ (ความน่าจะเป็นมีค่าใกล้เคียงกับ 1)

เราจะมาอธิบายกฎสองซิกมาในเชิงเรขาคณิตกัน ในรูป รูปที่ 6 แสดงเส้นโค้งเกาส์เซียนพร้อมจุดศูนย์กลางการกระจาย a พื้นที่ที่ล้อมรอบด้วยเส้นโค้งทั้งหมดและแกน Ox เท่ากับ 1 (100%) และพื้นที่ของสี่เหลี่ยมคางหมูโค้งระหว่าง abscissas a–2s และ a+2s ตามกฎทูซิกมามีค่าเท่ากัน ถึง 0.954 (95.4% ของพื้นที่ทั้งหมด) พื้นที่ของพื้นที่แรเงาคือ 1-0.954 = 0.046 (»5% ของพื้นที่ทั้งหมด) พื้นที่เหล่านี้เรียกว่าบริเวณวิกฤติของตัวแปรสุ่ม ค่าของตัวแปรสุ่มที่ตกลงไปในบริเวณวิกฤตนั้นไม่น่าเป็นไปได้ และในทางปฏิบัติเป็นที่ยอมรับตามอัตภาพว่าเป็นไปไม่ได้

ความน่าจะเป็นของค่าที่เป็นไปไม่ได้แบบมีเงื่อนไขเรียกว่าระดับนัยสำคัญของตัวแปรสุ่ม ระดับนัยสำคัญสัมพันธ์กับความน่าจะเป็นของความเชื่อมั่นตามสูตร:

โดยที่ q คือระดับนัยสำคัญที่แสดงเป็นเปอร์เซ็นต์

กฎสามซิกมา เมื่อแก้ไขปัญหาที่ต้องการความน่าเชื่อถือมากขึ้น เมื่อนำความน่าจะเป็นของความเชื่อมั่น (Pd) เท่ากับ 0.997 (หรือแม่นยำยิ่งขึ้นคือ 0.9973) แทนที่จะเป็นกฎสองซิกมา ตามสูตร (3) กฎจะถูกใช้

สามซิกมา ตามกฎสามซิกมา

กล่าวอีกนัยหนึ่ง ความน่าจะเป็นที่ค่าสัมบูรณ์ของส่วนเบี่ยงเบนจะเกินสามเท่าของส่วนเบี่ยงเบนมาตรฐานนั้นน้อยมาก คือ 0.0027 = 1-0.9973 ซึ่งหมายความว่าจะมีกรณีนี้เกิดขึ้นเพียง 0.27% เหตุการณ์ดังกล่าวซึ่งยึดหลักความเป็นไปไม่ได้ของเหตุการณ์ที่ไม่น่าเป็นไปได้ถือได้ว่าเป็นไปไม่ได้ในทางปฏิบัติ เหล่านั้น. การสุ่มตัวอย่างมีความแม่นยำสูง

นี่คือสาระสำคัญของกฎสามซิกมา:

หากมีการแจกแจงตัวแปรสุ่มตามปกติ ค่าสัมบูรณ์ของการเบี่ยงเบนจากความคาดหวังทางคณิตศาสตร์จะไม่เกินสามเท่าของค่าเบี่ยงเบนมาตรฐาน (MSD)

ในทางปฏิบัติ กฎสามซิกมาถูกนำมาใช้ดังนี้: หากไม่ทราบการแจกแจงของตัวแปรสุ่มที่กำลังศึกษา แต่ตรงตามเงื่อนไขที่ระบุในกฎข้างต้น ก็มีเหตุผลที่จะถือว่าตัวแปรที่กำลังศึกษานั้นมีการกระจายตามปกติ ; มิฉะนั้นจะไม่มีการแจกแจงตามปกติ

ระดับความสำคัญจะขึ้นอยู่กับระดับความเสี่ยงที่อนุญาตและงานที่ทำอยู่ สำหรับการประเมินมูลค่าอสังหาริมทรัพย์ มักใช้ตัวอย่างที่แม่นยำน้อยกว่าตามกฎสองซิกมา

$X$. เริ่มต้นด้วยให้เราจำคำจำกัดความต่อไปนี้:

คำจำกัดความ 1

ประชากร- ชุดของวัตถุที่เลือกแบบสุ่มประเภทที่กำหนดซึ่งดำเนินการสังเกตเพื่อให้ได้ค่าเฉพาะของตัวแปรสุ่มซึ่งดำเนินการภายใต้สภาวะคงที่เมื่อศึกษาตัวแปรสุ่มประเภทที่กำหนด

คำจำกัดความ 2

ความแปรปรวนทั่วไป-- เฉลี่ย เลขคณิตของกำลังสองการเบี่ยงเบนของค่าของตัวแปรประชากรจากค่าเฉลี่ย

ปล่อยให้ค่าของตัวเลือก $x_1,\ x_2,\dots ,x_k$ มีความถี่ $n_1,\ n_2,\dots ,n_k$ ตามลำดับ จากนั้นความแปรปรวนทั่วไปจะคำนวณโดยใช้สูตร:

ลองพิจารณาดู กรณีพิเศษ- ให้ตัวเลือกทั้งหมด $x_1,\ x_2,\dots ,x_k$ แตกต่างกัน ในกรณีนี้ $n_1,\ n_2,\dots ,n_k=1$ เราพบว่าในกรณีนี้ ความแปรปรวนทั่วไปคำนวณโดยใช้สูตร:

แนวคิดนี้ยังเกี่ยวข้องกับแนวคิดเรื่องค่าเบี่ยงเบนมาตรฐานทั่วไปด้วย

คำจำกัดความ 3

ส่วนเบี่ยงเบนมาตรฐานทั่วไป

\[(\sigma )_g=\sqrt(D_g)\]

ความแปรปรวนตัวอย่าง

ขอให้เราได้รับประชากรตัวอย่างเทียบกับตัวแปรสุ่ม $X$ เริ่มต้นด้วยให้เราจำคำจำกัดความต่อไปนี้:

คำจำกัดความที่ 4

ประชากรตัวอย่าง-- ส่วนหนึ่งของวัตถุที่เลือกจากประชากรทั่วไป

คำจำกัดความที่ 5

ความแปรปรวนตัวอย่าง-- ค่าเฉลี่ยเลขคณิตของค่าของประชากรตัวอย่าง

ปล่อยให้ค่าของตัวเลือก $x_1,\ x_2,\dots ,x_k$ มีความถี่ $n_1,\ n_2,\dots ,n_k$ ตามลำดับ จากนั้นคำนวณความแปรปรวนตัวอย่างโดยใช้สูตร:

ลองพิจารณาเป็นกรณีพิเศษ ให้ตัวเลือกทั้งหมด $x_1,\ x_2,\dots ,x_k$ แตกต่างกัน ในกรณีนี้ $n_1,\ n_2,\dots ,n_k=1$ เราพบว่าในกรณีนี้ ความแปรปรวนตัวอย่างคำนวณโดยใช้สูตร:

ที่เกี่ยวข้องกับแนวคิดนี้คือแนวคิดเรื่องค่าเบี่ยงเบนมาตรฐานตัวอย่าง

คำนิยาม 6

ตัวอย่างค่าเบี่ยงเบนมาตรฐาน-- รากที่สองของความแปรปรวนทั่วไป:

\[(\sigma )_в=\sqrt(D_в)\]

แก้ไขความแปรปรวนแล้ว

ในการค้นหาความแปรปรวนที่แก้ไขแล้ว $S^2$ จำเป็นต้องคูณความแปรปรวนตัวอย่างด้วยเศษส่วน $\frac(n)(n-1)$ นั่นคือ

แนวคิดนี้ยังเกี่ยวข้องกับแนวคิดเรื่องค่าเบี่ยงเบนมาตรฐานที่แก้ไขแล้ว ซึ่งพบได้จากสูตร:

ในกรณีที่ค่าของตัวแปรไม่ต่อเนื่องกัน แต่เป็นตัวแทนของช่วงเวลา ดังนั้นในสูตรสำหรับการคำนวณความแปรปรวนทั่วไปหรือตัวอย่าง ค่าของ $x_i$ จะถูกนำมาเป็นค่าของจุดกึ่งกลางของช่วงเวลาถึง ซึ่ง $x_i.$ อยู่

ตัวอย่างโจทย์การหาความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน

ตัวอย่างที่ 1

ประชากรตัวอย่างถูกกำหนดโดยตารางการแจกจ่ายต่อไปนี้:

รูปที่ 1.

ลองหาค่าความแปรปรวนตัวอย่าง ค่าเบี่ยงเบนมาตรฐานตัวอย่าง ความแปรปรวนที่แก้ไข และค่าเบี่ยงเบนมาตรฐานที่แก้ไขแล้ว

เพื่อแก้ไขปัญหานี้ ขั้นแรกเราจะสร้างตารางการคำนวณ:

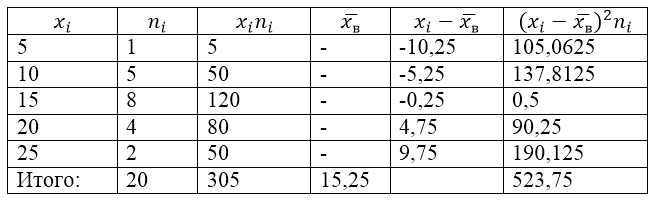
รูปที่ 2.

ค่า $\overline(x_в)$ (ค่าเฉลี่ยตัวอย่าง) ในตารางพบได้จากสูตร:

\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]

\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15.25\]

ลองหาความแปรปรวนตัวอย่างโดยใช้สูตร:

ตัวอย่างค่าเบี่ยงเบนมาตรฐาน:

\[(\sigma )_в=\sqrt(D_в)\ประมาณ 5.12\]

ความแปรปรวนที่แก้ไขแล้ว:

\[(S^2=\frac(n)(n-1)D)_в=\frac(20)(19)\cdot 26.1875\ประมาณ 27.57\]

แก้ไขค่าเบี่ยงเบนมาตรฐานแล้ว