Predstavili smo ga mi linearne operacije na vektorjih omogočajo ustvarjanje različnih izrazov za vektorske količine in jih preoblikovati z uporabo lastnosti, nastavljenih za te operacije.
Na podlagi danega niza vektorjev a 1, ..., a n lahko ustvarite izraz oblike
kjer so a 1, ... in n poljubna realna števila. Ta izraz se imenuje linearna kombinacija vektorjev a 1, ..., a n. Števila α i, i = 1, n, predstavljajo koeficienti linearne kombinacije. Imenuje se tudi niz vektorjev sistem vektorjev.
V povezavi z uvedenim konceptom linearne kombinacije vektorjev se pojavi problem opisovanja množice vektorjev, ki jo lahko zapišemo kot linearno kombinacijo danega sistema vektorjev a 1, ..., a n. Poleg tega obstajajo naravna vprašanja o pogojih, pod katerimi obstaja predstavitev vektorja v obliki linearne kombinacije, in o edinstvenosti takšne predstavitve.
Opredelitev 2.1. Imenujemo vektorje a 1, ... in n linearno odvisen, če obstaja nabor koeficientov α 1 , ... , α n tako, da
α 1 a 1 + ... + α n а n = 0 (2.2)
in vsaj eden od teh koeficientov je različen od nič. Če navedeni niz koeficientov ne obstaja, se vektorji pokličejo linearno neodvisen.
Če je α 1 = ... = α n = 0, potem je očitno α 1 a 1 + ... + α n a n = 0. S tem v mislih lahko rečemo to: vektorji a 1, ... in n so linearno neodvisni, če iz enačbe (2.2) sledi, da so vsi koeficienti α 1 , ... , α n enaki nič.
Naslednji izrek pojasnjuje, zakaj se novi koncept imenuje izraz "odvisnost" (ali "neodvisnost"), in zagotavlja preprosto merilo za linearno odvisnost.
Izrek 2.1. Da bi bili vektorji a 1, ... in n, n > 1, linearno odvisni, je nujno in zadostno, da je eden od njih linearna kombinacija drugih.
◄ Nujnost. Predpostavimo, da so vektorji a 1, ... in n linearno odvisni. Po definiciji 2.1 linearne odvisnosti je v enačbi (2.2) na levi strani vsaj en koeficient, ki ni nič, na primer α 1. Če pustimo prvi člen na levi strani enakosti, preostale premaknemo na desno stran in jim spremenimo predznake, kot običajno. Če dobljeno enakost delimo z α 1, dobimo
a 1 =-α 2 /α 1 ⋅ a 2 - ... - α n /α 1 ⋅ a n
tiste. predstavitev vektorja a 1 kot linearne kombinacije preostalih vektorjev a 2, ..., a n.
Ustreznost. Naj na primer prvi vektor a 1 predstavimo kot linearno kombinacijo preostalih vektorjev: a 1 = β 2 a 2 + ... + β n a n. Če vse člene prenesemo z desne strani na levo, dobimo a 1 - β 2 a 2 - ... - β n a n = 0, tj. linearna kombinacija vektorjev a 1, ..., a n s koeficienti α 1 = 1, α 2 = - β 2, ..., α n = - β n, enaka ničelni vektor. V tej linearni kombinaciji niso vsi koeficienti enaki nič. V skladu z definicijo 2.1 so vektorji a 1, ... in n linearno odvisni.
Definicija in merilo za linearno odvisnost sta oblikovana tako, da nakazujeta prisotnost dveh ali več vektorjev. Lahko pa govorimo tudi o linearni odvisnosti enega vektorja. Če želite uresničiti to možnost, morate namesto "vektorji linearno odvisni" reči "sistem vektorjev je linearno odvisen." Preprosto je videti, da izraz "sistem enega vektorja je linearno odvisen" pomeni, da je ta posamezen vektor enak nič (v linearni kombinaciji je samo en koeficient in ne sme biti enak nič).
Koncept linearne odvisnosti ima preprosto geometrijsko razlago. Naslednje tri izjave pojasnjujejo to razlago.
Izrek 2.2. Dva vektorja sta linearno odvisna, če in samo če sta kolinearni.
◄ Če sta vektorja a in b linearno odvisna, potem je eden od njiju, na primer a, izražen skozi drugega, tj. a = λb za neko realno število λ. Po definiciji 1.7 dela vektorjev na število, sta vektorja a in b kolinearna.
Naj bosta vektorja a in b kolinearna. Če sta oba nič, potem je očitno, da sta linearno odvisna, saj je vsaka njuna linearna kombinacija enaka ničelnemu vektorju. Naj eden od teh vektorjev ni enak 0, na primer vektor b. Označimo z λ razmerje dolžin vektorjev: λ = |a|/|b|. Kolinearni vektorji so lahko enosmerno oz nasprotno usmerjeni. V slednjem primeru spremenimo predznak λ. Nato se s preverjanjem definicije 1.7 prepričamo, da je a = λb. Po izreku 2.1 sta vektorja a in b linearno odvisna.
Opomba 2.1. V primeru dveh vektorjev, ob upoštevanju kriterija linearne odvisnosti, lahko dokazani izrek preoblikujemo na naslednji način: dva vektorja sta kolinearna, če in samo če je eden od njiju predstavljen kot produkt drugega s številom. To je priročen kriterij za kolinearnost dveh vektorjev.
Izrek 2.3. Trije vektorji so linearno odvisni, če in samo če komplanaren.
◄ Če so trije vektorji a, b, c linearno odvisni, potem je po izreku 2.1 eden od njih, na primer a, linearna kombinacija ostalih: a = βb + γc. Združimo izhodišča vektorjev b in c v točki A. Potem bosta imela vektorja βb, γс skupno izhodišče v točki A in vzdolž po pravilu paralelograma je njihova vsota tiste. vektor a bo vektor z izhodiščem A in konec, ki je oglišče paralelograma, sestavljenega iz komponentnih vektorjev. Tako vsi vektorji ležijo v isti ravnini, to je komplanarni.
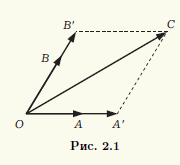
Naj bodo vektorji a, b, c komplanarni. Če je eden od teh vektorjev enak nič, potem bo to očitno linearna kombinacija ostalih. Dovolj je, da so vsi koeficienti linearne kombinacije enaki nič. Zato lahko predpostavimo, da vsi trije vektorji niso nič. Združljiv začela teh vektorjev v skupni točki O. Naj bodo njihovi konci točke A, B, C (slika 2.1). Skozi točko C narišemo premice, vzporedne premicam, ki potekajo skozi pare točk O, A in O, B. Če presečišča označimo kot A" in B", dobimo paralelogram OA"CB", torej OC" = OA" + OB". Vektor OA" in neničelni vektor a = OA sta kolinearna, zato lahko prvega od njiju dobimo tako, da drugega pomnožimo z realnim številom α:OA" = αOA. Podobno je OB" = βOB, β ∈ R. Posledično dobimo, da je OC" = α OA + βOB, tj. vektor c je linearna kombinacija vektorjev a in b. Po izreku 2.1 so vektorji a, b, c linearno odvisni.
Izrek 2.4. Kateri koli štirje vektorji so linearno odvisni.
◄ Dokaz izvedemo po isti shemi kot v izreku 2.3. Razmislite o poljubnih štirih vektorjih a, b, c in d. Če je eden od štirih vektorjev enak nič ali sta med njimi dva kolinearna vektorja ali so trije od štirih vektorjev koplanarni, potem so ti štirje vektorji linearno odvisni. Na primer, če sta vektorja a in b kolinearna, potem lahko naredimo njuno linearno kombinacijo αa + βb = 0 z neničelnimi koeficienti, nato pa tej kombinaciji dodamo preostala dva vektorja, pri čemer za koeficiente vzamemo ničle. Dobimo linearno kombinacijo štirih vektorjev enakih 0, v katerih so koeficienti različni od nič.
Tako lahko predpostavimo, da med izbranimi štirimi vektorji ni noben vektor nič, nobena dva nista kolinearna in noben trije niso komplanarni. Za njun skupni začetek izberimo točko O. Potem bodo konci vektorjev a, b, c, d nekatere točke A, B, C, D (slika 2.2). Skozi točko D narišemo tri ravnine, vzporedno z ravninami OBC, OCA, OAB in naj bodo A", B", C" točke presečišča teh ravnin s premicami OA, OB, OS. Dobimo paralelopiped OA"C"B"C"B"DA ", vektorji a, b, c pa ležijo na njegovih robovih, ki izhajajo iz oglišča O. Ker je štirikotnik OC"DC" paralelogram, potem je OD = OC" + OC". Po drugi strani pa je odsek OC" diagonala paralelogram OA"C"B", tako da je OC" = OA" + OB" in OD = OA" + OB" + OC" .
Upoštevati je treba, da so pari vektorjev OA ≠ 0 in OA" , OB ≠ 0 in OB" , OC ≠ 0 in OC" kolinearni, zato je možno izbrati koeficiente α, β, γ tako, da OA" = αOA, OB" = βOB in OC" = γOC. Končno dobimo OD = αOA + βOB + γOC. Posledično je vektor OD izražen preko ostalih treh vektorjev, vsi štirje vektorji pa so po izreku 2.1 linearno odvisni.
Opredelitev. Linearna kombinacija vektorjev a 1 , ..., a n s koeficienti x 1 , ..., x n imenujemo vektor
x 1 a 1 + ... + x n a n .
trivialno, če so vsi koeficienti x 1 , ..., x n enaki nič.
Opredelitev. Linearna kombinacija x 1 a 1 + ... + x n a n se imenuje netrivialno, če vsaj eden od koeficientov x 1, ..., x n ni enak nič.
linearno neodvisen, če ni nobene netrivialne kombinacije teh vektorjev, ki je enaka ničelnemu vektorju.
To pomeni, da so vektorji a 1, ..., a n linearno neodvisni, če je x 1 a 1 + ... + x n a n = 0, če in samo če je x 1 = 0, ..., x n = 0.
Opredelitev. Vektorji a 1, ..., a n se imenujejo linearno odvisen, če obstaja netrivialna kombinacija teh vektorjev, ki je enaka ničelnemu vektorju.
Lastnosti linearno odvisnih vektorjev:
Za n-dimenzionalne vektorje.
n + 1 vektorji so vedno linearno odvisni.
Za 2 in 3 dimenzionalne vektorje.
Dva linearno odvisna vektorja sta kolinearna. (Kolinearni vektorji so linearno odvisni.)
Za 3-dimenzionalne vektorje.
Trije linearno odvisni vektorji so komplanarni. (Trije koplanarni vektorji so linearno odvisni.)
Primeri problemov o linearni odvisnosti in linearni neodvisnosti vektorjev:
Primer 1. Preverite, ali so vektorji a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) linearno neodvisni. .
rešitev:
Vektorji bodo linearno odvisni, saj je dimenzija vektorjev manjša od števila vektorjev.
Primer 2. Preverite, ali so vektorji a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) linearno neodvisni.
rešitev:
| x 1 + x 2 = 0 | |
| x 1 + 2x 2 - x 3 = 0 | |
| x 1 + x 3 = 0 |
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 1 | 0 |
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 1 - 0 | 0 - 0 | 0 | -1 | 1 | 0 |
odštejte drugo od prve vrstice; tretji vrstici dodajte drugo vrstico:
| ~ | 1 - 0 | 1 - 1 | 0 - (-1) | 0 - 0 | ~ | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 + 0 | 0 | 0 | 0 | 0 |
Ta rešitev kaže, da ima sistem veliko rešitev, to je, da obstaja neničelna kombinacija vrednosti števil x 1, x 2, x 3, tako da je linearna kombinacija vektorjev a, b, c enaka ničelni vektor, na primer:
A + b + c = 0
kar pomeni, da so vektorji a, b, c linearno odvisni.
odgovor: vektorji a, b, c so linearno odvisni.
Primer 3. Preverite, ali so vektorji a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) linearno neodvisni.
rešitev: Poiščimo vrednosti koeficientov, pri katerih bo linearna kombinacija teh vektorjev enaka ničelnemu vektorju.
x 1 a + x 2 b + x 3 c 1 = 0To vektorsko enačbo lahko zapišemo kot sistem linearne enačbe
| x 1 + x 2 = 0 | |
| x 1 + 2x 2 - x 3 = 0 | |
| x 1 + 2x 3 = 0 |
Rešimo ta sistem z Gaussovo metodo
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 2 | 0 |
odštejte prvo od druge vrstice; odštejte prvo od tretje vrstice:
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 2 - 0 | 0 - 0 | 0 | -1 | 2 | 0 |
odštejte drugo od prve vrstice; tretji vrstici dodajte drugo.
Pustiti L je poljuben linearni prostor, a jaz Î L,- njegovi elementi (vektorji).
Opredelitev 3.3.1. Izraz , Kje , - poljubna realna števila, imenovana linearna kombinacija vektorji a 1, a 2,…, a n.
Če vektor R = , potem pravijo, da R razčleniti na vektorje a 1, a 2,…, a n.
Opredelitev 3.3.2. Linearna kombinacija vektorjev se imenuje netrivialno, če je med števili vsaj eno različno od nič. V nasprotnem primeru se imenuje linearna kombinacija trivialno.
Definicija 3.3.3 . Vektorji a 1 , a 2 ,…, a n se imenujejo linearno odvisni, če obstaja njihova netrivialna linearna kombinacija, taka da
= 0 .
Definicija 3.3.4. Vektorji a 1 ,a 2 ,…, a n imenujemo linearno neodvisne, če je enakost = 0 je mogoča le v primeru, ko so vsa števila l 1, l 2,…, l n so hkrati enake nič.
Upoštevajte, da lahko vsak neničelni element a 1 obravnavamo kot linearno neodvisen sistem, saj je enakost l a 1 = 0 mogoče le, če l= 0.
Izrek 3.3.1. Nujen in zadosten pogoj za linearno odvisnost a 1 , a 2 ,…, a n je možnost razgradnje vsaj enega od teh elementov na ostale.
Dokaz. Nujnost. Naj bodo elementi a 1 , a 2 ,…, a n linearno odvisen. To pomeni, da = 0 , in vsaj eno od številk l 1, l 2,…, l n drugačen od nič. Naj za gotovost l 1 ¹ 0. Potem
tj. element a 1 se razgradi na elemente a 2 , a 3 , …, a n.
Ustreznost. Naj bo element a 1 razstavljen na elemente a 2 , a 3 , …, a n, tj. a 1 = . Potem 
= 0
, torej obstaja netrivialna linearna kombinacija vektorjev a 1 , a 2 ,…, a n, enako 0
, torej so linearno odvisni .
Izrek 3.3.2. Če je vsaj eden od elementov a 1 , a 2 ,…, a n nič, potem so ti vektorji linearno odvisni.
Dokaz . Pustiti a n= 0 , nato = 0 , kar pomeni linearno odvisnost teh elementov.
Izrek 3.3.3. Če je med n vektorji katerikoli p (p< n) векторов линейно зависимы, то и все n элементов линейно зависимы.
Dokaz. Naj bodo za določnost elementi a 1 , a 2 ,…, a str linearno odvisen. To pomeni, da obstaja netrivialna linearna kombinacija, tako da = 0 . Navedena enakost bo ohranjena, če element dodamo obema njegovima deloma. Potem + = 0 , in vsaj eno od številk l 1, l 2,…, lp drugačen od nič. Zato so vektorji a 1 , a 2 ,…, a n so linearno odvisni.
Posledica 3.3.1.Če je n elementov linearno neodvisnih, potem je vsak k izmed njih linearno neodvisen (k< n).
Izrek 3.3.4. Če vektorji a 1, a 2,…, a n- 1 so linearno neodvisni in elementi a 1, a 2,…, a n- 1, a n so linearno odvisni, potem vektor a n lahko razširimo v vektorje a 1, a 2,…, a n- 1 .
Dokaz. Ker je po pogoju a 1 , a 2 ,…,a n- 1, a n so linearno odvisni, potem obstaja njihova netrivialna linearna kombinacija = 0 , in (sicer se bodo izkazali za linearne odvisni vektorji a 1, a 2,…, a n- 1). Ampak potem vektor
,
Q.E.D.
Vektorski sistem se imenuje linearno odvisen, če obstajajo števila, med katerimi je vsaj eno različno od nič, tako da velja enakost https://pandia.ru/text/78/624/images/image004_77.gif" width="57" height="24 src= " >.
Če je ta enakost izpolnjena samo v primeru, ko je vse , se imenuje sistem vektorjev linearno neodvisen.
Izrek. Vektorski sistem bo linearno odvisenče in samo če je vsaj eden od njegovih vektorjev linearna kombinacija ostalih.
Primer 1. Polinom 
je linearna kombinacija polinomov https://pandia.ru/text/78/624/images/image010_46.gif" width="88 height=24" height="24">. Polinomi sestavljajo linearno neodvisen sistem, saj polinom https: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.
Primer 2. Matrični sistem, , https://pandia.ru/text/78/624/images/image016_37.gif" width="51" height="48 src="> je linearno neodvisen, saj je linearna kombinacija enaka ničelna matrika samo v primeru, ko https://pandia.ru/text/78/624/images/image019_27.gif" width="69" height="21">, , https://pandia.ru/text /78/624 /images/image022_26.gif" width="40" height="21"> linearno odvisno.
rešitev.
Naredimo linearno kombinacijo teh vektorjev https://pandia.ru/text/78/624/images/image023_29.gif" width="97" height="24">=0..gif" width="360" višina=" 22">.
Če izenačimo enake koordinate enakih vektorjev, dobimo https://pandia.ru/text/78/624/images/image027_24.gif" width="289" height="69">
Končno dobimo
in
Sistem ima edinstveno trivialno rešitev, zato je linearna kombinacija teh vektorjev enaka nič le v primeru, ko so vsi koeficienti enaki nič. Zato je ta sistem vektorjev linearno neodvisen.
Primer 4. Vektorja sta linearno neodvisna. Kakšni bodo vektorski sistemi?
a).
;
b).
?
rešitev.
a). Naredimo linearno kombinacijo in jo enačimo z nič
Z uporabo lastnosti operacij z vektorji v linearnem prostoru prepišemo zadnjo enakost v obliki
Ker sta vektorja linearno neodvisna, morajo biti koeficienti pri enaki nič, tj..gif" width="12" height="23 src=">
Nastali sistem enačb ima edinstveno trivialno rešitev 
.
Od enakosti (*) izvaja se le, če https://pandia.ru/text/78/624/images/image031_26.gif" width="115 height=20" height="20"> – linearno neodvisno;
b). Naredimo enakost https://pandia.ru/text/78/624/images/image039_17.gif" width="265" height="24 src="> (**)
Z uporabo podobnega sklepanja dobimo
Z reševanjem sistema enačb po Gaussovi metodi dobimo
oz
Slednji sistem ima neskončno število rešitev https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. Tako obstaja ne- ničelna množica koeficientov, za katere velja enakost (**)
. Zato sistem vektorjev – linearno odvisen.
Primer 5 Sistem vektorjev je linearno neodvisen in sistem vektorjev je linearno odvisen..gif" width="80" height="24">.gif" width="149 height=24" height="24"> (***)
V enakopravnosti (***) . Dejansko bi bil pri , sistem linearno odvisen.
Iz relacije (***)
dobimo 
oz 
Označimo 
.
Dobimo 
Naloge za neodvisna odločitev(v občinstvu)
1. Sistem, ki vsebuje ničelni vektor, je linearno odvisen.
2. Sistem, sestavljen iz enega vektorja A, je linearno odvisna, če in samo če, a=0.
3. Sistem, sestavljen iz dveh vektorjev, je linearno odvisen, če in samo če sta vektorja sorazmerna (to pomeni, da enega od njiju dobimo iz drugega z množenjem s številom).
4. Če linearno odvisnemu sistemu dodate vektor, dobite linearno odvisen sistem.
5. Če vektor odstranimo iz linearno neodvisnega sistema, potem je nastali sistem vektorjev linearno neodvisen.
6. Če sistem S je linearno neodvisen, vendar postane linearno odvisen, ko dodamo vektor b, nato vektor b linearno izražena s sistemskimi vektorji S.
c). Sistem matrik , , v prostoru matrik drugega reda.
10. Naj sistem vektorjev a,b,c vektorski prostor je linearno neodvisen. Dokažite linearno neodvisnost naslednjih vektorskih sistemov:
a).a+b, b, c.
b).a+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">– poljubno število
c).a+b, a+c, b+c.
11. Pustiti a,b,c– trije vektorji na ravnini, iz katerih je mogoče sestaviti trikotnik. Ali bodo ti vektorji linearno odvisni?
12. Podana sta dva vektorja a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). Poiščite še dva štiridimenzionalna vektorja a3 ina4 tako da sistem a1,a2,a3,a4 je bil linearno neodvisen .
Naloga 1. Ugotovite, ali je sistem vektorjev linearno neodvisen. Sistem vektorjev bo določen z matriko sistema, katere stolpce sestavljajo koordinate vektorjev.
.
rešitev. Naj linearna kombinacija 
enako nič. Ko to enakost zapišemo v koordinate, dobimo naslednji sistem enačb:
.
Takšen sistem enačb imenujemo trikotni. Ima samo eno rešitev 
. Zato vektorji 
linearno neodvisen.
Naloga 2. Ugotovite, ali je sistem vektorjev linearno neodvisen.
.
rešitev. Vektorji 
so linearno neodvisni (glej problem 1). Dokažimo, da je vektor linearna kombinacija vektorjev 
. Vektorski raztezni koeficienti 
se določijo iz sistema enačb
.
Ta sistem, tako kot trikotni, ima edinstveno rešitev.
Zato sistem vektorjev 
linearno odvisen.
Komentiraj. Imenujemo matrike istega tipa kot v nalogi 1 trikotne in v nalogi 2 – stopničasto trikoten . Vprašanje linearne odvisnosti sistema vektorjev je enostavno rešiti, če je matrika, sestavljena iz koordinat teh vektorjev, stopničasta trikotna. Če matrika nima posebna vrsta, nato z uporabo osnovne pretvorbe nizov , ki ohranja linearne odnose med stolpci, ga je mogoče zmanjšati na stopničasto trikotno obliko.
Osnovne pretvorbe nizov imenujemo matrike (EPS). naslednje operacije nad matriko:
1) preureditev linij;
2) množenje niza z neničelnim številom;
3) dodajanje drugega niza nizu, pomnoženega s poljubnim številom.
Naloga 3. Poiščite največji linearno neodvisen podsistem in izračunajte rang sistema vektorjev
.
rešitev. Zmanjšajmo matriko sistema z EPS na stopničasto trikotno obliko. Za razlago postopka črto s številko matrike, ki jo želimo transformirati, označimo s simbolom . Stolpec za puščico označuje dejanja v vrsticah matrike, ki se pretvarjajo, ki jih je treba izvesti za pridobitev vrstic nove matrike.
.
Očitno sta prva dva stolpca nastale matrike linearno neodvisna, tretji stolpec je njuna linearna kombinacija, četrti pa ni odvisen od prvih dveh. Vektorji 
se imenujejo osnovne. Tvorijo največji linearno neodvisen podsistem sistema , rang sistema pa je tri.
Osnova, koordinate
Naloga 4. Poiščite osnovo in koordinate vektorjev v tej bazi na množici geometrijskih vektorjev, katerih koordinate izpolnjujejo pogoj 
.
rešitev. Množica je ravnina, ki poteka skozi izhodišče. Poljubna baza na ravnini je sestavljena iz dveh nekolinearnih vektorjev. Koordinate vektorjev v izbrani bazi določimo z reševanjem ustreznega sistema linearnih enačb.
Obstaja še en način za rešitev te težave, ko lahko osnovo najdete s pomočjo koordinat.
Koordinate 
prostori niso koordinate na ravnini, saj so povezani z relacijo 
, torej niso neodvisni. Neodvisni spremenljivki in (imenujemo jih prosti) enolično določata vektor na ravnini in ju je zato mogoče izbrati kot koordinate v . Nato osnova 
sestoji iz vektorjev, ki ležijo in ustrezajo množicam prostih spremenljivk 
in 
, to je .
Naloga 5. Poiščite bazo in koordinate vektorjev v tej bazi na množici vseh vektorjev v prostoru, katerih lihe koordinate so med seboj enake.
rešitev. Izberimo kot v prejšnjem problemu koordinate v prostoru.
Ker 
, nato proste spremenljivke 
enolično določajo vektor iz in so torej koordinate. Ustrezna baza je sestavljena iz vektorjev.
Naloga 6. Poiščite bazo in koordinate vektorjev v tej bazi na množici vseh matrik oblike 
, Kje 
– poljubna števila.
rešitev. Vsako matriko iz je edinstveno mogoče predstaviti v obliki:
Ta relacija je razširitev vektorja iz glede na bazo 
s koordinatami 
.
Naloga 7. Poiščite razsežnost in bazo linearne lupine sistema vektorjev
.
rešitev. Z EPS transformiramo matriko iz koordinat sistemskih vektorjev v stopničasto trikotno obliko.
.
Stolpci 
zadnje matrike so linearno neodvisne, stolpci pa 
linearno izražena skozi njih. Zato vektorji 
tvorijo osnovo 
, In 
.
Komentiraj. Osnova v je izbrana dvoumno. Na primer vektorji 
tvorijo tudi osnovo 
.
