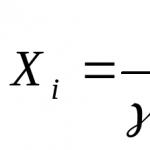Exemplul 1. În prima urnă: trei bile roșii, una albă. În a doua urnă: una roșie, trei bile albe. Se aruncă la întâmplare o monedă: dacă stema este aleasă din prima urnă, în caz contrar, din a doua.
Soluţie:
a) probabilitatea de a extrage o bila rosie
A - am o minge roșie
P 1 - stema a căzut, P 2 - în caz contrar
b) Se alege o bila rosie. Aflați probabilitatea ca acesta să fie luat din prima urnă, din a doua urnă.
B 1 - din prima urna, B 2 - din a doua urna
,
Exemplul 2. Într-o cutie sunt 4 bile. Poate fi: numai alb, doar negru sau alb și negru. (Compoziție necunoscută).
Soluţie:
A este probabilitatea apariției unei bile albe
a) Toți albii:
(probabilitatea ca una dintre cele trei variante în care există alb să fie prinsă)
(probabilitatea ca o minge albă să apară acolo unde toate sunt albe)
b) Scos acolo unde toată lumea este neagră
c) a scos o variantă în care toate sunt albe sau/și negre
- cel putin unul dintre ele este alb
Pa + P b + P c =
Exemplul 3 . O urna contine 5 bile albe si 4 negre. Se scot din el 2 bile la rând. Aflați probabilitatea ca ambele bile să fie albe.
Soluţie:
5 bile albe, 4 negre
P(A 1) - a tras o minge albă
P(A 2) este probabilitatea ca a doua bilă să fie și ea albă
P(A) – Bile albe selectate pe rând
Exemplul 3a. Într-un pachet sunt 2 bancnote contrafăcute și 8 reale. Din pachet au fost scoase la rând 2 bancnote. Găsiți probabilitatea ca ambele să fie false.
Soluţie:
P(2) = 2/10*1/9 = 1/45 = 0,022
Exemplul 4. Sunt 10 urne. 9 urne conțin 2 bile negre și 2 albe. Există 5 albi și 1 negru într-o urnă. Se extrage o minge dintr-o urna luata la intamplare.
Soluţie:
P(A)-? se ia o minge alba dintr-o urna care contine 5 albe
B - probabilitatea de a fi scos din urnă, unde 5 sunt albe
, - scos de la alții
C 1 - probabilitatea apariției unei mingi albe în lvl 9.
C 2 - probabilitatea apariției unei mingi albe, unde sunt 5
P(A 0)= P(B 1) P(C 1)+P(B 2) P(C 2)
Exemplul 5. 20 role cilindrice și 15 conice. Culegătorul ia 1 rolă și apoi altul.
Soluţie:
a) ambele role sunt cilindrice
P(C1)=; P(C2)=
C 1 - primul cilindru, C 2 - al doilea cilindru
P(A)=P(C1)P(C2) =
b) Cel puțin un cilindru
K 1 - primul con.
K 2 - al doilea con.
P(B)=P(C1)P(K2)+P(C2)P(K1)+P(C1)P(C2)
;
c) primul cilindru, iar al doilea nu este
P(C)=P(C1)P(K2)
e) Nici un singur cilindru.
P(D)=P(K 1)P(K 2)
e) Exact 1 cilindru
P(E)=P(C1)P(K2)+P(K1)P(K2)
Exemplul 6. Există 10 piese standard și 5 piese defecte într-o cutie.
Trei piese sunt extrase la întâmplare.
a) Una dintre ele este defectă
P n (K)=C n k p k q n-k ,
P este probabilitatea produselor defecte
q este probabilitatea pieselor standard
n=3, trei părți
b) două din cele trei părți sunt defecte P(2)
c) cel puţin un standard
P(0) - nu este defect
P=P(0)+ P(1)+ P(2) - probabilitatea ca cel puțin o parte să fie standard
Exemplul 7 . Prima urna contine 3 bile albe si 3 negre, iar a 2-a urna contine 3 albe si 4 negre. Se transferă 2 bile din prima urnă în a 2-a urnă fără să se uite, apoi se extrag 2 bile din a 2-a urna. Care este probabilitatea ca ei Culori diferite?
Soluţie:
La transferul bilelor din prima urna sunt posibile urmatoarele optiuni:
a) Se desenează 2 bile albe pe rând
P WB 1 =
Va fi întotdeauna o minge mai puțin în a doua etapă, deoarece o minge a fost deja scoasă în prima etapă.
b) se extrage o bilă albă și una neagră
Situația când a fost extrasă prima bila albă, apoi cea neagră
P BC =
Situația când a fost extrasă prima bila neagră, apoi cea albă
P BW =
Total: P CU 1 =
c) Se desenează 2 bile negre pe rând
P HH 1 =
Deoarece 2 bile au fost transferate din prima urna in a doua urna, numarul total de bile din a doua urna va fi de 9 (7 + 2). În consecință, vom căuta toate opțiunile posibile:
a) Mai întâi se extrage o bilă albă și apoi o bilă neagră din a doua urnă
P BC 2 P BB 1 - înseamnă probabilitatea ca mai întâi să fi fost extrasă o bilă albă, apoi o bilă neagră, cu condiția ca 2 bile albe să fie extrase din prima urnă la rând. De aceea, numărul de bile albe în acest caz este 5 (3+2).
P BC 2 P BC 1 - înseamnă probabilitatea ca o bilă albă să fi fost extrasă mai întâi, apoi o bilă neagră, cu condiția ca din prima urnă să fie extrase bile albe și negre. De aceea, numărul de bile albe în acest caz este 4 (3+1), iar numărul de bile negre este de cinci (4+1).
P BC 2 P BC 1 - înseamnă probabilitatea ca mai întâi să fi fost scoasă o bilă albă, apoi o bilă neagră, cu condiția ca ambele bile negre să fie scoase din prima urna la rând. De aceea, numărul de bile negre în acest caz este 6 (4+2).
Probabilitatea ca cele 2 bile extrase să fie de culori diferite este egală cu:
Răspuns: P = 0,54
Exemplul 7a. Din prima urnă, care conține 5 bile albe și 3 negre, 2 bile sunt transferate aleatoriu în a 2-a urna, care conține 2 bile albe și 6 negre. Apoi 1 minge este extrasă la întâmplare din a 2-a urna.
1) Care este probabilitatea ca mingea extrasă din urna 2 să fie albă?
2) Bila extrasă din a 2-a urnă s-a dovedit a fi albă. Calculați probabilitatea ca bilele să fi fost transferate din urna 1 în urna 2. culoare diferita.
Soluţie.
1) Evenimentul A - mingea extrasă din a 2-a urnă s-a dovedit a fi albă. Luați în considerare următoarele opțiuni pentru apariția acestui eveniment.
a) Două bile albe sunt plasate din prima urnă în a doua: P1(bb) = 5/8*4/7 = 20/56.
În a doua urnă sunt 4 bile albe. Atunci probabilitatea de a extrage o minge albă din a doua urnă este P2(4) = 20/56*(2+2)/(6+2) = 80/448
b) Bilele albe și negre sunt plasate din prima urnă în a doua: P1(bc) = 5/8*3/7+3/8*5/7 = 30/56.
În a doua urnă sunt 3 bile albe. Atunci probabilitatea de a extrage o minge albă din a doua urnă este P2(3) = 30/56*(2+1)/(6+2) = 90/448
c) Două bile negre sunt plasate din prima urna în a doua: P1(hh) = 3/8*2/7 = 6/56.
În a doua urnă sunt 2 bile albe. Atunci probabilitatea de a extrage o minge albă din a doua urnă este P2(2) = 6/56*2/(6+2) = 12/448
Atunci probabilitatea ca mingea extrasă din a 2-a urna să se dovedească a fi albă este egală cu:
P(A) = 80/448 + 90/448 + 12/448 = 13/32
2) Bila extrasă din a 2-a urnă s-a dovedit a fi albă, adică. probabilitatea totală este P(A)=13/32.
Probabilitatea ca bile de diferite culori (alb-negru) să fie transferate în a doua urnă și s-a ales alb: P2(3) = 30/56*(2+1)/(6+2) = 90/448
P = P2(3)/ P(A) = 90/448 / 13/32 = 45/91
Exemplul 7b. Prima urna contine 8 bile albe si 3 negre, a doua urna contine 5 albe si 3 negre. O minge este aleasă la întâmplare din prima și două bile din a doua. După aceea, o minge este luată la întâmplare din cele trei bile alese. Această ultimă minge s-a dovedit a fi neagră. Găsiți probabilitatea ca o minge albă să fi fost aleasă din prima urna.
Soluţie.
Să luăm în considerare toate variantele evenimentului A – din trei bile, bila extrasă s-a dovedit a fi neagră. Cum s-a putut întâmpla ca printre cele trei bile să fie negru?
a) Din prima urna se extrage o bila neagra, iar din a doua urna se extrag doua bile albe.
P1 = (3/11)(5/8*4/7) = 15/154
b) Din prima urna se extrage o bila neagra, iar din a doua urna se extrag doua bile negre.
P2 = (3/11)(3/8*2/7) = 9/308
c) Din prima urna se extrage o bila neagra, iar din a doua urna se extrage o bila alba si una neagra.
P3 = (3/11)(3/8*5/7+5/8*3/7) = 45/308
d) Din prima urna se extrage o bila alba, iar din a doua urna se iau doua bile negre.
P4 = (8/11)(3/8*2/7) = 6/77
e) Din prima urna s-a scos o bila alba, iar din a doua urna s-a scos o bila alba si una neagra.
P5 = (8/11)(3/8*5/7+5/8*3/7) = 30/77
Probabilitatea totală este: P = P1+P2+ P3+P4+P5 = 15/154+9/308+45/308+6/77+30/77 = 57/77
Probabilitatea ca o minge albă să fi fost aleasă dintr-o urna albă este:
Pb(1) = P4 + P5 = 6/77+30/77 = 36/77
Atunci probabilitatea ca o bilă albă să fi fost aleasă din prima urna, cu condiția ca una neagră să fi fost aleasă dintre trei bile, este egală cu:
Pch \u003d Pb (1) / P \u003d 36/77 / 57/77 \u003d 36/57
Exemplul 7c. Prima urna contine 12 bile albe si 16 negre, a doua urna contine 8 albe si 10 negre. În același timp, se scoate câte o minge din urna 1 și 2, se amestecă și se întoarce pe rând în fiecare urnă. Apoi se extrage o minge din fiecare urna. S-au dovedit a fi de aceeași culoare. Determinați probabilitatea ca în prima urnă să rămână tot atâtea bile albe câte erau la început.
Soluţie.
Evenimentul A - în același timp, se extrage o minge din prima și a doua urnă.
Probabilitatea extragerii unei bile albe din prima urna: P1(B) = 12/(12+16) = 12/28 = 3/7
Probabilitatea extragerii unei bile negre din prima urna: P1(H) = 16/(12+16) = 16/28 = 4/7
Probabilitatea de a extrage o minge albă din a doua urnă: P2(B) = 8/18 = 4/9
Probabilitatea de a extrage o minge neagră din a doua urnă: P2(H) = 10/18 = 5/9
S-a întâmplat evenimentul A. Evenimentul B - se extrage o minge din fiecare urna. După amestecare, probabilitatea de a întoarce mingea în urna unei bile albe sau negre este de ½.
Luați în considerare variantele evenimentului B - s-au dovedit a fi de aceeași culoare.
Pentru prima urnă
1) a fost plasată o bilă albă în prima urnă și a fost extrasă una albă, cu condiția ca în prealabil să fi fost extrasă o bilă albă, P1(BB/A=B) = ½ * 12/28 * 3/7 = 9/98
2) a fost plasată o bilă albă în prima urnă și a fost extrasă o bilă albă, cu condiția ca o bilă neagră să fi fost extrasă mai devreme, P1(BB/A=W) = ½ * 13/28 * 4/7 = 13/98
3) a fost plasată o bilă albă în prima urnă și a fost extrasă una neagră, cu condiția ca în prealabil să fi fost extrasă o bilă albă, P1(BC/A=B) = ½ * 16/28 * 3/7 = 6/49
4) a fost plasată o bilă albă în prima urnă și a fost extrasă una neagră, cu condiția ca o bilă neagră să fie extrasă mai devreme, P1(BC/A=Ch) = ½ * 15/28 * 4/7 = 15/98
5) a fost plasată o bilă neagră în prima urnă și a fost extrasă o bilă albă, cu condiția ca în prealabil să fi fost extrasă o bilă albă, P1(BW/A=B) = ½ * 11/28 * 3/7 = 33/392
6) a fost plasată o bilă neagră în prima urnă și a fost extrasă una albă, cu condiția ca în prealabil să fi fost extrasă o bilă neagră, P1(BW/A=W) = ½ * 12/28 * 4/7 = 6/49
7) a fost plasată o bilă neagră în prima urnă și a fost extrasă una neagră, cu condiția ca în prealabil să fi fost extrasă o bilă albă, P1(HH/A=B) = ½ * 17/28 * 3/7 = 51/392
8) a fost plasată o bilă neagră în prima urnă și a fost extrasă una neagră, cu condiția ca o bilă neagră să fie extrasă mai devreme, P1(HH/A=H) = ½ * 16/28 * 4/7 = 8/49
Pentru a doua urnă
1) a fost plasată o bilă albă în prima urnă și a fost extrasă una albă, cu condiția ca în prealabil să fi fost extrasă o bilă albă, P1(BB/A=B) = ½ * 8/18 * 3/7 = 2/21
2) a fost plasată o bilă albă în prima urnă și a fost extrasă o bilă albă, cu condiția ca o bilă neagră să fie extrasă mai devreme, P1(BB/A=W) = ½ * 9/18 * 4/7 = 1/7
3) a fost plasată o bilă albă în prima urnă și a fost extrasă una neagră, cu condiția ca o bilă albă să fie extrasă mai devreme, P1(BC/A=B) = ½ * 10/18 * 3/7 = 5/42
4) a fost plasată o bilă albă în prima urnă și a fost extrasă una neagră, cu condiția ca o bilă neagră să fie extrasă mai devreme, P1(BC/A=Ch) = ½ * 9/18 * 4/7 = 1/7
5) a fost plasată o bilă neagră în prima urnă și a fost extrasă o bilă albă, cu condiția ca în prealabil să fi fost extrasă o bilă albă, P1(BW/A=B) = ½ * 7/18 * 3/7 = 1/12
6) a fost plasată o bilă neagră în prima urnă și a fost extrasă una albă, cu condiția ca în prealabil să fi fost extrasă o bilă neagră, P1(BW/A=W) = ½ * 8/18 * 4/7 = 8/63
7) a fost plasată o bilă neagră în prima urnă și a fost extrasă una neagră, cu condiția ca în prealabil să fi fost extrasă o bilă albă, P1(HH/A=B) = ½ * 11/18 * 3/7 = 11/84
8) a fost plasată o bilă neagră în prima urnă și a fost extrasă una neagră, cu condiția ca o bilă neagră să fie extrasă mai devreme, P1(HH/A=H) = ½ * 10/18 * 4/7 = 10/63
Bilele s-au dovedit a fi de aceeași culoare:
un alb
P1(B) = P1(BB/A=B) + P1(BB/A=B) + P1(BW/A=B) + P1(BW/A=B) = 9/98 + 13/98 + 33 /392 + 6/49 = 169/392
P2(B) = P1(BB/A=B) + P1(BB/A=B) + P1(BW/A=B) + P1(BW/A=B) = 2/21+1/7+1 /12+8/63 = 113/252
b) negru
P1(H) = P1(BH/A=B) + P1(BH/A=B) + P1(BH/A=B) + P1(BH/A=B) = 6/49 + 15/98 + 51 /392 + 8/49 = 223/392
P2(H) = P1(WB/A=B) + P1(BH/A=B) + P1(BH/A=B) + P1(BH/A=B) =5/42+1/7+11 /84+10/63 = 139/252
P = P1(B)* P2(B) + P1(H)* P2(H) = 169/392*113/252 + 223/392*139/252 = 5/42
Exemplul 7g. Prima cutie conține 5 bile albe și 4 albastre, a doua 3 și 1, iar a treia 4 și, respectiv, 5. O cutie este aleasă la întâmplare și o minge extrasă din ea se dovedește a fi albastră. Care este probabilitatea ca această minge să fie din a doua cutie?
Soluţie.
A - eveniment de extracție a balonului albastru. Luați în considerare toate opțiunile pentru rezultatul unui astfel de eveniment.
H1 - minge extrasă din prima casetă,
H2 - minge extrasă din a doua casetă,
H3 - mingea extrasă din a treia casetă.
P(H1) = P(H2) = P(H3) = 1/3
În funcție de starea problemei, probabilitățile condiționate ale evenimentului A sunt:
P(A|H1) = 4/(5+4) = 4/9
P(A|H2) = 1/(3+1) = 1/4
P(A|H3) = 5/(4+5) = 5/9
P(A) = P(H1)*P(A|H1) + P(H2)*P(A|H2) + P(H3)*P(A|H3) = 1/3*4/9 + 1 /3*1/4 + 1/3*5/9 = 5/12
Probabilitatea ca această minge să fie din a doua casetă este:
P2 = P(H2)*P(A|H2) / P(A) = 1/3*1/4 / 5/12 = 1/5 = 0,2
Exemplul 8 . Cinci cutii cu 30 de bile fiecare conțin 5 bile roșii (aceasta este cutia de compoziție H1), alte șase cutii cu 20 de bile fiecare conțin 4 bile roșii (aceasta este cutia de compoziție H2). Găsiți probabilitatea ca o bilă roșie extrasă aleatoriu să fie conținută într-una dintre primele cinci casete.
Soluție: Sarcina aplicării formulei probabilitate deplină.
P(H1) = 5/11
Probabilitatea ca orice Mingea luată este conținută într-una din cele șase cutii:
P(H2) = 6/11
Evenimentul a avut loc - a fost extrasă o minge roșie. Prin urmare, acest lucru se poate întâmpla în două cazuri:
a) scos din primele cinci cutii.
P 5 = 5 bile roșii * 5 cutii / (30 bile * 5 cutii) = 1/6
P(P 5 / H 1) \u003d 1/6 * 5/11 \u003d 5/66
b) scos din alte șase cutii.
P 6 = 4 bile roșii * 6 cutii / (20 bile * 6 cutii) = 1/5
P (P 6 / H 2) \u003d 1/5 * 6/11 \u003d 6/55
Total: P(P 5 /H 1) + P(P 6 /H 2) = 5/66 + 6/55 = 61/330
Prin urmare, probabilitatea ca o minge roșie extrasă aleatoriu să fie conținută într-una dintre primele cinci casete este:
P k.sh. (H1) = P(P 5 /H 1) / (P(P 5 /H 1) + P(P 6 /H 2)) = 5/66 / 61/330 = 25/61
Exemplul 9 . O urnă conține 2 bile albe, 3 negre și 4 roșii. Trei bile sunt extrase la întâmplare. Care este probabilitatea ca cel puțin două bile să fie de aceeași culoare?
Soluţie. Există trei posibile rezultate ale evenimentelor:
a) dintre cele trei bile extrase, cel puțin două sunt albe.
P b (2) = P 2b
Numărul total de rezultate elementare posibile pentru aceste încercări este egal cu numărul de moduri în care pot fi extrase 3 bile din 9:
Aflați probabilitatea ca 2 din cele 3 bile să fie albe.
Numărul de opțiuni de a alege dintre 2 bile albe:
Numărul de opțiuni de a alege din alte 7 bile a treia bilă:
b) dintre cele trei bile extrase, cel puțin două sunt negre (adică fie 2 negre, fie 3 negre).
Aflați probabilitatea ca 2 din cele 3 bile să fie negre.
Numărul de opțiuni de a alege dintre 3 bile negre:
Numărul de opțiuni de a alege din alte 6 bile dintr-o singură minge:
P2h = 0,214
Găsiți probabilitatea ca toate bilele alese să fie negre.
P h (2) = 0,214+0,0119 = 0,2259
c) dintre cele trei bile extrase, cel puțin două sunt roșii (adică fie 2 roșii, fie 3 roșii).
Să aflăm probabilitatea ca dintre cele 3 bile alese 2 să fie roșii.
Numărul de opțiuni de a alege dintre 4 bile negre:
Numărul de opțiuni de a alege dintre 5 bile albe rămase 1 albă:
Găsiți probabilitatea ca toate bilele alese să fie roșii.
P la (2) = 0,357 + 0,0476 = 0,4046
Atunci probabilitatea ca cel puțin două bile să fie de aceeași culoare este: P = P b (2) + P h (2) + P c (2) = 0,0833 + 0,2259 + 0,4046 = 0,7138
Exemplul 10 . Prima urna contine 10 bile, dintre care 7 sunt albe; A doua urnă conține 20 de bile, dintre care 5 sunt albe. Din fiecare urnă se extrage o minge la întâmplare, apoi se extrage o minge la întâmplare din aceste două bile. Găsiți probabilitatea ca o bilă albă să fie extrasă.
Soluţie. Probabilitatea ca o minge albă să fi fost extrasă din prima urnă este P(b)1 = 7/10. În consecință, probabilitatea de a extrage o bilă neagră este P(h)1 = 3/10.
Probabilitatea ca o minge albă să fie extrasă din a doua urnă este P(b)2 = 5/20 = 1/4. În consecință, probabilitatea de a extrage o bilă neagră este P(h)2 = 15/20 = 3/4.
Evenimentul A - o bilă albă este luată din două bile
Luați în considerare rezultatul evenimentului A.
- Din prima urna se extrage o bila alba, iar din a doua urna se extrage o bila alba. Apoi a fost extrasă o minge albă din aceste două bile. P1=7/10*1/4=7/40
- Din prima urna se extrage o bila alba, iar din a doua urna se extrage o bila neagra. Apoi a fost extrasă o minge albă din aceste două bile. P2 = 7/10*3/4 = 21/40
- Din prima urna se extrage o bila neagra, iar din a doua urna se extrage o bila alba. Apoi a fost extrasă o minge albă din aceste două bile. P3=3/10*1/4=3/40
P = P1 + P2 + P3 = 7/40 + 21/40 + 3/40 = 31/40
Exemplul 11 . Există n mingi de tenis într-o cutie. Dintre ei au jucat m . Pentru primul joc, au luat două mingi la întâmplare și le-au pus înapoi după joc. Pentru al doilea joc au luat și două mingi la întâmplare. Care este probabilitatea ca al doilea joc să fie jucat cu mingi noi?
Soluţie. Luați în considerare evenimentul A - jocul a fost jucat pentru a doua oară cu mingi noi. Să vedem ce evenimente pot duce la asta.
Notați cu g = n-m, numărul de bile noi înainte de a le scoate.
a) Sunt extrase două mingi noi pentru primul joc.
P1 = g/n*(g-1)/(n-1) = g(g-1)/(n(n-1))
b) pentru primul joc au scos o minge nouă și una deja jucată.
P2 = g/n*m/(n-1) + m/n*g/(n-1) = 2mg/(n(n-1))
c) pentru primul joc au fost scoase două mingi jucate.
P3 = m/n*(m-1)/(n-1) = m(m-1)/(n(n-1))
Luați în considerare evenimentele celui de-al doilea joc.
a) Au fost extrase două bile noi, cu condiția P1: deoarece bile noi au fost deja extrase pentru primul joc, apoi pentru al doilea joc numărul lor a scăzut cu 2, g-2.
P(A/P1) = (g-2)/n*(g-2-1)/(n-1)*P1 = (g-2)/n*(g-2-1)/(n- 1)*g(g-1)/(n(n-1))
b) Au fost extrase două bile noi, sub rezerva P2: deoarece o bilă nouă a fost deja extrasă pentru primul joc, apoi pentru al doilea joc numărul lor a scăzut cu 1, g-1.
P(A/P2) =(g-1)/n*(g-2)/(n-1)*P2 = (g-1)/n*(g-2)/(n-1)*2mg /(n(n-1))
c) Au scos două bile noi, cu condiția P3: deoarece nu au fost folosite bile noi pentru primul joc, numărul lor nu s-a schimbat pentru al doilea joc g.
P(A/P3) = g/n*(g-1)/(n-1)*P3 = g/n*(g-1)/(n-1)*m(m-1)/(n (n-1))
Probabilitate totală P(A) = P(A/P1) + P(A/P2) + P(A/P3) = (g-2)/n*(g-2-1)/(n-1)* g(g-1)/(n(n-1)) + (g-1)/n*(g-2)/(n-1)*2mg/(n(n-1)) + g/n *(g-1)/(n-1)*m(m-1)/(n(n-1)) = (n-2)(n-3)(n-m-1)(n-m)/(( n-1)^2*n^2)
Răspuns: P(A)=(n-2)(n-3)(n-m-1)(n-m)/((n-1)^2*n^2)
Exemplul 12 . Prima, a doua și a treia cutie conțin 2 bile albe și 3 negre fiecare, a patra și a cincea cutie conțin fiecare 1 bile albă și 1 neagră. O cutie este aleasă aleatoriu și din ea se extrage o minge. Care este probabilitatea condiționată ca a patra sau a cincea casetă să fie selectată dacă mingea extrasă este albă?
Soluţie.
Probabilitatea de a alege fiecare casetă este P(H) = 1/5.
Luați în considerare probabilitățile condiționate ale evenimentului A - tragerea unei mingi albe.
P(A|H=1) = 2/5
P(A|H=2) = 2/5
P(A|H=3) = 2/5
P(A|H=4) = ½
P(A|H=5) = ½
Probabilitatea totală de a extrage o minge albă:
P(A) = 2/5*1/5 + 2/5*1/5 +2/5*1/5 +1/2*1/5 +1/2*1/5 = 0,44
Probabilitatea condiționată ca a patra casetă să fie selectată
P(H=4|A) = 1/2*1/5 / 0,44 = 0,2273
Probabilitate condiționată ca a cincea casetă să fie selectată
P(H=5|A) = 1/2*1/5 / 0,44 = 0,2273
Deci, probabilitatea condiționată ca a patra sau a cincea casetă să fie aleasă este
P(H=4, H=5|A) = 0,2273 + 0,2273 = 0,4546
Exemplul 13 . O urnă conține 7 bile albe și 4 roșii. Apoi se punea o altă minge de culoare albă sau roșie sau neagră în urnă și după amestecare se scotea o minge. S-a dovedit a fi roșu. Care este probabilitatea ca a) să fi fost plasată o minge roșie? b) bila neagra?
Soluţie.
a) bila rosie
Evenimentul A - este extrasă o minge roșie. Evenimentul H - puneți o minge roșie. Probabilitatea ca o minge roșie să fi fost plasată în urnă P(H=K) = 1 / 3
Atunci P(A|H=K)= 1 / 3 * 5 / 12 = 5 / 36 = 0,139
b) bila neagră
Evenimentul A - este extrasă o minge roșie. Evenimentul H - puneți o minge neagră.
Probabilitatea ca o bilă neagră să fi fost plasată în urnă este P(H=H) = 1/3
Atunci P(A|H=H)= 1 / 3 * 4 / 12 = 1 / 9 = 0,111
Exemplul 14 . Sunt două urne cu bile. Unul are 10 bile roșii și 5 albastre, celălalt are 5 bile roșii și 7 albastre. Care este probabilitatea ca o bila rosie sa fie extrasa la intamplare din prima urna si una albastra din a doua?
Soluţie. Fie evenimentul A1 - se extrage o bila rosie din prima urna; A2 - se extrage o bila albastra din a doua urna:
,
Evenimentele A1 și A2 sunt independente. Probabilitatea de apariție în comun a evenimentelor A1 și A2 este egală cu
Exemplul 15 . Există un pachet de cărți (36 de piese). Două cărți sunt extrase la întâmplare. Care este probabilitatea ca ambele cărți extrase să fie roșii?
Soluţie. Fie evenimentul A 1 să fie prima carte extrasă din culoarea roșie. Evenimentul A 2 - a doua carte extrasă a costumului roșu. B - ambele cărți extrase de culoare roșie. Deoarece atât evenimentul A 1 cât și evenimentul A 2 trebuie să aibă loc, atunci B = A 1 · A 2 . Evenimentele A1 și A2 sunt dependente, deci P(B):
,
De aici
Exemplul 16 . Două urne conțin bile care diferă doar prin culoare, iar în prima urnă sunt 5 bile albe, 11 negre și 8 roșii, iar în a doua 10, 8, respectiv 6 bile. Din ambele urne se extrage o minge la întâmplare. Care este probabilitatea ca ambele bile să aibă aceeași culoare?
Soluţie. Fie ca indicele 1 să însemne culoare alba, indice 2 - culoare neagră; 3 - culoare roșie. Fie evenimentul A i - din prima urna se extrage o bila de culoarea i-a; evenimentul B j - o minge de j -a culoare a fost luată din a doua urnă; evenimentul A - ambele bile sunt de aceeași culoare.
A \u003d A 1 B 1 + A 2 B 2 + A 3 B 3. Evenimentele A i și B j sunt independente, în timp ce A i · B i și A j · B j sunt incompatibile pentru i ≠ j . Prin urmare,
P(A)=P(A 1) P(B 1)+P(A 2) P(B 2)+P(A 3) P(B 3) =
Exemplul 17 . Dintr-o urna cu 3 bile albe si 2 negre se extrag una cate una pana apare negru. Care este probabilitatea ca 3 bile să fie extrase din urnă? 5 bile?
Soluţie.
1) probabilitatea ca 3 bile să fie extrase din urnă (adică a treia bilă va fi neagră, iar primele două vor fi albe).
P=3/5*2/4*2/3=1/5
2) probabilitatea ca 5 bile să fie extrase din urnă
o astfel de situaţie nu este posibilă, pentru că doar 3 bile albe.
P=0
Corolarul ambelor teoreme principale - teorema de adunare a probabilității și teorema de înmulțire a probabilității - este așa-numita formulă a probabilității totale.
Să fie necesar să se determine probabilitatea unui eveniment care poate apărea împreună cu unul dintre evenimentele:
formând un grup complet de evenimente incompatibile. Vom numi aceste evenimente ipoteze.
Să demonstrăm că în acest caz
 , (3.4.1)
, (3.4.1)
acestea. probabilitatea unui eveniment se calculează ca suma produselor dintre probabilitatea fiecărei ipoteze și probabilitatea evenimentului conform acestei ipoteze.
Formula (3.4.1) se numește formula probabilității totale.
Dovada. Deoarece ipotezele formează un grup complet, evenimentul poate apărea numai în combinație cu oricare dintre aceste ipoteze:
Deoarece ipotezele sunt inconsistente, combinațiile ![]() de asemenea incompatibil; aplicându-le teorema adunării, obținem:
de asemenea incompatibil; aplicându-le teorema adunării, obținem:
Aplicând teorema înmulțirii evenimentului, obținem:
 ,
,
Q.E.D.
Exemplul 1. Există trei urne cu aspect identic; prima urnă conține două bile albe și una neagră; în al doilea - trei albi și unul negru; în al treilea - două bile albe și două negre. Cineva alege una dintre urne la întâmplare și trage o minge din ea. Găsiți probabilitatea ca această minge să fie albă.
Soluţie. Să luăm în considerare trei ipoteze:
Alegerea primei urne,
Alegerea celei de-a doua urne,
Alegerea celei de-a treia urne
iar evenimentul este apariția unei mingi albe.
Întrucât ipotezele, după starea problemei, sunt la fel de probabile, atunci
![]() .
.
Probabilitățile condiționate ale evenimentului conform acestor ipoteze sunt, respectiv, egale:
Conform formulei probabilității totale
![]() .
.
Exemplul 2. Trei focuri simple sunt trase într-o aeronavă. Probabilitatea de a lovi cu prima lovitură este de 0,4, cu a doua - 0,5, cu a treia 0,7. Trei lovituri sunt, evident, suficiente pentru a dezactiva o aeronavă; cu o lovitură, aeronava eșuează cu o probabilitate de 0,2, cu două lovituri, cu o probabilitate de 0,6. Găsiți probabilitatea ca, în urma a trei lovituri, aeronava să fie scoasă din funcțiune.
Soluţie. Să luăm în considerare patru ipoteze:
Nici un obuz nu a lovit avionul,
Un obuz a lovit avionul
Avionul a fost lovit de două obuze.
Trei obuze au lovit avionul.
Folosind teoremele de adunare și înmulțire, găsim probabilitățile acestor ipoteze:

Probabilitățile condiționate ale evenimentului (defecțiunea aeronavei) conform acestor ipoteze sunt:
Aplicând formula probabilității totale, obținem:
Rețineți că prima ipoteză nu ar fi putut fi introdusă în considerare, deoarece termenul corespunzător din formula probabilității totale dispare. Acest lucru se face de obicei atunci când se aplică formula probabilității totale, luând în considerare nu grupul complet de ipoteze inconsecvente, ci doar pe acelea dintre ele sub care un anumit eveniment este posibil.
Exemplul 3. Funcționarea motorului este controlată de două regulatoare. Se are în vedere o anumită perioadă de timp, în care este de dorit să se asigure funcționarea fără probleme a motorului. Dacă ambele regulatoare sunt prezente, motorul se defectează cu probabilitate, dacă doar primul dintre ele funcționează, cu probabilitate, dacă funcționează doar al doilea, dacă ambele regulatoare se defectează, cu probabilitate. Primul dintre reglementatori are fiabilitate, al doilea -. Toate elementele eșuează independent unele de altele. Găsiți fiabilitatea totală (probabilitatea de funcționare fără defecțiuni) a motorului.
Considera eveniment dependent, care poate apărea doar ca urmare a implementării unuia dintre incompatibile ipoteze
![]() , care formează grup complet. Fie cunoscute probabilitățile lor și probabilitățile condiționate corespunzătoare. Atunci probabilitatea producerii evenimentului este:
, care formează grup complet. Fie cunoscute probabilitățile lor și probabilitățile condiționate corespunzătoare. Atunci probabilitatea producerii evenimentului este:
Această formulă se numește formule de probabilitate totală. În manuale, ea este formulată printr-o teoremă a cărei demonstrație este elementară: conform algebra evenimentelor, (evenimentul a avut loc Și sau s-a întâmplat un eveniment Și după ce a venit evenimentul sau s-a întâmplat un eveniment Și după ce a venit evenimentul sau …. sau s-a întâmplat un eveniment Și eveniment urmat). Din moment ce ipotezele ![]() sunt incompatibile, iar evenimentul este dependent teorema de adunare pentru probabilitățile evenimentelor incompatibile (primul pas)Și teorema înmulțirii probabilităților evenimente dependente
(al doilea pas):
sunt incompatibile, iar evenimentul este dependent teorema de adunare pentru probabilitățile evenimentelor incompatibile (primul pas)Și teorema înmulțirii probabilităților evenimente dependente
(al doilea pas):

Sarcina 1
Sunt trei urne identice. Prima urnă conține 4 bile albe și 7 negre, a doua urnă conține doar bile albe, iar a treia urnă conține doar bile negre. O urna este aleasa la intamplare si se extrage o minge din ea la intamplare. Care este probabilitatea ca această minge să fie neagră?
Soluţie: luați în considerare evenimentul - o bilă neagră va fi extrasă dintr-o urna aleasă aleatoriu. Acest eveniment poate apărea ca urmare a implementării uneia dintre următoarele ipoteze:
– se va selecta prima urna;
– se va alege a 2-a urna;
– se va alege a 3-a urna.
Deoarece urna este aleasă la întâmplare, alegerea oricăreia dintre cele trei urne la fel de posibil, prin urmare: ![]()
Rețineți că se formează ipotezele de mai sus grup complet de evenimente, adică, în funcție de condiție, o minge neagră poate apărea doar din aceste urne și, de exemplu, nu zbura de la o masă de biliard. Să facem o verificare intermediară simplă: ![]() OK, hai sa mergem mai departe:
OK, hai sa mergem mai departe:
Prima urna contine 4 albe + 7 negre = 11 bile, fiecare definiție clasică:
este probabilitatea de a extrage o bilă neagră dat fiind că se va alege prima urnă.
A doua urnă conține doar bile albe, deci dacă este ales aspectul unei bile negre devine imposibil: .
Și, în sfârșit, în a treia urnă sunt doar bile negre, ceea ce înseamnă că corespunzătoare probabilitate condițională extragerea bilei negre va fi (evenimentul este sigur).
Conform formulei probabilității totale:
este probabilitatea ca o bilă neagră să fie extrasă dintr-o urna aleasă aleatoriu.
Răspuns:
Sarcina 2
Există 5 puști diferite în poligonul de tragere. Probabilitățile de a lovi ținta pentru un anumit trăgător sunt, respectiv, egale cu ![]() și 0,4. Care este probabilitatea de a lovi ținta dacă trăgătorul trage o lovitură dintr-o pușcă aleasă aleatoriu?
și 0,4. Care este probabilitatea de a lovi ținta dacă trăgătorul trage o lovitură dintr-o pușcă aleasă aleatoriu?
Sarcina 3
Există 5 puști în piramidă, dintre care trei sunt echipate cu o vizor optic. Probabilitatea ca trăgătorul să lovească ținta atunci când este tras de la o pușcă cu o vizor telescopic este de 0,95; pentru pușcă fără vizor optic această probabilitate este de 0,7. Găsiți probabilitatea ca ținta să fie lovită dacă trăgătorul trage o lovitură dintr-o pușcă luată la întâmplare.
Soluţie: în această problemă, numărul de puști este exact același ca în cea precedentă, dar există doar două ipoteze:
- trăgătorul va alege o pușcă cu vizor optic;
- trăgătorul va selecta o pușcă fără o vizor telescopic.
De definiția clasică a probabilității: ![]() .
.
Control:
Sarcina 4
Motorul funcționează în trei moduri: normal, forțat și ralanti. În modul inactiv, probabilitatea eșecului său este de 0,05, în modul normal - 0,1 și în modul forțat - 0,7. 70% din timp motorul funcționează în modul normal și 20% în modul forțat. Care este probabilitatea defecțiunii motorului în timpul funcționării?
Există trei urne cu aspect identic; prima urna contine 2 bile albe si 1 neagra; in a doua urna sunt 3 bile albe si 1 neagra; in al treilea sunt 2 bile albe si 2 negre.
Cineva alege una dintre urne la întâmplare și trage o minge din ea. Găsiți probabilitatea ca această minge să fie albă.
Să luăm în considerare trei ipoteze:
H1-selectarea primei urne
H2-selectarea celei de-a doua urne
H3-selectarea celei de-a treia urne
un grup complet de evenimente incompatibile.
Fie evenimentul A aspectul unei mingi albe. Deoarece ipotezele, în funcție de condiția problemei sunt la fel de posibile, atunci Р(Н1) = Р(Н2) = Р(Н3) = 1\3
Probabilitățile condiționate ale evenimentului A în aceste ipoteze sunt, respectiv, egale: Р(А/Н1) =2\3; P(A/H2) = 3\4; P (A / H3) \u003d 1/2.
Conform formulei probabilității totale
P(A)=1\3*3\2+1\3*3\4+1\3*1\2=23\36
Raspuns: 23/36
P.2. Teorema ipotezei.
O consecință a teoremei înmulțirii și a formulei probabilității totale este așa-numita teoremă de ipoteză sau formula Bayes (Bayes).
Să stabilim următoarea sarcină.
Există un grup complet de ipoteze incompatibile H1, H2,. . Hn. probabilitățile acestor ipoteze anterioare experimentelor sunt cunoscute și, respectiv, egale cu Р(Н1),Р(Н2)…,Р(Нn). S-a făcut un experiment, în urma căruia s-a observat apariția unui eveniment A. Întrebarea este cum ar trebui modificate probabilitățile ipotezelor în legătură cu apariția acestui eveniment?
Aici, în esență, vorbim despre găsirea probabilității condiționate P(H1/A) pentru fiecare ipoteză.
Din teorema înmulțirii avem:
P(A*Hi) =P(A) P(Hi/A) =P(Hi) P(A/Hi), (i=1,2,3, .n) sau, aruncând partea stângă Nutrend enduro bcaa Cumpărați 120 de capsule.
P(A) P(Hi/A) =P(Hi) P(A/Hi),(i=1,2,. .,n)
De unde P (Hi/A) =P(Hi) P(A/Hi) ÷P(A),(i=1,2,3, . . n)
Exprimând cu P(A) folosind probabilitatea totală, avem
P(Hi/A) =P(Hi) P(A/Hi) ÷∑P(Hi) P(A\Hi),(i=1,2,3, . . n) (2)
Formula (2) se numește formula Bays sau teorema ipotezei
Exemplul 2. Într-o fabrică, 30% din produse sunt produse de mașina I, 25% din produse sunt produse de mașina II, restul de produse sunt produse de mașina III. Pentru mașina I, 1% din producția sa este defectă, pentru mașina II - 1,5%, pentru mașina III - 2%, o unitate de producție aleasă aleatoriu s-a dovedit a fi un defect. Care este probabilitatea ca acesta să fi fost produs de mașina I?
Să introducem notația pentru evenimente.
A - produsul selectat sa dovedit a fi defect
H1-produs produs de mașina I
H2 - produs produs de mașina II
H3 - produs produs de mașina III
P(H1)=0,30; P(H2)=0,25; P(H3) = 0,45
P (A / H1) \u003d 0,01,
P (A / H2) \u003d 0,015
P (A / H3) \u003d 0,02
P(A) \u003d 0,01 * 0,30 + 0,015 * 0,25 + 0,02 * 0,45 \u003d 0,015,
P(H1/A) = 0,01*0,30÷0,015=0,20
Răspuns: 20% din toate produsele defecte sunt produse de mașina I.
§9. formula Bernoulli
Lege numere mari
Fie A eveniment aleatoriu cu privire la o anumită experiență σ. Ne va interesa doar dacă evenimentul A s-a produs sau nu în urma experimentului, așa că vom lua următorul punct de vedere: spațiul evenimentelor elementare asociate experienței σ este format din doar două elemente - A și A. Să notăm probabilitățile acestor elemente, respectiv, prin p și q , (p+q=1).
Să presupunem acum că experimentul σ în condiții neschimbate se repetă de un anumit număr de ori, de exemplu, de 3 ori. Să fim de acord să considerăm realizarea triplă a lui σ ca un anumit experienta nouaη. Dacă, ca și înainte, ne interesează doar apariția sau neapariția lui A., atunci ar trebui în mod evident să presupunem că spațiul evenimentelor elementare corespunzător experimentului η este format din toate secvențele posibile de lungime 3: (A, A, A), (A, A, A), ( A, A, A), (A, A, A), (A, A, A), (A, A, A), (A, A, A) , (A, A, A), care poate fi compus din A și A.
Fiecare dintre aceste secvențe înseamnă una sau alta secvență de apariție sau neapariție a evenimentelor A în trei experimente σ, de exemplu, secvența (A, A, A) înseamnă că A a avut loc în primul experiment și A a avut loc în al doilea. și al treilea. Să definim ce probabilități ar trebui să fie atribuite fiecăreia dintre secvențele (1)
Condiția ca experimentul σ să fie efectuat de toate trei ori în condiții neschimbate ar trebui să însemne următorul lucru: rezultatul fiecăruia dintre cele trei experimente nu depinde de rezultatele care au avut loc în celelalte două experimente. Acestea. orice combinație a rezultatelor a trei experimente este un triplu de evenimente independente. În acest caz, este firesc să se atribuie unui eveniment elementar (A, A, A) o probabilitate egală cu p*q*q, unui eveniment (A, A, A), probabilitatea q*y*y , etc.
Acea. ajungem la următoarea descriere a modelului probabilistic pentru experimentul η (adică pentru implementarea triplă a experimentului σ). Spațiul Ω al evenimentelor elementare este un set de 2 până la 3 secvențe. (1). Fiecare secvență este asociată ca probabilitate cu numărul p ridicat la puterea k, q ridicat la puterea e, unde exponenții determină de câte ori apar simbolurile A și A în expresia pentru această secvență.
Modelele probabilistice de acest fel sunt numite scheme Bernoulli. În cazul general, schema Bernoulli este determinată de valoarea numerelor n și p, unde n este numărul de repetări ale experimentului inițial σ (în experimentul anterior, am considerat n=3), iar p este probabilitatea a evenimentului A în raport cu experimentul σ.
Teorema 1. Fie probabilitatea unui eveniment A egală cu p, iar Pmn probabilitatea ca într-o serie de n încercări independente acest eveniment să se producă de m ori.
Atunci formula Bernoulli este valabilă.
Pmn=Cn la puterea lui m *P la puterea lui m *q in grade n-m
Moneda este aruncată de 10 ori. Care este probabilitatea ca stema să apară exact de 3 ori?
ÎN acest caz pierderea stemei este considerată un succes, probabilitatea p a acestui eveniment în fiecare experiment este de 1/2.
Prin urmare: Р10,3=С10în gradul 3*(1\2) în gradul 3*(1\2) în gradul 7=10*9*8÷1*2*3*(1÷2în gradul 10 ) =15\128
Răspuns: 15\128
La numere mari teste, frecvența relativă de apariție a unui eveniment diferă puțin de probabilitatea acestui eveniment. Formularea matematică a acestei afirmații calitative este dată de legea numerelor mari a lui Bernoulli, care a fost rafinată de Cebyshev.
Teorema 2. Fie probabilitatea evenimentului A în încercarea p egală cu p și să se realizeze o serie formată din n repetări independente ale acestei încercări.
Notăm cu m numărul de încercări în care a avut loc evenimentul A. Atunci, pentru orice număr pozitiv α, se aplică următoarea inegalitate:
3(|m\n-p|> α) Sensul acestei inegalități este că expresia m÷n este egală cu frecvența relativă a evenimentului A într-o serie de experimente, iar |m\n-p|> α înseamnă că abaterea acestei relative de la valoarea teoretică p. Inegalitatea |m\n-p|> α înseamnă că abaterea este mai mare decât α. Dar la o valoare constantă a lui α, pe măsură ce n crește, partea dreaptă a inegalității (3) tinde spre zero. Cu alte cuvinte, seriile în care abaterea frecvenței experimentale față de cea teoretică este mare constituie o mică parte din toate seriile de teste posibile. Din teorema rezulta afirmatia obtinuta de Bernoulli: in conditiile teoremei, pentru orice valoare a α>0, avem Soluţie. Să notăm evenimentele: A - „articolul selectat este defect”, H i - „articolul selectat primit de la al-lea furnizor”, i =1, 2, 3 Ipotezele H 1 , H 2 , H 3 formează un grup complet de evenimente incompatibile. După condiție Conform formulei probabilității totale (1.11), probabilitatea evenimentului A este egală cu Fie ca evenimentul A să fi avut deja loc în condițiile exemplului anterior: piesa selectată s-a dovedit a fi defectă. Care este probabilitatea ca acesta să fi fost primit de la primul furnizor? Răspunsul la această întrebare este dat de formula Bayes. Schema de reevaluare a ipotezelor Echivalează părțile drepte ale acestor formule deci probabilitatea posterioară a ipotezei H k este Tabelul 1.3 - Reevaluarea ipotezelor H 1 - piesa primita de la primul furnizor H 2 - piesa primita de la un al doilea furnizor H 3 - parte primită de la un terț furnizor Exemplul #3. Există trei urne identice; prima urnă conține două bile albe și una neagră; în al doilea, trei albi și unul negru; în al treilea - două bile albe și două negre. Pentru experiment, o urna este aleasa la intamplare si se scoate o bila din ea. Găsiți probabilitatea ca această minge să fie albă. Exemplul #4. Există 19 puști în piramidă, 3 dintre ele cu vizor optic. Trăgătorul, trăgând dintr-o pușcă cu vizor optic, poate lovi ținta cu o probabilitate de 0,81, iar trăgând dintr-o pușcă fără vizor optic, cu o probabilitate de 0,46. Găsiți probabilitatea ca trăgătorul să lovească ținta trăgând dintr-o pușcă aleasă aleatoriu. Exemplul numărul 5. Dintr-o urna care contine 2 bile albe si 3 negre, se extrag doua bile la intamplare si se adauga 1 bile alba in urna. Găsiți probabilitatea ca o minge extrasă aleatoriu să fie albă. Exemplul numărul 6. Două focuri sunt trase în țintă. Probabilitatea de a lovi cu prima lovitură este de 0,2, cu a doua - 0,6. Probabilitatea de a distruge ținta cu o lovitură este de 0,3, cu două - 0,9. Găsiți probabilitatea ca ținta să fie distrusă.
Se știe că calitatea pieselor furnizate este diferită, iar la produsele primului furnizor, procentul de defecte este de 4%, al doilea - 5%, al treilea - 2%. Determinați probabilitatea ca o piesă selectată la întâmplare dintre toate primite să fie defectă.
P(H1) = 0,5; P(H2) = 0,2; P(H3) = 0,3
P(A|H1) = 0,04; P(A|H2) = 0,05; P(A|H3) = 0,02
P(A) = P(H1) P(A|H1) + P(H2) P(A|H2) + P(H3) P(A|H3) = 0,5 0,04 + 0,2 0,05 + 0,3 0,02=0,036
Probabilitatea ca o piesă aleasă la întâmplare să fie defectă este de 0,036.
Am început analiza probabilităților doar cu valori preliminare, a priori, ale probabilităților de evenimente. Apoi a fost făcut un experiment (a fost aleasă o parte) și am ajuns Informații suplimentare despre evenimentul de interes. Cu aceste noi informații, putem rafina valorile probabilităților anterioare. Noile valori ale probabilităților acelorași evenimente vor fi deja probabilități a posteriori (post-experimentale) ale ipotezelor (Fig. 1.5).
Fie ca evenimentul A să se realizeze numai împreună cu una dintre ipotezele H 1 , H 2 , …, H n (grup complet de evenimente incompatibile). Am notat a priori probabilități ale ipotezelor P(H i) probabilități condiționate ale evenimentului A - P(A|H i), i = 1, 2,…, n. Dacă experimentul a fost deja efectuat și ca urmare a acestuia a avut loc evenimentul A, atunci probabilitățile a posteriori ale ipotezelor vor fi probabilitățile condiționate P(H i |A), i = 1, 2,…, n. În notarea exemplului anterior, P(H 1 |A) este probabilitatea ca piesa selectată, care s-a dovedit a fi defectă, să fi fost primită de la primul furnizor.
Suntem interesați de probabilitatea evenimentului H k |A Considerăm apariția în comun a evenimentelor H k și A, adică evenimentul AH k . Probabilitatea sa poate fi găsită în două moduri, folosind formulele de înmulțire (1.5) și (1.6):
P(AHk) = P(Hk)P(A|Hk);
P(AH k) = P(A)P(H k |A).
P(H k) P(A|H k) = P(A) P(H k |A),![]()
Numitorul este probabilitatea totală a evenimentului A. Înlocuind în loc de P(A) valoarea acestuia conform formulei probabilității totale (1.11), obținem:  (1.12)
(1.12)
Formula (1.12) se numește Formula Bayes
și este folosit pentru a reevalua probabilitățile ipotezelor.
În condițiile exemplului anterior, găsim probabilitatea ca piesa defectă să fi fost primită de la primul furnizor. Să rezumam într-un tabel probabilitățile a priori ale ipotezelor P(H i) cunoscute nouă prin condiția, probabilitățile condiționate P(A|H i) probabilitățile comune calculate în procesul de rezolvare a P(AH i) = P(H i) P(A|H i) și calculată prin formula (1.12) probabilități a posteriori P(H k |A), i, k = 1, 2,…, n (Tabelul 1.3).
Luați în considerare ultimul rând al acestui tabel. A doua coloană conține suma probabilităților de evenimente incompatibile H 1 , H 2 , H 3 care formează un grup complet: Ipoteze Bună Probabilități
P(H i) anterior Condițional P(A|H i) Articulație P(AH i) A posteriori P(H i |A)
1
2
3
4
5
0.5
0.04
0.02
0.2
0.05
0.01
0.3
0.02
0.006
Sumă 1.0
-
0.036
1
P(Ω) = P(H1 + H2 + H3) = P(H1) + P(H2) + P(H3) = 0,5 + 0,2 + 0,3 = 1
În a patra coloană, valoarea din fiecare rând (probabilități comune) se obține prin regula înmulțirii probabilităților prin înmulțirea valorilor corespunzătoare din coloana a doua și a treia, iar în ultimul rând 0,036 este probabilitatea totală a evenimentului A (prin formula probabilității totale).
În coloana 5, probabilitățile posterioare ale ipotezelor sunt calculate folosind formula Bayes (1.12):
Probabilitățile posterioare P(H 2 |A) și P(H 3 |A) se calculează în mod similar, numărătorul fracției fiind probabilitățile comune înregistrate în rândurile corespunzătoare ale coloanei 4, iar numitorul fiind probabilitatea totală a evenimentul A înregistrat în ultimul rând al coloanei 4.
Suma probabilităților ipotezelor după experiment este egală cu 1 și este scrisă în ultima linie a coloanei a cincea.
Deci, probabilitatea ca piesa defectă să fie primită de la primul furnizor este de 0,555. Probabilitatea post-experimentală este mai mare decât cea a priori (datorită volumului mare de ofertă). Probabilitatea post-experimentală ca piesa defectă să fie primită de la al doilea furnizor este de 0,278 și este, de asemenea, mai mare decât cea pre-experimentală (datorită un numar mare căsătorie). Probabilitatea post-experimental ca o piesă defectă să fi fost obținută de la un al treilea furnizor este de 0,167.
Soluţie. Să luăm în considerare trei ipoteze: H 1 - se alege prima urna, H 2 - se alege a doua urna, H 3 - se alege a treia urna și evenimentul A - se scoate mingea albă.
Întrucât ipotezele sunt la fel de probabile după condiția problemei, atunci
Probabilitățile condiționate ale evenimentului A în aceste ipoteze sunt, respectiv, egale:
Conform formulei probabilității totale 
Soluţie. Aici primul test este o alegere aleatorie a puștii, al doilea este tragerea la țintă. Luați în considerare următoarele evenimente: A - trăgătorul va lovi ținta; H 1 - trăgătorul va lua o pușcă cu vizor optic; H 2 - trăgătorul va lua o pușcă fără vizor optic. Folosim formula probabilității totale. Avem
Având în vedere că puștile sunt selectate pe rând și folosind formula clasică de probabilitate, obținem: P(H 1) = 3/19, P(H 2) = 16/19.
Probabilitățile condiționate sunt date în enunțul problemei: P(A|H 1) = 0;81 și P(A|H 2) = 0;46. Prin urmare,
Soluţie. Evenimentul „se extrage o bilă albă” va fi notat cu A. Evenimentul H 1 - două bile albe sunt extrase la întâmplare; H 2 - două bile negre au fost extrase la întâmplare; H 3 - au fost extrase o bilă albă și una neagră. Apoi probabilitățile ipotezelor propuse
Probabilitățile condiționate din aceste ipoteze sunt, respectiv, egale: P(A|H 1) = 1/4 - probabilitatea de a extrage o minge albă dacă urna conține acest moment o bile albă și trei bile negre, P(A|H 2) = 3/4 - probabilitatea de a extrage o bilă albă dacă în prezent există trei bile albe și una neagră în urnă, P(A|H 3) = 2/ 4 = 1/2 - probabilitatea de a extrage o bilă albă dacă în urna sunt două bile albe și două negre în acest moment. Conform formulei probabilității totale 
Soluţie. Fie evenimentul A scopul este distrus. Pentru a face acest lucru, este suficient să loviți cu o lovitură din două sau să loviți ținta la rând cu două lovituri fără ratare. Să propunem ipoteze: H 1 - ambele lovituri lovesc ținta. Atunci P(H1) = 0,2 0,6 = 0;12. H 2 - fie prima dată, fie a doua oară s-a făcut o ratare. Apoi P (H 2) \u003d 0,2 0,4 + 0,8 0,6 \u003d 0,56. Ipoteza H 3 - ambele lovituri au fost ratate - nu este luată în considerare, deoarece probabilitatea distrugerii țintei este zero. Atunci probabilitățile condiționate sunt, respectiv, egale: probabilitatea de distrugere a țintei în condițiile ambelor lovituri reușite este P(A|H 1) = 0,9, iar probabilitatea de distrugere a țintei în condițiile unei singure lovituri reușite este P( A|H2) = 0,3. Atunci probabilitatea de a distruge ținta conform formulei probabilității totale este egală cu.