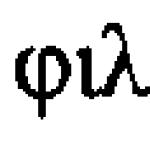Definiţie: Punctul x0 se numește punct de maxim local (sau minim) al unei funcții dacă într-o vecinătate a punctului x0 funcția ia cea mai mare (sau cea mai mică) valoare, adică. pentru toți x din vreo vecinătate a punctului x0 condiția f(x) f(x0) (sau f(x) f(x0)) este îndeplinită.

Punctele maxime sau minime locale sunt combinate nume comun- punctele extremului local al funcției.

Rețineți că la punctele extreme locale funcția atinge maximul sau cea mai mică valoare doar într-o zonă locală. Pot exista cazuri când în funcție de valoarea уmaxуmin.

Un semn necesar al existenței unui extremum local al unei funcții

Teorema . Dacă functie continua y = f(x) are un extremum local în punctul x0, atunci în acest punct derivata întâi este fie zero, fie nu există, adică. un extremum local apare în punctele critice de primul fel.

În punctele extreme locale, fie tangenta este paralelă cu axa 0x, fie există două tangente (vezi figura). Rețineți că punctele critice sunt o condiție necesară, dar nu suficientă pentru un extremum local. Un extremum local apare numai în punctele critice de primul fel, dar nu în toate punctele critice apare un extremum local.

De exemplu: o parabolă cubică y = x3 are un punct critic x0 = 0, la care derivata y/(0)=0, dar punctul critic x0=0 nu este un punct extremum și există un punct de inflexiune la el (vezi mai jos).

Un semn suficient al existenței unui extremum local al unei funcții

Teorema . Dacă, când argumentul trece printr-un punct critic de primul fel de la stânga la dreapta, prima derivată y / (x)

schimbă semnul din „+” în „-”, apoi funcția continuă y(x) în acest punct critic are un maxim local;

schimbă semnul din „-” în „+”, atunci funcția continuă y(x) are un minim local în acest punct critic

nu își schimbă semnul, atunci în acest punct critic nu există un extremum local, aici există un punct de inflexiune.

Pentru un maxim local, regiunea funcției crescătoare (y/0) este înlocuită cu regiunea funcției descrescătoare (y/0). Pentru un minim local, regiunea funcției descrescătoare (y/0) este înlocuită cu regiunea funcției crescătoare (y/0).

Exemplu: Examinați funcția y = x3 + 9x2 + 15x - 9 pentru monotonitate, extremum și construiți un grafic al funcției.

Să găsim punctele critice de primul fel definind derivata (y/) și echivalând-o cu zero: y/ = 3x2 + 18x + 15 = 3(x2 + 6x + 5) = 0

Să decidem trinom pătratic folosind un discriminant:

x2 + 6x + 5 = 0 (a=1, b=6, c=5) D=, x1k = -5, x2k = -1.

2) Împărțim axa numerelor în 3 regiuni cu puncte critice și determinăm semnele derivatei (y/) în ele. Folosind aceste semne vom găsi zone de monotonitate (crescând și descrescătoare) ale funcțiilor, iar prin schimbarea semnelor vom determina punctele de extremum local (maxim și minim).

Prezentăm rezultatele cercetării sub forma unui tabel, din care se pot trage următoarele concluzii:

• 1. Pe intervalul y /(-10) 0 funcția crește monoton (semnul derivatei y a fost estimat folosind punctul de control x = -10 luat în acest interval);
• 2. Pe intervalul (-5 ; -1) y /(-2) 0 funcția scade monoton (semnul derivatei y a fost estimat folosind punctul de control x = -2, luat în acest interval);
• 3. Pe intervalul y /(0) 0, funcția crește monoton (semnul derivatei y a fost estimat folosind punctul de control x = 0, luat în acest interval);
• 4. La trecerea prin punctul critic x1k = -5, derivata își schimbă semnul din „+” în „-”, prin urmare acest punct este un punct maxim local
• (ymax(-5) = (-5)3+9(-5)2 +15(-5)-9=-125 + 225 - 75 - 9 =16);
• 5. La trecerea prin punctul critic x2k = -1, derivata își schimbă semnul din „-” în „+”, prin urmare acest punct este un punct minim local
• (ymin(-1) = -1 + 9 - 15 - 9 = - 16).

x -5 (-5; -1) -1

3) Vom construi un grafic pe baza rezultatelor studiului folosind calcule suplimentare ale valorilor funcției la punctele de control:

construiți un sistem de coordonate dreptunghiular Oxy;

Arătăm prin coordonate punctele de maxim (-5; 16) și minim (-1;-16);

pentru a clarifica graficul, calculăm valoarea funcției la punctele de control, selectându-le în stânga și în dreapta punctelor maxime și minime și în interiorul intervalului mediu, de exemplu: y(-6)=(-6)3 + 9(-6)2+15(-6)-9=9; y(-3)=(-3)3+9(-3)2+15(-3)-9=0;

y(0)= -9 (-6;9); (-3;0) și (0;-9) - puncte de control calculate pe care le trasăm pentru a construi graficul;

Prezentăm graficul sub forma unei curbe convexe în sus în punctul maxim și convexe în jos în punctul minim și trecând prin punctele de control calculate.

>> Extrema

Extremul funcției

Definiţia extremum

Funcţie y = f(x) se numește crescând (în scădere) într-un anumit interval, dacă pentru x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f (x 2)).

Dacă funcția diferențiabilă y = f (x) crește (descrește) pe un interval, atunci derivata sa pe acest interval f " (x)> 0

(f"(x)< 0).

Punct x O numit punct maxim local (minim) funcţia f (x) dacă există o vecinătate a punctului x o, pentru toate punctele pentru care inegalitatea f (x) este adevărată≤ f (x o ) (f (x)≥ f (x o )).

Se numesc punctele maxime și minime puncte extremum, iar valorile funcției în aceste puncte sunt ale acesteia extreme.

Puncte extreme

Condiții necesare pentru un extremum . Dacă punctul x O este punctul extremum al funcției f (x), atunci fie f " (x o ) = 0 sau f(x o ) nu există. Se numesc astfel de puncte critic, iar funcția în sine este definită în punctul critic. Extremele unei funcții ar trebui căutate printre punctele sale critice.

Prima condiție suficientă. Lasă x O - punct critic. Dacă f" (x ) la trecerea printr-un punct x O schimbă semnul plus în minus, apoi la punctul x o functia are un maxim, altfel are un minim. Dacă, la trecerea prin punctul critic, derivata nu își schimbă semnul, atunci în punctul x O nu exista extrema.

A doua condiție suficientă. Fie funcția f(x) să aibă
f" (x ) în vecinătatea punctului x O iar derivata a doua la punctul însuși x o. Dacă f"(x o) = 0, >0 ( <0), то точка x o este punctul minim (maxim) local al funcției f (x). Dacă =0, atunci trebuie fie să utilizați prima condiție suficientă, fie să implicați altele mai mari.

Pe un segment, funcția y = f (x) își poate atinge valoarea minimă sau maximă fie în punctele critice, fie la capetele segmentului.

Exemplul 3.22.

Soluţie. Deoarece f " (

Probleme de găsire a extremului unei funcții

Exemplul 3.23. o

Soluţie. xŞi y y
0 ≤ x≤
> 0 și când x >a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение funcții kv. unitati).

Exemplul 3.24. p ≈

Soluţie. p p
S"
R = 2, H = 16/4 = 4.

Exemplul 3.22.Aflați extremele funcției f (x) = 2x 3 - 15x 2 + 36x - 14.

Soluţie. Deoarece f " (x ) = 6x 2 - 30x +36 = 6(x ​​​​-2)(x - 3), atunci punctele critice ale funcției x 1 = 2 și x 2 = 3. Extrema poate fi doar în aceste puncte. Deoarece la trecerea prin punctul x 1 = 2 derivata își schimbă semnul din plus în minus, atunci în acest punct funcția are un maxim. La trecerea prin punctul x 2 = 3, derivata își schimbă semnul din minus în plus, deci în punctul x 2 = 3 funcția are un minim. După ce au calculat valorile funcției la puncte
x 1 = 2 și x 2 = 3, găsim extremele funcției: maxim f (2) = 14 și minim f (3) = 13.

Exemplul 3.23.Este necesar să construiți o zonă dreptunghiulară lângă zidul de piatră, astfel încât să fie împrejmuită pe trei laturi cu plasă de sârmă, iar a patra latură să fie adiacentă peretelui. Pentru asta există o metri liniari de plasă. La ce raport de aspect va avea site-ul cea mai mare suprafață?

Soluţie.Să notăm părțile laterale ale platformei prin xŞi y. Aria sitului este S = xy. Lasă y- aceasta este lungimea laturii adiacente peretelui. Atunci, prin condiție, egalitatea 2x + y = a trebuie îndeplinită. Prin urmare y = a - 2x și S = x (a - 2x), unde
0 ≤ x≤ a /2 (lungimea și lățimea zonei nu pot fi negative). S " = a - 4x, a - 4x = 0 la x = a/4, de unde
y = a - 2 × a/4 =a/2. Deoarece x = a /4 este singurul punct critic să verificăm dacă semnul derivatei se modifică la trecerea prin acest punct. La x a /4 S "> 0 și când x >a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение funcții S(a/4) = a/4(a - a/2) = a 2 /8 (kv. unitati). Deoarece S este continuu și valorile sale la capete S(0) și S(a/2) sunt egale cu zero, atunci valoarea găsită va fi cea mai mare valoare funcții. Astfel, raportul de aspect cel mai favorabil al site-ului în condițiile date ale problemei este y = 2x.

Exemplul 3.24.Este necesară fabricarea unui rezervor cilindric închis cu o capacitate de V=16 p ≈ 50 m 3 . Care ar trebui să fie dimensiunile rezervorului (raza R și înălțimea H) pentru ca la fabricarea acestuia să se folosească cea mai mică cantitate de material?

Soluţie.Pătrat suprafata intreaga cilindrul este egal cu S = 2 p R(R+H). Cunoaștem volumul cilindrului V = p R 2 Н Þ Н = V/ p R 2 =16 p / p R2 = 16/R2. Deci S(R) = 2 p (R2+16/R). Găsim derivata acestei funcții:
S"(R) = 2 p (2R-16/R2) = 4 p (R-8/R2). S" (R) = 0 la R3 = 8, prin urmare,
R = 2, H = 16/4 = 4.

Pentru o funcție f(x) a mai multor variabile, punctul x este un vector, f'(x) este un vector de prime derivate (gradient) ale funcției f(x), f ′ ′(x) este o matrice simetrică de a doua derivate parțiale (matrice Hessian - Hessian) funcții f(x).
Pentru functia multora variabile de condiție optimitățile sunt formulate după cum urmează.
O condiție necesară pentru optimitatea locală. Fie f(x) derivabilă în punctul x * R n . Dacă x * este un punct extremum local, atunci f’(x *) = 0.
Ca și înainte, punctele care sunt soluții ale unui sistem de ecuații sunt numite staționare. Natura punctului staționar x * este asociată cu semnul definit al matricei hessiene f′ ′(x).
Semnul matricei A depinde de semnele formei pătratice Q(α)=< α A, α >pentru toate α∈R n nenule.
Aici și mai departe prin denotă produsul scalar al vectorilor x și y. Prin definiție,

O matrice A este pozitivă (nenegativă) definită dacă Q(α)>0 (Q(α)≥0) pentru toate α∈R n nenule; negativ (nepozitiv) definit dacă Q(α)<0 (Q(α)≤0) при всех ненулевых α∈R n ; неопределенной, если Q(α)>0 pentru unele α∈R n și Q(α) diferite de zero<0 для остальных ненулевых α∈R n .
Condiție suficientă pentru optimitatea locală. Fie f(x) diferentiabil de doua ori in punctul x * R n, si f’(x *)=0, i.e. x * − punct staționar. Atunci, dacă matricea f′′(x *) este pozitivă (negativă) definită, atunci x * este un punct minim (maxim) local; dacă matricea f′′(x *) este nedefinită, atunci x * este un punct de șa.
Dacă matricea f′′(x *) este definită nenegativ (nepozitiv), atunci pentru a determina natura punctului staționar x * este nevoie de studiul derivatelor de ordin superior.
Pentru a verifica semnul unei matrice, de regulă, se folosește criteriul Sylvester. Conform acestui criteriu, o matrice simetrică A este definită pozitivă dacă și numai dacă toate unghiularele sale minore sunt pozitive. În acest caz, minorul unghiular al matricei A este determinantul unei matrice construite din elemente ale matricei A situate la intersecția rândurilor și coloanelor cu aceleași (și primele) numere. Pentru a verifica matricea simetrică A pentru definiție negativă, trebuie să verificați matricea (−A) pentru definiție pozitivă.
Deci, algoritmul pentru determinarea punctelor extreme locale ale unei funcții de mai multe variabile este următorul.
1. Aflați f′(x).
2. Sistemul este în curs de rezolvare

Ca rezultat, punctele staționare x i sunt calculate.
3. Aflați f′′(x), setați i=1.
4. Aflați f′′(x i)
5. Se calculează minorele unghiulare ale matricei f′′(x i). Dacă nu toate minorele unghiulare sunt diferite de zero, atunci determinarea naturii punctului staționar x i necesită studiul derivatelor de ordin superior. În acest caz, trecerea la pasul 8 este efectuată.
În caz contrar, treceți la pasul 6.
6. Se analizează semnele minorelor unghiulare f′′(x i). Dacă f′′(x i) este definit pozitiv, atunci x i este un punct minim local. În acest caz, trecerea la pasul 8 este efectuată.
În caz contrar, treceți la pasul 7.
7. Se calculează minorele unghiulare ale matricei -f′′(x i) și se analizează semnele acestora.
Dacă -f′′(x i) − este definit pozitiv, atunci f′′(x i) este definit negativ și x i este un punct maxim local.
În caz contrar, f′′(x i) este nedefinit și x i este un punct de șa.
8. Se verifică condiţia de determinare a naturii tuturor punctelor staţionare i=N.
Dacă este îndeplinită, atunci calculele sunt finalizate.
Dacă condiția nu este îndeplinită, atunci se presupune i=i+1 și se realizează trecerea la pasul 4.

Exemplul nr. 1. Determinați punctele extremelor locale ale funcției f(x) = x 1 3 – 2x 1 x 2 + x 2 2 – 3x 1 – 2x 2









Deoarece toate minorele unghiulare sunt diferite de zero, caracterul lui x 2 este determinat folosind f′′(x).
Deoarece matricea f′′(x 2) este definită pozitiv, x 2 este un punct minim local.
Răspuns: funcția f(x) = x 1 3 – 2x 1 x 2 + x 2 2 – 3x 1 – 2x 2 are un minim local în punctul x = (5/3; 8/3).

Se spune că funcția are în punctul intern
regiune D maxim local(minim), dacă există o astfel de vecinătate a punctului
, pentru fiecare punct
care deține inegalitatea

Dacă o funcţie are într-un punct
maxim local sau minim local, atunci spunem că are în acest punct extremul local(sau doar o extremă).

Teorema (condiție necesară pentru existența unui extremum). Dacă funcţia diferenţiabilă atinge un extrem în punct
, apoi fiecare derivată parțială de ordinul întâi a funcției în acest moment devine zero.

Sunt numite punctele în care toate derivatele parțiale de ordinul întâi dispar punctele staţionare ale funcţiei
. Coordonatele acestor puncte pot fi găsite prin rezolvarea sistemului de

.

ecuații

Condiția necesară pentru existența unui extremum în cazul unei funcții diferențiabile poate fi formulată pe scurt după cum urmează: Există cazuri când în puncte individuale unele derivate parțiale au valori infinite sau nu există (în timp ce restul sunt egale cu zero). Se numesc astfel de puncte punctele critice ale funcției.

Aceste puncte ar trebui, de asemenea, considerate „suspecte” pentru un extremum, la fel ca și cele staționare. În cazul unei funcţii a două variabile conditie necesara extremum, și anume egalitatea la zero a derivatelor parțiale (diferențiale) la punctul extremum, are o interpretare geometrică:
plan tangent la suprafata
.

la punctul extremum trebuie să fie paralel cu planul

20. Condiții suficiente pentru existența unui extremum
Îndeplinirea condiției necesare pentru existența unui extremum la un moment dat nu garantează deloc prezența unui extremum acolo. Ca exemplu, putem lua funcția diferențiabilă peste tot
.
Atât derivatele sale parțiale, cât și funcția în sine dispar la punct
.

Cu toate acestea, în orice vecinătate din acest punct există ambele pozitive (mari
definit, continuu si are derivate partiale continue pana la ordinul doi inclusiv in vecinatatea unui punct
, care este punctul staționar al funcției
, adică îndeplinește condițiile

,
.

Să introducem următoarea notație:

Teorema (condiţii suficiente pentru existenţa unui extremum). Lasă funcția
satisface conditiile de mai sus si anume: este diferentiabila intr-o vecinatate a unui punct stationar
și este de două ori diferențiabilă în punctul însuși
.

Atunci dacă
În cazul în care
apoi functia
la punct

ajunge maxim local
la

Şi maxim local
.

minim local
În general, pentru funcție
condiție suficientă pentru existența la punctminim(local maxim ) este(pozitiv negativ

) certitudinea celui de-al doilea diferential.

Teorema . Cu alte cuvinte, următoarea afirmație este adevărată.
Dacă la punct

pentru functie
pentru orice nu este egal cu zero în același timp minim, atunci în acest moment funcția are (asemănător cu maxim
).

, DacăExemplul 18.

Găsiți punctele extreme locale ale unei funcții Soluţie

. Să găsim derivatele parțiale ale funcției și să le echivalăm cu zero:

Rezolvând acest sistem, găsim două puncte extreme posibile:

Să găsim derivatele parțiale de ordinul doi pentru această funcție:
La primul punct staționar, așadar, și
Prin urmare, în acest moment sunt necesare cercetări suplimentare. Valoarea funcției
în acest moment este zero:

Următorul,

la

Următorul,

O
Prin urmare, în orice vecinătate a punctului
funcţie
ia valori la fel de mari
, și mai mici
Prin urmare, în orice vecinătate a punctului
, și, prin urmare, la punct

, prin definiție, nu are extremum local.



La al doilea punct staționar
deci, deci, din moment ce
apoi la punct

funcția are un maxim local. maxim local$E \subset \mathbb(R)^(n)$. Se spune că $f$ are

în punctul $x_(0) \în E$, dacă există o vecinătate $U$ a punctului $x_(0)$ astfel încât pentru toți $x \în U$ inegalitatea $f\left(x\right) ) \leqslant f este satisfăcută \left(x_(0)\right)$. Maximul local este numit strict< f\left(x_{0}\right)$.

, dacă vecinătatea $U$ poate fi aleasă astfel încât pentru toți $x \în U$ diferit de $x_(0)$ să existe $f\left(x\right)
Definiţie Fie $f$ o funcție reală pe mulțimea deschisă $E \subset \mathbb(R)^(n)$. Se spune că $f$ are minim local

în punctul $x_(0) \în E$, dacă există o vecinătate $U$ a punctului $x_(0)$ astfel încât inegalitatea $f\left(x\right) \geqslant f să fie valabilă pentru toți $ x \în U$ \left(x_(0)\right)$.

Extremul local combină conceptele de minim local și maxim local.

Teoremă (condiție necesară pentru extremul unei funcții diferențiabile)
Fie $f$ o funcție reală pe mulțimea deschisă $E \subset \mathbb(R)^(n)$. Dacă în punctul $x_(0) \în E$ funcția $f$ are o extremă locală în acest punct, atunci $$\text(d)f\left(x_(0)\right)=0.$$ Diferența egală cu zero este echivalentă cu faptul că toate sunt egale cu zero, adică. $$\displaystyle\frac(\partial f)(\partial x_(i))\left(x_(0)\right)=0.$$

În cazul unidimensional acesta este – . Să notăm $\phi \left(t\right) = f \left(x_(0)+th\right)$, unde $h$ este un vector arbitrar. Funcția $\phi$ este definită pentru valori de $t$ care sunt suficient de mici în valoare absolută. În plus, în ceea ce privește , este diferențiabilă și $(\phi)’ \left(t\right) = \text(d)f \left(x_(0)+th\right)h$.
Fie ca $f$ să aibă un maxim local în punctul x $0$. Aceasta înseamnă că funcția $\phi$ la $t = 0$ are un maxim local și, după teorema lui Fermat, $(\phi)’ \left(0\right)=0$.
Deci, am obținut că $df \left(x_(0)\right) = 0$, adică. funcția $f$ în punctul $x_(0)$ este egală cu zero pe orice vector $h$.

, dacă vecinătatea $U$ poate fi aleasă astfel încât pentru toți $x \în U$ diferit de $x_(0)$ să existe $f\left(x\right)
Puncte în care diferența este zero, adică cele în care toate derivatele parțiale sunt egale cu zero se numesc staționari. Puncte critice funcțiile $f$ sunt acele puncte în care $f$ nu este diferențiabilă sau este egală cu zero. Dacă punctul este staționar, atunci nu rezultă din aceasta că funcția are un extremum în acest punct.

Exemplul 1.
Fie $f \left(x,y\right)=x^(3)+y^(3)$. Apoi $\displaystyle\frac(\partial f)(\partial x) = 3 \cdot x^(2)$,$\displaystyle\frac(\partial f)(\partial y) = 3 \cdot y^(2 )$, deci $\left(0,0\right)$ este un punct staționar, dar funcția nu are nicio extremă în acest punct. Într-adevăr, $f \left(0,0\right) = 0$, dar este ușor de observat că în orice vecinătate a punctului $\left(0,0\right)$ funcția ia atât valori pozitive, cât și negative.

Exemplul 2.
Funcția $f \left(x,y\right) = x^(2) − y^(2)$ are un punct staționar la origine, dar este clar că nu există un extremum în acest punct.

Teoremă (condiție suficientă pentru extremum).
Fie funcția $f$ să fie de două ori diferențiabilă continuu pe mulțimea deschisă $E \subset \mathbb(R)^(n)$. Fie $x_(0) \in E$ un punct staționar și $$\displaystyle Q_(x_(0)) \left(h\right) \equiv \sum_(i=1)^n \sum_(j=1 ) ^n \frac(\partial^(2) f)(\partial x_(i) \partial x_(j)) \left(x_(0)\right)h^(i)h^(j).$ $ Atunci

1. dacă $Q_(x_(0))$ – , atunci funcția $f$ în punctul $x_(0)$ are un extremum local și anume un minim dacă forma este definită pozitivă și un maxim dacă forma este definit negativ;
2. dacă forma pătratică $Q_(x_(0))$ este nedefinită, atunci funcția $f$ în punctul $x_(0)$ nu are extremă.

Să folosim expansiunea conform formulei lui Taylor (12.7 p. 292). Considerând că derivatele parțiale de ordinul întâi în punctul $x_(0)$ sunt egale cu zero, obținem $$\displaystyle f \left(x_(0)+h\right)−f \left(x_(0)\ dreapta) = \ frac(1)(2) \sum_(i=1)^n \sum_(j=1)^n \frac(\partial^(2) f)(\partial x_(i) \partial x_ (j)) \left(x_(0)+\theta h\right)h^(i)h^(j),$$ unde $0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0$ și $\epsilon \left(h\right) \rightarrow 0$ pentru $h \rightarrow 0$, atunci partea dreaptă va fi pozitivă pentru orice vector $h$ de lungime suficient de mică.
Deci, am ajuns la concluzia că într-o anumită vecinătate a punctului $x_(0)$ inegalitatea $f \left(x\right) >f \left(x_(0)\right)$ este valabilă dacă numai $ x \neq x_ (0)$ (punem $x=x_(0)+h$\dreapta). Aceasta înseamnă că în punctul $x_(0)$ funcția are un minim local strict și astfel se demonstrează prima parte a teoremei noastre.
Să presupunem acum că $Q_(x_(0))$ – formă nedefinită. Apoi există vectori $h_(1)$, $h_(2)$ astfel încât $Q_(x_(0)) \left(h_(1)\right)=\lambda_(1)>0$, $Q_ ( x_(0)) \left(h_(2)\right)= \lambda_(2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>0 USD. Apoi obținem $$f \left(x_(0)+th_(1)\right)−f \left(x_(0)\right) = \frac(1)(2) \left[ t^(2) \ lambda_(1) + t^(2) |h_(1)|^(2) \epsilon \left(th_(1)\right) \right] = \frac(1)(2) t^(2) \ left[ \lambda_(1) + |h_(1)|^(2) \epsilon \left(th_(1)\right) \right].$$ Pentru $t>0$ suficient de mic, mâna dreaptă partea este pozitivă. Aceasta înseamnă că în orice vecinătate a punctului $x_(0)$ funcția $f$ ia valori $f \left(x\right)$ mai mari decât $f \left(x_(0)\right)$.
În mod similar, constatăm că în orice vecinătate a punctului $x_(0)$ funcția $f$ ia valori mai mici decât $f \left(x_(0)\right)$. Aceasta, împreună cu cea precedentă, înseamnă că în punctul $x_(0)$ funcția $f$ nu are un extremum.

Să considerăm un caz special al acestei teoreme pentru funcția $f \left(x,y\right)$ a două variabile, definite într-o vecinătate a punctului $\left(x_(0),y_(0)\right )$ și având derivate parțiale continue de ordinul întâi și al doilea. Să presupunem că $\left(x_(0),y_(0)\right)$ este un punct staționar și indică $$\displaystyle a_(11)= \frac(\partial^(2) f)(\partial x ^ (2)) \left(x_(0) ,y_(0)\right), a_(12)=\frac(\partial^(2) f)(\partial x \partial y) \left(x_( 0) ), y_(0)\right), a_(22)=\frac(\partial^(2) f)(\partial y^(2)) \left(x_(0), y_(0)\right ) .$$ Atunci teorema anterioară ia următoarea formă.

Teorema
Fie $\Delta=a_(11) \cdot a_(22) − a_(12)^2$. Apoi:

1. dacă $\Delta>0$, atunci funcția $f$ are un extremum local în punctul $\left(x_(0),y_(0)\right)$ și anume un minim dacă $a_(11)> 0$ și maxim dacă $a_(11)<0$;
2. dacă $\Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.

Exemple de rezolvare a problemelor

Algoritm pentru găsirea extremului unei funcții a mai multor variabile:

1. Găsirea punctelor staționare;
2. Găsiți diferența de ordinul 2 în toate punctele staționare
3. Folosind condiția suficientă pentru extremul unei funcții de mai multe variabile, considerăm diferența de ordinul 2 la fiecare punct staționar

1. Investigați funcția pentru extremul $f \left(x,y\right) = x^(3) + 8 \cdot y^(3) + 18 \cdot x — 30 \cdot y$.
   Soluţie

   Să găsim derivatele parțiale de ordinul I: $$\displaystyle \frac(\partial f)(\partial x)=3 \cdot x^(2) - 6 \cdot y;$$ $$\displaystyle \frac(\partial f)(\partial y)=24 \cdot y^(2) - 6 \cdot x.$$ Să compunem și să rezolvăm sistemul: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x) = 0\\\frac(\partial f)(\partial y)= 0\end(cases) \Rightarrow \begin(cases)3 \cdot x^(2) - 6 \cdot y= 0\\24 \cdot y^(2) — 6 \cdot x = 0\end(cases) \Rightarrow \begin(cases)x^(2) — 2 \cdot y= 0\\4 \cdot y^(2) — x = 0 \end(cases)$$ Din a 2-a ecuație exprimăm $x=4 \cdot y^(2)$ - înlocuiți-l în prima ecuație: $$\displaystyle \left(4 \cdot y^(2) \right )^(2)-2 \cdot y=0$$ $$16 \cdot y^(4) — 2 \cdot y = 0$$ $$8 \cdot y^(4) — y = 0$$ $ $y \left(8 \cdot y^(3) -1\right)=0$$ Ca rezultat, se obțin 2 puncte staționare:
   1) $y=0 \Rightarrow x = 0, M_(1) = \left(0, 0\right)$;
   2) $\displaystyle 8 \cdot y^(3) -1=0 \Rightarrow y^(3)=\frac(1)(8) \Rightarrow y = \frac(1)(2) \Rightarrow x=1 , M_(2) = \left(\frac(1)(2), 1\right)$
   Să verificăm dacă este îndeplinită condiția suficientă pentru un extremum:
   $$\displaystyle \frac(\partial^(2) f)(\partial x^(2))=6 \cdot x; \frac(\partial^(2) f)(\partial x \partial y)=-6; \frac(\partial^(2) f)(\partial y^(2))=48 \cdot y$$
   1) Pentru punctul $M_(1)= \left(0,0\right)$:
   $$\displaystyle A_(1)=\frac(\partial^(2) f)(\partial x^(2)) \left(0,0\right)=0; B_(1)=\frac(\partial^(2) f)(\partial x \partial y) \left(0,0\right)=-6; C_(1)=\frac(\partial^(2) f)(\partial y^(2)) \left(0,0\right)=0;$$
   $A_(1) \cdot B_(1) — C_(1)^(2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
   2) Pentru punctul $M_(2)$:
   $$\displaystyle A_(2)=\frac(\partial^(2) f)(\partial x^(2)) \left(1,\frac(1)(2)\right)=6; B_(2)=\frac(\partial^(2) f)(\partial x \partial y) \left(1,\frac(1)(2)\right)=-6; C_(2)=\frac(\partial^(2) f)(\partial y^(2)) \left(1,\frac(1)(2)\right)=24;$$
   $A_(2) \cdot B_(2) — C_(2)^(2) = 108>0$, ceea ce înseamnă că în punctul $M_(2)$ există un extremum, iar din moment ce $A_(2)> 0$, atunci acesta este minimul.
   Răspuns: Punctul $\displaystyle M_(2)\left(1,\frac(1)(2)\right)$ este punctul minim al funcției $f$.
   

2. Investigați funcția pentru extremul $f=y^(2) + 2 \cdot x \cdot y - 4 \cdot x - 2 \cdot y - 3$.
   Soluţie

   Să găsim puncte staționare: $$\displaystyle \frac(\partial f)(\partial x)=2 \cdot y - 4;$$ $$\displaystyle \frac(\partial f)(\partial y)=2 \ cdot y + 2 \cdot x — 2.$$
   Să compunem și să rezolvăm sistemul: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x)= 0\\\frac(\partial f)(\partial y)= 0\end(cases) ) \ Săgeată la dreapta \begin(cases)2 \cdot y - 4= 0\\2 \cdot y + 2 \cdot x - 2 = 0\end(cases) \Rightarrow \begin(cases) y = 2\\y + x = 1\end(cases) \Rightarrow x = -1$$
   $M_(0) \left(-1, 2\right)$ este un punct staționar.
   Să verificăm dacă este îndeplinită condiția suficientă pentru extremum: $$\displaystyle A=\frac(\partial^(2) f)(\partial x^(2)) \left(-1,2\right)=0 ; B=\frac(\partial^(2) f)(\partial x \partial y) \left(-1,2\right)=2; C=\frac(\partial^(2) f)(\partial y^(2)) \left(-1,2\right)=2;$$
   $A \cdot B — C^(2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
   Răspuns: nu există extreme.
   

Limita de timp: 0

Navigare (numai numere de job)

0 din 4 sarcini finalizate

Informaţii

Faceți acest test pentru a vă testa cunoștințele despre subiectul pe care tocmai l-ați citit: Extreme locale ale funcțiilor multiplelor variabile.

Ai susținut deja testul înainte. Nu o poți porni din nou.

Test de încărcare...

Trebuie să vă autentificați sau să vă înregistrați pentru a începe testul.

Trebuie să finalizați următoarele teste pentru a începe acesta:

Rezultate

Răspunsuri corecte: 0 din 4

Ora ta:

Timpul a trecut

Ai obținut 0 din 0 puncte (0)

Rezultatul dvs. a fost înregistrat pe clasament

1. Cu răspuns
2. Cu un semn de vizualizare

Sarcina 1 din 4

1 .

Numar de puncte: 1

Investigați funcția $f$ pentru extreme: $f=e^(x+y)(x^(2)-2 \cdot y^(2))$

Corect


Greşit


1. Sarcina 2 din 4

   2 .

   Numar de puncte: 1

   Funcția $f = 4 + \sqrt((x^(2)+y^(2))^(2))$ are un extremum