Koncepcja równoległoboku
Definicja 1
Równoległobok to czworokąt, w którym przeciwne strony są do siebie równoległe (ryc. 1).
Obrazek 1.
Równoległobok ma dwie główne właściwości. Rozważmy je bez dowodu.
Właściwość 1: Przeciwległe boki i kąty równoległoboku są odpowiednio równe.
Właściwość 2: Przekątne narysowane w równoległoboku są podzielone na pół przez punkt przecięcia.
Znaki równoległoboku
Rozważmy trzy cechy równoległoboku i przedstawmy je w formie twierdzeń.
Twierdzenie 1
Jeśli dwa boki czworokąta są sobie równe i równoległe, to czworokąt ten będzie równoległobokiem.
Dowód.
Dajmy sobie czworokąt $ABCD$. W którym $AB||CD$ i $AB=CD$ Narysujmy w nim przekątną $AC$ (rys. 2).

Rysunek 2.
Rozważmy linie równoległe $AB$ i $CD$ oraz ich sieczną $AC$. Następnie
\[\kąt CAB=\kąt DCA\]
jak skrzyżowane rogi.
Zgodnie z kryterium $I$ równości trójkątów,
ponieważ $AC$ jest ich wspólną stroną, a $AB=CD$ według warunku. Oznacza
\[\kąt DAC=\kąt ACB\]
Rozważmy proste $AD$ i $CB$ oraz ich sieczną $AC$; z ostatniej równości kątów leżących otrzymujemy $AD||CB$.) Zatem z definicji $1$ ten czworokąt jest równoległobokiem.
Twierdzenie zostało udowodnione.
Twierdzenie 2
Jeśli przeciwne strony czworokąta są sobie równe, to jest to równoległobok.
Dowód.
Dajmy sobie czworokąt $ABCD$. Gdzie $AD=BC$ i $AB=CD$. Narysujmy w nim przekątną $AC$ (rys. 3).

Rysunek 3.
Ponieważ $AD=BC$, $AB=CD$ i $AC$ są wspólnym bokem, to zgodnie z kryterium $III$ równości trójkątów
\[\trójkąt DAC=\trójkąt ACB\]
\[\kąt DAC=\kąt ACB\]
Rozważmy proste $AD$ i $CB$ oraz ich sieczną $AC$; z ostatniej równości kątów leżących otrzymamy $AD||CB$. Dlatego z definicji $1$ ten czworokąt jest równoległobokiem.
\[\kąt DCA=\kąt CAB\]
Rozważmy proste $AB$ i $CD$ oraz ich sieczne $AC$; z ostatniej równości kątów leżących otrzymamy $AB||CD$. Dlatego zgodnie z definicją 1 ten czworokąt jest równoległobokiem.
Twierdzenie zostało udowodnione.
Twierdzenie 3
Jeśli przekątne narysowane w czworokącie zostaną podzielone na dwie równe części przez punkt przecięcia, to ten czworokąt jest równoległobokiem.
Dowód.
Dajmy sobie czworokąt $ABCD$. Narysujmy w nim przekątne $AC$ i $BD$. Niech przecinają się w punkcie $O$ (ryc. 4).
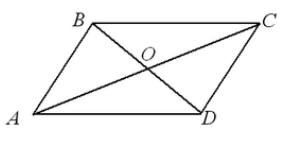
Rysunek 4.
Ponieważ zgodnie z warunkiem $BO=OD,\ AO=OC$ i kąty $\angle COB=\angle DOA$ są pionowe, to zgodnie z kryterium $I$ równości trójkątów,
\[\trójkąt BOC=\trójkąt AOD\]
\[\kąt DBC=\kąt BDA\]
Rozważmy proste $BC$ i $AD$ oraz ich sieczną $BD$; z ostatniej równości kątów leżących otrzymamy $BC||AD$. Również $BC=AD$. Zatem zgodnie z twierdzeniem $1$ ten czworokąt jest równoległobokiem.
Równoległobok to czworokąt, którego przeciwne boki są równoległe, tj. leżą na liniach równoległych
Właściwości równoległoboku:  Twierdzenie 22.
Przeciwległe boki równoległoboku są równe.
Twierdzenie 22.
Przeciwległe boki równoległoboku są równe.
Dowód. W równoległoboku ABCD rysujemy przekątną AC. Trójkąty ACD i ACB są równe, ponieważ mają wspólny bok AC i dwie pary równe kąty. sąsiadujące z nim: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (jako kąty poprzeczne z równoległymi liniami AD i BC). Oznacza to, że AB = CD i BC = AD, jako odpowiadające boki równych trójkątów itp. Z równości tych trójkątów wynika również, że odpowiednie kąty trójkątów są równe:
Twierdzenie 23.
Przeciwległe kąty równoległoboku są równe: ∠ A=∠ C i ∠ B=∠ D.
Równość pierwszej pary wynika z równości trójkątów ABD i CBD, a drugiej - ABC i ACD.
Twierdzenie 24.
Sąsiednie kąty równoległoboku, tj. kąty przylegające do jednej strony sumują się do 180 stopni.
Dzieje się tak, ponieważ są to kąty wewnętrzne jednostronne.
Twierdzenie 25.
Przekątne równoległoboku przecinają się w punkcie przecięcia.
Dowód. Rozważmy trójkąty BOC i AOD. Zgodnie z pierwszą własnością AD=BC ∠ OAD=∠ OCB i ∠ ODA=∠ OBC leżące poprzecznie dla prostych równoległych AD i BC. Dlatego trójkąty BOC i AOD są równe pod kątem bocznym i przyległym. Oznacza to BO=OD i AO=OS, podobnie jak odpowiadające im boki równych trójkątów itp.
Znaki równoległoboku
Twierdzenie 26.
Jeżeli przeciwne strony czworokąta są równe parami, to jest to równoległobok.
Dowód. Niech czworokąt ABCD ma odpowiednio równe boki AD i BC, AB i CD (rys. 2). Narysujmy przekątną AC. Trójkąty ABC i ACD są równe z trzech stron. Wtedy kąty BAC i DCA są sobie równe, zatem AB jest równoległy do CD. Równoległość boków BC i AD wynika z równości kątów CAD i ACB.
Twierdzenie 27.
Jeśli przeciwne kąty czworokąta są równe parami, to jest to równoległobok.
Niech ∠ A=∠ C i ∠ B=∠ D. Ponieważ ∠ A+∠ B+∠ C+∠ D=360 o, następnie ∠ A+∠ B=180 o i boki AD i BC są równoległe (w oparciu o równoległość linii prostych). Udowodnimy również równoległość boków AB i CD i dochodzimy do wniosku, że ABCD jest z definicji równoległobokiem.
Twierdzenie 28.
Jeżeli sąsiednie narożniki czworoboku, tj. Kąty sąsiadujące z jednym bokiem sumują się do 180 stopni, wtedy jest to równoległobok.
Jeśli wewnętrzne kąty jednostronne sumują się do 180 stopni, wówczas linie proste są równoległe. Zatem AB jest równoległe do CD, a BC jest równoległe do AD. Z definicji czworokąt jest równoległobokiem.
Twierdzenie 29.
Jeżeli przekątne czworokąta przecinają się w punkcie przecięcia, to czworokąt jest równoległobokiem.
Dowód. Jeśli AO = OC, BO = OD, to trójkąty AOD i BOC są równe, ponieważ mają równe (pionowe) kąty w wierzchołku O, zawarte pomiędzy parami równych boków. Z równości trójkątów wnioskujemy, że AD i BC są równe. Boki AB i CD są również równe, a czworokąt okazuje się równoległobokiem zgodnie z kryterium 1.
Twierdzenie 30.
Jeśli czworokąt ma parę równych, równoległych boków, to jest równoległobokiem.
Niech boki AB i CD czworokąta ABCD będą równoległe i równe. Narysujmy przekątne AC i BD. Z równoległości tych prostych wynika, że kąty poprzeczne ABO = CDO i BAO = OCD są równe. Trójkąty ABO i CDO mają równe kąty boczne i przyległe. Zatem AO=OS, VO=ОD, tj. Przekątne dzieli się na pół w punkcie przecięcia i czworokąt okazuje się równoległobokiem zgodnie z kryterium 4.
W geometrii rozważa się szczególne przypadki równoległoboków.
Podczas rozwiązywania problemów na ten temat, z wyjątkiem podstawowe właściwości równoległobok i odpowiednie formuły, możesz zapamiętać i zastosować następujące zasady:
- Dwusieczna kąta wewnętrznego równoległoboku odcina od niego trójkąt równoramienny
- Dwusieczne kątów wewnętrznych przylegających do jednego z boków równoległoboku są wzajemnie prostopadłe
- Dwusieczne wychodzące z przeciwległych narożników wewnętrznych równoległoboku są do siebie równoległe lub leżą na tej samej linii prostej
- Suma kwadratów przekątnych równoległoboku jest równa sumie kwadratów jego boków
- Pole równoległoboku jest równe połowie iloczynu przekątnych i sinusa kąta między nimi
Rozważmy problemy, w których te właściwości są wykorzystywane.
Zadanie 1.
Dwusieczna kąta C równoległoboku ABCD przecina bok AD w punkcie M i kontynuację boku AB poza punktem A w punkcie E. Znajdź obwód równoległoboku, jeśli AE = 4, DM = 3.
Rozwiązanie.
1. Trójkąt CMD jest równoramienny. (Właściwość 1). Dlatego CD = MD = 3 cm.
2. Trójkąt EAM jest równoramienny.
Dlatego AE = AM = 4 cm.
3. AD = AM + MD = 7 cm.
4. Obwód ABCD = 20 cm.
Odpowiedź. 20 cm.
Zadanie 2.
W wypukłym czworoboku ABCD narysowano przekątne. Wiadomo, że pola trójkątów ABD, ACD, BCD są równe. Udowodnić, że ten czworokąt jest równoległobokiem.

Rozwiązanie.
1. Niech BE będzie wysokością trójkąta ABD, CF będzie wysokością trójkąta ACD. Ponieważ zgodnie z warunkami zadania pola trójkątów są równe i mają wspólną podstawę AD, to wysokości tych trójkątów są równe. BE = CF.
2. BE, CF są prostopadłe do AD. Punkty B i C leżą po tej samej stronie względem prostej AD. BE = CF. Dlatego prosta BC || OGŁOSZENIE. (*)
3. Niech AL będzie wysokością trójkąta ACD, BK wysokością trójkąta BCD. Ponieważ zgodnie z warunkami zadania pola trójkątów są równe i mają wspólną podstawę CD, to wysokości tych trójkątów są równe. AL = BK.
4. AL i BK są prostopadłe do CD. Punkty B i A leżą po tej samej stronie względem prostej CD. AL = BK. Dlatego prosta AB || PŁYTA CD (**)
5. Z warunków (*), (**) wynika, że ABCD jest równoległobokiem.
Odpowiedź. Udowodniony. ABCD jest równoległobokiem.
Zadanie 3.
Na bokach BC i CD równoległoboku ABCD zaznaczono odpowiednio punkty M i H, tak aby odcinki BM i HD przecinały się w punkcie O;<ВМD = 95 о,
 Rozwiązanie.
Rozwiązanie.
1. W trójkącie DOM<МОD = 25 о (Он смежный с <ВОD = 155 о); <ОМD = 95 о. Тогда <ОDМ = 60 о.
2. W trójkącie prostokątnym DHC Następnie<НСD = 30 о. СD: НD = 2: 1 Ale CD = AB. Wtedy AB: HD = 2: 1. 3. <С = 30 о, 4. <А = <С = 30 о, <В = Odpowiedź: AB: HD = 2: 1,<А = <С = 30 о, <В = Zadanie 4. Jedna z przekątnych równoległoboku o długości 4√6 tworzy z podstawą kąt 60°, a druga przekątna tworzy z tą samą podstawą kąt 45°. Znajdź drugą przekątną. Rozwiązanie.
1. AO = 2√6. 2. Stosujemy twierdzenie sinusoidalne do trójkąta AOD. AO/grzech D = OD/grzech A. 2√6/sin 45 o = OD/sin 60 o. ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6. Odpowiedź: 12.
Zadanie 5. W przypadku równoległoboku o bokach 5√2 i 7√2 mniejszy kąt między przekątnymi jest równy mniejszemu kątowi równoległoboku. Znajdź sumę długości przekątnych. Rozwiązanie.
Niech d 1, d 2 będą przekątnymi równoległoboku, a kąt między przekątnymi a mniejszym kątem równoległoboku jest równy φ. 1. Policzmy dwa różne S ABCD = AB AD grzech A = 5√2 7√2 grzech f, S ABCD = 1/2 AC ─ D sin AOB = 1/2 d 1 d 2 grzech f. Otrzymujemy równość 5√2 · 7√2 · sin f = 1/2d 1 d 2 sin f lub 2 · 5√2 · 7√2 = re 1 re 2 ; 2. Korzystając z zależności między bokami i przekątnymi równoległoboku, zapisujemy równość (AB 2 + AD 2) 2 = AC 2 + BD 2. ((5√2) 2 + (7√2) 2) 2 = re 1 2 + re 2 2. re 1 2 + re 2 2 = 296. 3. Stwórzmy system: (d 1 2 + d 2 2 = 296, Pomnóżmy drugie równanie układu przez 2 i dodajmy je do pierwszego. Otrzymujemy (d 1 + d 2) 2 = 576. Stąd Id 1 + d 2 I = 24. Ponieważ d 1, d 2 są długościami przekątnych równoległoboku, wówczas d 1 + d 2 = 24. Odpowiedź: 24.
Zadanie 6. Boki równoległoboku mają długość 4 i 6. Kąt ostry między przekątnymi wynosi 45 stopni. Znajdź obszar równoległoboku. Rozwiązanie.
1. Z trójkąta AOB, korzystając z twierdzenia o cosinusie, zapisujemy związek między bokiem równoległoboku a przekątnymi. AB 2 = AO 2 + VO 2 2 · AO · VO · cos AOB. 4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1/2) · (d 2 /2)cos 45 o; re 1 2 /4 + re 2 2 /4 – 2 · (d 1/2) · (d 2 /2)√2/2 = 16. re 1 2 + re 2 2 – re 1 · re 2 √2 = 64. 2. Podobnie zapisujemy relację dla trójkąta AOD. Weźmy to pod uwagę<АОD = 135 о и cos 135 о = -cos 45 о = -√2/2. Otrzymujemy równanie d 1 2 + d 2 2 + d 1 · d 2 √2 = 144. 3. Mamy system Odejmując pierwsze od drugiego równania, otrzymujemy 2d 1 · d 2 √2 = 80 lub re 1 re 2 = 80/(2√2) = 20√2 4. S ABCD = 1/2 AC ÂD sin AOB = 1/2 d 1 d 2 sin α = 1/2 20√2 √2/2 = 10. Notatka: W tym i poprzednim problemie nie ma potrzeby całkowitego rozwiązywania układu, zakładając, że w tym zadaniu potrzebny będzie iloczyn przekątnych do obliczenia pola. Odpowiedź: 10. Zadanie 7. Pole równoległoboku wynosi 96, a jego boki to 8 i 15. Znajdź kwadrat mniejszej przekątnej. Rozwiązanie.
1. S ABCD = AB · AD · grzech · AD. Dokonajmy podstawienia we wzorze. Otrzymujemy 96 = 8 · 15 · sin ВAD. Stąd grzech ─AD = 4/5. 2. Znajdźmy cos VAD. grzech 2 VAD + cos 2 VAD = 1. (4 / 5) 2 + cos 2 VAD = 1. cos 2 VAD = 9 / 25. Zgodnie z warunkami zadania znajdujemy długość mniejszej przekątnej. Przekątna ВD będzie mniejsza, jeśli kąt ВАD jest ostry. Wtedy cos VAD = 3/5. 3. Z trójkąta ABD, korzystając z twierdzenia cosinus, znajdujemy kwadrat przekątnej BD. ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВAD. ─ 2 = 8 2 + 15 2 – 2 8 15 3 / 5 = 145. Odpowiedź: 145.
Nadal masz pytania? Nie wiesz jak rozwiązać zadanie z geometrii? stronie internetowej, przy kopiowaniu materiału w całości lub w części wymagany jest link do źródła. Równoległobok to czworokąt, którego przeciwne boki są równoległe parami. Poniższy rysunek przedstawia równoległobok ABCD. Ma bok AB równoległy do boku CD i bok BC równoległy do boku AD. Jak można się domyślić, równoległobok jest wypukłym czworokątem. Rozważmy podstawowe właściwości równoległoboku. 1. W równoległoboku przeciwne kąty i przeciwne boki są równe. Udowodnijmy tę własność - rozważmy równoległobok przedstawiony na poniższym rysunku. Przekątna BD dzieli ją na dwa równe trójkąty: ABD i CBD. Są one równe wzdłuż boku BD i dwóch sąsiadujących z nim kątów, ponieważ kąty leżą poprzecznie na siecznej BD równoległych linii odpowiednio BC i AD oraz AB i CD. Dlatego AB = CD i 2. Przekątne równoległoboku są podzielone na pół w punkcie przecięcia. Niech punkt O będzie punktem przecięcia przekątnych AC i BD równoległoboku ABCD. Wtedy trójkąt AOB i trójkąt COD są sobie równe, wzdłuż boku i dwóch sąsiednich kątów. (AB = CD, ponieważ są to przeciwne strony równoległoboku. A kąt1 = kąt2 i kąt3 = kąt4 są jak kąty poprzeczne, gdy proste AB i CD przecinają się odpowiednio z siecznymi AC i BD.) Z tego wynika, że AO = OC i OB = OD, co należało udowodnić. Wszystkie główne właściwości zilustrowano na poniższych trzech rysunkach. „Ważne odkrycie naukowe dostarcza rozwiązania poważnego problemu, ale w rozwiązaniu każdego problemu jest ziarno odkrycia”. Równoległobok ma przeciwne strony, które są równe. Dowód. Niech ABCD będzie danym równoległobokiem. I niech jego przekątne przecinają się w punkcie O. W równoległoboku przeciwległe kąty są równe. Dowód. Przekątne równoległoboku przecinają się i są podzielone na pół w punkcie przecięcia. Dowód. Niech ABCD będzie danym równoległobokiem. Narysujmy przekątną AC. Zaznaczmy na nim środkowe O. Kontynuując odcinek DO, odłożymy na bok odcinek OB 1 równy DO. W podręcznikach dla zwykłych szkół (na przykład w Pogorełowie) udowodniono to w ten sposób: przekątne dzielą równoległobok na 4 trójkąty. Rozważmy jedną parę i dowiedzmy się - są równe: ich podstawy są przeciwległymi bokami, odpowiednie kąty przylegające do niej są równe, jak kąty pionowe z liniami równoległymi. Oznacza to, że odcinki przekątnych są równe parami. Wszystko. Czy to wszystko? Zabawne jest to, że tę część znacznie trudniej jest udowodnić. Nawiasem mówiąc, wynika to z bardziej ogólnego wyniku: w każdym wypukłym czworokącie przekątne będą się przecinać, ale w każdym niewypukłym czworokącie nie. O równości trójkątów wzdłuż boku i dwóch sąsiednich kątów (drugi znak równości trójkątów) i innych. Thales znalazł ważne praktyczne zastosowanie twierdzenia o równości dwóch trójkątów wzdłuż boku i dwóch sąsiednich kątów. W porcie Miletu zbudowano dalmierz, który miał określać odległość do statku na morzu. Składał się z trzech wbijanych kołków A, B i C (AB = BC) oraz zaznaczonej linii prostej SC, prostopadłej do CA. Kiedy statek pojawił się na linii prostej SK, znaleźliśmy punkt D taki, że punkty D, .B i E leżały na tej samej linii prostej. Jak widać na rysunku, odległość CD na ziemi jest pożądaną odległością od statku. Pracowaliśmy nad lekcją Kuzniecow A.V. Poturnak S.A. Jewgienij Pietrow Można zadać pytanie dotyczące współczesnej edukacji, wyrazić pomysł lub rozwiązać palący problem pod adresem Forum edukacyjne, gdzie rada edukacyjna świeżych myśli i działań spotyka się na arenie międzynarodowej. Stworzywszy blog, Nie tylko podniesiesz swój status kompetentnego nauczyciela, ale także wniesiesz znaczący wkład w rozwój szkoły przyszłości. Gildia Liderów Oświaty otwiera drzwi dla najwyższej klasy specjalistów i zaprasza ich do współpracy przy tworzeniu najlepszych szkół na świecie.
(
(Ponieważ w trójkącie prostokątnym noga leżąca naprzeciw kąta 30° jest równa połowie przeciwprostokątnej).
 sposoby na jego obszar.
sposoby na jego obszar.
(d 1 + re 2 = 140.
(d 1 2 + re 2 2 – re 1 · re 2 √2 = 64,
(d 1 2 + re 2 2 + re 1 · re 2 √2 = 144.
Aby uzyskać pomoc korepetytora zarejestruj się.
Pierwsza lekcja jest bezpłatna!
Właściwości równoległoboku

BC = AD. A z równości kątów 1, 2, 3 i 4 wynika, że kąt A = kąt1 + kąt3 = kąt2 + kąt4 = kąt C.
Temat lekcji
Cele Lekcji
Cele Lekcji
Plan lekcji
Wstęp

Własność przeciwległych boków równoległoboku
Ponieważ Δ AOB = Δ COD według pierwszego kryterium równości trójkątów (∠ AOB = ∠ COD, jako pionowe, AO=OC, DO=OB, według własności przekątnych równoległoboku), to AB=CD. W ten sam sposób z równości trójkątów BOC i DOA wynika, że BC = DA. Twierdzenie zostało udowodnione. Własność kątów przeciwnych równoległoboku
Niech ABCD będzie danym równoległobokiem. I niech jego przekątne przecinają się w punkcie O.
Z tego, co zostało udowodnione w twierdzeniu o własnościach przeciwległych boków równoległoboku Δ ABC = Δ CDA z trzech stron (AB=CD, BC=DA z tego, co zostało udowodnione, AC – ogólnie). Z równości trójkątów wynika, że ∠ ABC = ∠ CDA.
Udowodniono także, że ∠ DAB = ∠ BCD, co wynika z ∠ ABD = ∠ CDB. Twierdzenie zostało udowodnione.Własność przekątnych równoległoboku
Zgodnie z poprzednim twierdzeniem AB 1 CD jest równoległobokiem. Dlatego linia AB 1 jest równoległa do DC. Ale przez punkt A można poprowadzić tylko jedną linię równoległą do DC. Oznacza to, że prosta AB 1 pokrywa się z prostą AB.
Udowodniono również, że BC 1 pokrywa się z BC. Oznacza to, że punkt C pokrywa się z C 1. równoległobok ABCD pokrywa się z równoległobokiem AB 1 CD. W rezultacie przekątne równoległoboku przecinają się i są podzielone na pół w punkcie przecięcia. Twierdzenie zostało udowodnione.
Udowodniono powyżej, że punkt przecięcia przecina przekątne na pół - jeśli istnieje. Powyższe rozumowanie w żaden sposób nie dowodzi jego istnienia. Oznacza to, że część twierdzenia „przekątne równoległoboku przecinają się” pozostaje niepotwierdzona.
pytania
Lista wykorzystanych źródeł


