Lygiagretainio samprata
1 apibrėžimas
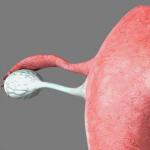
Lygiagretainis yra keturkampis, kurio priešingos kraštinės yra lygiagrečios viena kitai (1 pav.).
1 paveikslas.
Lygiagretainis turi dvi pagrindines savybes. Panagrinėkime juos be įrodymų.
1 nuosavybė: Lygiagretainio priešingos kraštinės ir kampai yra atitinkamai lygūs vienas kitam.
2 nuosavybė: Lygiagretainiu nubrėžtos įstrižainės dalinamos pusiau pagal jų susikirtimo tašką.
Lygiagretainės savybės
Apsvarstykite tris lygiagretainio požymius ir pateikite juos teoremų pavidalu.
1 teorema
Jei dvi keturkampio kraštinės yra lygios viena kitai ir lygiagrečios, tai šis keturkampis bus lygiagretainis.
Įrodymas.
Pateikiame keturkampį $ABCD$. Kuriame $AB||CD$ ir $AB=CD$ Nubrėžkime įstrižainę $AC$ (2 pav.).

2 pav.
Apsvarstykite lygiagrečias tieses $AB$ ir $CD$ bei jų sekantą $AC$. Tada
\[\angle CAB=\angle DCA\]
kaip skersiniai kampai.
Pagal $I$ trikampių lygybės kriterijų,
nes $AC$ yra jų bendra pusė, o $AB=CD$ pagal prielaidą. Reiškia
\[\angle DAC=\angle ACB\]
Apsvarstykite tieses $AD$ ir $CB$ bei jų sekantą $AC$; pagal paskutinę kryžminių kampų lygybę gauname, kad $AD||CB$.) Todėl pagal $1$ apibrėžimą šis keturkampis yra lygiagretainis.
Teorema įrodyta.
2 teorema
Jei keturkampio priešingos kraštinės yra lygios, tai yra lygiagretainis.
Įrodymas.
Pateikiame keturkampį $ABCD$. Kuriame $AD=BC$ ir $AB=CD$. Nubrėžkime jame įstrižainę $AC$ (3 pav.).

3 pav
Kadangi $AD=BC$, $AB=CD$ ir $AC$ yra bendra pusė, tai $III$ trikampio lygybės testas,
\[\triangle DAC=\triangle ACB\]
\[\angle DAC=\angle ACB\]
Apsvarstykite eilutes $AD$ ir $CB$ bei jų sekantą $AC$, pagal paskutinę kryžminių kampų lygybę gauname $AD||CB$. Todėl pagal $1$ apibrėžimą šis keturkampis yra lygiagretainis.
\[\angle DCA=\angle CAB\]
Apsvarstykite eilutes $AB$ ir $CD$ bei jų sekantą $AC$, pagal paskutinę kryžminių kampų lygybę gauname $AB||CD$. Todėl pagal 1 apibrėžimą šis keturkampis yra lygiagretainis.
Teorema įrodyta.
3 teorema
Jei keturkampyje nubrėžtos įstrižainės pagal jų susikirtimo tašką padalinamos į dvi lygias dalis, tai šis keturkampis yra lygiagretainis.
Įrodymas.
Pateikiame keturkampį $ABCD$. Nubrėžkime jame įstrižaines $AC$ ir $BD$. Tegul jie susikerta taške $O$ (4 pav.).
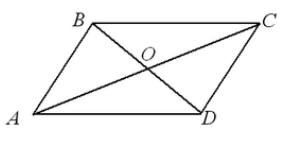
4 pav
Kadangi pagal sąlygą $BO=OD,\AO=OC$ ir kampai $\angle COB=\kampas DOA$ yra vertikalūs, tai $I$ trikampio lygybės testu,
\[\triangle BOC=\triangle AOD\]
\[\angle DBC=\angle BDA\]
Apsvarstykite eilutes $BC$ ir $AD$ bei jų sekantą $BD$, pagal paskutinę kryžminių kampų lygybę gauname $BC||AD$. Taip pat $BC=AD$. Todėl pagal teoremą $1$ šis keturkampis yra lygiagretainis.
Lygiagretainis yra keturkampis, kurio priešingos kraštinės yra lygiagrečios, t.y. gulėti ant lygiagrečių linijų
Lygiagretainės savybės:  22 teorema.
Lygiagretainio priešingos kraštinės yra lygios.
22 teorema.
Lygiagretainio priešingos kraštinės yra lygios.
Įrodymas. Lygiagretainio ABCD nubrėžkite įstrižainę AC. Trikampiai ACD ir ACB sutampa kaip turintys bendrą kraštinę AC ir dvi poras vienodi kampai. greta jo: ∠ CAB=∠ ACD, ∠ ASV=∠ DAC (kaip kryžminiai kampai su lygiagrečiomis tiesėmis AD ir BC). Vadinasi, AB = CD ir BC = AD kaip atitinkamos lygių trikampių kraštinės ir kt. Šių trikampių lygybė taip pat reiškia atitinkamų trikampių kampų lygybę:
23 teorema.
Lygiagretainio priešingi kampai yra: ∠ A=∠ C ir ∠ B=∠ D.
Pirmosios poros lygybė gaunama iš trikampių ABD ir CBD lygybės, o antrosios - ABC ir ACD.
24 teorema.
Gretimi lygiagretainio kampai, t.y. kampai, esantys šalia vienos pusės, sudaro 180 laipsnių.
Taip yra todėl, kad jie yra vidiniai vienpusiai kampai.
25 teorema.
Lygiagretainio įstrižainės viena kitą dalija jų susikirtimo taške.
Įrodymas. Apsvarstykite trikampius BOC ir AOD. Pagal pirmąją savybę AD=BC ∠ ОАD=∠ OSV ir ∠ ОDA=∠ ОВС kaip skersai lygiagrečių linijų AD ir BC. Todėl trikampių BOC ir AOD kraštinės ir kampai, esantys šalia jo, yra vienodi. Vadinasi, BO=OD ir AO=OC, kaip atitinkamos lygių trikampių kraštinės ir kt.
Lygiagretainės savybės
26 teorema.
Jei keturkampio priešingos kraštinės yra lygios poromis, tai yra lygiagretainis.
Įrodymas. Tegu keturkampio ABCD kraštinės AD ir BC, AB ir CD atitinkamai lygios (2 pav.). Nubrėžkime įstrižainę AC. Trikampis ABC ir ACD turi tris lygias kraštines. Tada kampai BAC ir DCA yra lygūs, todėl AB lygiagreti CD. Kraštinių BC ir AD lygiagretumas išplaukia iš kampų CAD ir DIA lygybės.
27 teorema.
Jei keturkampio priešingi kampai poromis lygūs, tai lygiagretainis.
Tegu ∠ A=∠ C ir ∠ B=∠ D. ∠ A+∠ B+∠ C+∠ D=360 o, tada ∠ A+∠ B=180 o ir kraštinės AD ir BC lygiagrečios (lygiagrečių tiesių pagrindu). Taip pat įrodome kraštinių AB ir CD lygiagretumą ir darome išvadą, kad ABCD pagal apibrėžimą yra lygiagretainis.
28 teorema.
Jei gretimi keturkampio kampai, t.y. kampai, esantys greta vienos pusės, sumuojasi iki 180 laipsnių, tada tai yra lygiagretainis.
Jei vidiniai vienpusiai kampai sudaro 180 laipsnių, tada linijos yra lygiagrečios. Tai reiškia, kad AB yra CD pora, o BC yra AD pora. Keturkampis pagal apibrėžimą pasirodo esąs lygiagretainis.
29 teorema.
Jei keturkampio įstrižainės susikirtimo taške dalijamos per pusę, tai keturkampis yra lygiagretainis.
Įrodymas. Jei AO=OC, BO=OD, tai trikampiai AOD ir BOC yra lygūs, kaip turintys lygius kampus (vertikalius) viršūnėje O, uždarytuose tarp lygių kraštinių porų. Iš trikampių lygybės darome išvadą, kad AD ir BC yra lygūs. AB ir CD kraštinės taip pat yra lygios, o keturkampis pagal 1 požymį pasirodo lygiagretainiu.
30 teorema.
Jei keturkampis turi porą lygiagrečių lygiagrečių kraštinių, tai jis yra lygiagretainis.
Tegul kraštinės AB ir CD yra lygiagrečios ir lygios keturkampyje ABCD. Nubrėžkite įstrižaines AC ir BD. Iš šių tiesių lygiagretumo išplaukia kryžminio gulėjimo kampų lygybė ABO=CDO ir BAO=OCD. Trikampiai ABO ir CDO yra lygūs šoniniuose ir gretimuose kampuose. Todėl AO=OC, BO=OD, t.y. susikirtimo taško įstrižainės dalijamos pusiau ir keturkampis pagal 4 požymį pasirodo lygiagretainiu.
Geometrijoje nagrinėjami ypatingi lygiagretainio atvejai.
Sprendžiant problemas šia tema, be pagrindinės savybės lygiagretainis ir atitinkamas formules, galite atsiminti ir taikyti:
- Lygiagretainio vidinio kampo bisektorius atkerta iš jo lygiašonį trikampį
- Vidinių kampų bisektoriai, esantys greta vienos iš lygiagretainio kraštinių, yra statmeni vienas kitam
- Bisektoriai, kylantys iš priešingų vidinių lygiagretainio kampų, lygiagrečiai vienas kitam arba yra vienoje tiesėje
- Lygiagretainio įstrižainių kvadratų suma lygi jo kraštinių kvadratų sumai
- Lygiagretainio plotas yra pusė įstrižainių sandaugos, padaugintos iš kampo tarp jų sinuso.
Panagrinėkime užduotis, kurias sprendžiant naudojamos šios savybės.
1 užduotis.
Lygiagretainio ABCD kampo C bisektorius kerta kraštinę AD taške M ir kraštinės AB tęsinį už taško A taške E. Raskite lygiagretainio perimetrą, jei AE \u003d 4, DM \u003d 3.
Sprendimas.
1. Trikampis CMD lygiašonis. (1 nuosavybė). Todėl CD = MD = 3 cm.
2. Trikampis EAM yra lygiašonis.
Todėl AE = AM = 4 cm.
3. AD = AM + MD = 7 cm.
4. Perimetras ABCD = 20 cm.
Atsakymas. 20 cm
2 užduotis.
Išgaubtame keturkampyje ABCD brėžiamos įstrižainės. Yra žinoma, kad trikampių ABD, ACD, BCD plotai yra lygūs. Įrodykite, kad duotasis keturkampis yra lygiagretainis.

Sprendimas.
1. Tegu BE yra trikampio ABD aukštis, CF – trikampio ACD aukštis. Kadangi pagal uždavinio sąlygą trikampių plotai yra lygūs ir jie turi bendrą pagrindą AD, tai šių trikampių aukščiai yra vienodi. BE = CF.
2. BE, CF yra statmenos AD. Taškai B ir C yra toje pačioje AD linijos pusėje. BE = CF. Todėl linija BC || REKLAMA. (*)
3. Tegu AL yra trikampio ACD aukštis, BK – trikampio BCD aukštis. Kadangi pagal uždavinio sąlygą trikampių plotai yra lygūs ir jie turi bendrą pagrindą CD, tai šių trikampių aukščiai yra vienodi. AL = BK.
4. AL ir BK yra statmenos CD. Taškai B ir A yra toje pačioje tiesios linijos CD pusėje. AL = BK. Todėl eilutė AB || CD (**)
5. Sąlygos (*), (**) reiškia, kad ABCD yra lygiagretainis.
Atsakymas. Įrodyta. ABCD yra lygiagretainis.
3 užduotis.
Lygiagretainio ABCD kraštinėse BC ir CD atitinkamai pažymėti taškai M ir H, kad atkarpos BM ir HD susikirstų taške O;<ВМD = 95 о,
 Sprendimas.
Sprendimas.
1. Trikampyje DOM<МОD = 25 о (Он смежный с <ВОD = 155 о); <ОМD = 95 о. Тогда <ОDМ = 60 о.
2. Stačiame trikampyje DHC Tada<НСD = 30 о. СD: НD = 2: 1 Bet CD = AB. Tada AB: HD = 2:1. 3. <С = 30 о, 4. <А = <С = 30 о, <В = Atsakymas: AB: HD = 2:1,<А = <С = 30 о, <В = 4 užduotis. Viena iš 4√6 ilgio lygiagretainio įstrižainių sudaro 60° kampą su pagrindu, o antroji įstrižainė sudaro 45° kampą su tuo pačiu pagrindu. Raskite antrąją įstrižainę. Sprendimas.
1. AO = 2√6. 2. Taikykite sinuso teoremą trikampiui AOD. AO/sin D = OD/sin A. 2√6/sin 45 o = OD/sin 60 o. OD = (2√6sin 60 o) / sin 45 o = (2√6 √3/2) / (√2/2) = 2√18/√2 = 6. Atsakymas: 12.
5 užduotis. Lygiagretainio, kurio kraštinės yra 5√2 ir 7√2, mažesnis kampas tarp įstrižainių yra lygus mažesniam lygiagretainio kampui. Raskite įstrižainių ilgių sumą. Sprendimas.
Tegu lygiagretainio įstrižainės yra d 1, d 2, o kampas tarp įstrižainių ir mažesniojo lygiagretainio kampo lygus φ. 1. Suskaičiuokime du skirtingus S ABCD \u003d AB AD sin A \u003d 5√2 7√2 sin f, S ABCD \u003d 1/2 AC BD sin AOB \u003d 1/2 d 1 d 2 sin f. Gauname lygybę 5√2 7√2 sin f = 1/2d 1 d 2 sin f arba 2 5√2 7√2 = d 1 d 2; 2. Naudodami santykį tarp lygiagretainio kraštinių ir įstrižainių, užrašome lygybę (AB 2 + AD 2) 2 = AC 2 + BD 2. ((5√2) 2 + (7√2) 2) 2 = d 1 2 + d 2 2 . d 1 2 + d 2 2 = 296. 3. Sukurkime sistemą: (d 1 2 + d 2 2 = 296, Padauginkite antrąją sistemos lygtį iš 2 ir pridėkite prie pirmosios. Gauname (d 1 + d 2) 2 = 576. Taigi Id 1 + d 2 I = 24. Kadangi d 1, d 2 yra lygiagretainio įstrižainių ilgiai, tai d 1 + d 2 = 24. Atsakymas: 24.
6 užduotis. Lygiagretainio kraštinės yra 4 ir 6. Smailusis kampas tarp įstrižainių lygus 45 o. Raskite lygiagretainio plotą. Sprendimas.
1. Iš trikampio AOB, naudodamiesi kosinuso teorema, užrašome ryšį tarp lygiagretainio kraštinės ir įstrižainių. AB 2 \u003d AO 2 + VO 2 2 AO VO cos AOB. 4 2 \u003d (d 1 / 2) 2 + (d 2 / 2) 2 - 2 (d 1 / 2) (d 2 / 2) cos 45 o; d 1 2/4 + d 2 2/4 - 2 (d 1/2) (d 2/2)√2/2 = 16. d 1 2 + d 2 2 - d 1 d 2 √2 = 64. 2. Panašiai rašome santykį trikampiui AOD. Atsižvelgiame į tai<АОD = 135 о и cos 135 о = -cos 45 о = -√2/2. Gauname lygtį d 1 2 + d 2 2 + d 1 d 2 √2 = 144. 3. Mes turime sistemą Iš antrosios lygties atėmę pirmąjį, gauname 2d 1 d 2 √2 = 80 arba d 1 d 2 = 80/(2√2) = 20√2 4. S ABCD \u003d 1/2 AC BD sin AOB \u003d 1/2 d 1 d 2 sin α \u003d 1/2 20√2 √2/2 \u003d 10. Pastaba:Šiame ir ankstesniame uždavinyje nereikia visiškai spręsti sistemos, numatant, kad šiame uždavinyje plotui apskaičiuoti reikia įstrižainių sandaugos. Atsakymas: 10. 7 užduotis. Lygiagretainio plotas yra 96, o jo kraštinės yra 8 ir 15. Raskite mažesnės įstrižainės kvadratą. Sprendimas.
1. S ABCD \u003d AB AD sin VAD. Atlikime pakeitimą formulėje. Gauname 96 = 8 15 sin VAD. Taigi nuodėmė VAD = 4/5. 2. Rasti cos BAD. sin 2 VAD + cos 2 VAD = 1. (4/5) 2 + cos 2 BLOGAS = 1. cos 2 BLOGAS = 9/25. Pagal uždavinio sąlygą randame mažesnės įstrižainės ilgį. Įstrižainė BD bus mažesnė, jei kampas BAD smailus. Tada BLOGAS = 3/5. 3. Iš trikampio ABD, pasitelkę kosinuso teoremą, randame įstrižainės BD kvadratą. BD 2 \u003d AB 2 + AD 2 - 2 AB BD cos BAD. ВD 2 \u003d 8 2 + 15 2 - 2 8 15 3 / 5 \u003d 145. Atsakymas: 145.
Ar turite kokių nors klausimų? Nežinote, kaip išspręsti geometrijos problemą? svetainę, visiškai ar iš dalies nukopijavus medžiagą, būtina nuoroda į šaltinį. Lygiagretainis yra keturkampis, kurio priešingos kraštinės yra poromis lygiagrečios. Toliau pateiktame paveikslėlyje parodyta lygiagretainė ABCD. Jos kraštinė AB lygiagreti kraštinei CD ir kraštinė BC lygiagreti kraštinei AD. Kaip jau spėjote, lygiagretainis yra išgaubtas keturkampis. Apsvarstykite pagrindines lygiagretainio savybes. 1. Lygiagrečiame priešingi kampai ir priešingos kraštinės yra lygūs. Įrodykime šią savybę – apsvarstykite lygiagretainį, pavaizduotą kitame paveikslėlyje. Įstrižainė BD padalija ją į du vienodus trikampius: ABD ir CBD. Jie yra lygūs kraštinėje BD ir du gretimi kampai, nes kampai, esantys ties BD sekante, yra lygiagrečios tiesės BC ir AD bei AB ir CD atitinkamai. Todėl AB = CD ir 2. Lygiagretainio įstrižainės dalinamos per susikirtimo tašką. Tegul taškas O yra lygiagretainio ABCD įstrižainių AC ir BD susikirtimo taškas. Tada trikampis AOB ir trikampis COD yra lygūs vienas kitam, išilgai kraštinės ir dviejų gretimų kampų. (AB=CD, nes jos yra priešingos lygiagretainio kraštinės. O kampas1 = kampas2 ir kampas3 = kampas4 kaip kryžminiai kampai tiesių AB ir CD sankirtoje atitinkamai per sekantais AC ir BD.) Iš to išplaukia, kad AO = OC ir OB = OD, kurį ir reikėjo įrodyti. Visos pagrindinės savybės parodytos trijuose paveikslėliuose. „Didysis mokslinis atradimas yra pagrindinės problemos sprendimas, tačiau bet kurios problemos sprendimas yra atradimų grūdelis“. Lygiagretainio priešingos kraštinės yra lygios. Įrodymas. Tegu ABCD yra duotasis lygiagretainis. Ir tegul jos įstrižainės susikerta taške O. Lygiagretainis turi priešingus kampus. Įrodymas. Lygiagretainio įstrižainės susikerta, o susikirtimo taškas yra padalintas į pusę. Įrodymas. Tegu ABCD yra duotasis lygiagretainis. Nubrėžkime įstrižainę AC. Ant jo pažymime vidurinį O. Atkarpos DO tęsinyje atidėjame atkarpą OB 1, lygią DO. Paprastų mokyklų vadovėliuose (pavyzdžiui, Pogorelove) tai įrodoma taip: įstrižainės padalija lygiagretainį į 4 trikampius. Apsvarstykite vieną porą ir sužinokite - jos yra lygios: jų pagrindai yra priešingos pusės, atitinkami kampai, esantys greta jos, yra lygūs vertikaliems su lygiagrečiomis linijomis. Tai yra, įstrižainių atkarpos yra poromis lygios. Visi. Ar tai viskas? Juokinga, kad šią dalį daug sunkiau įrodyti. Beje, tai išplaukia iš bendresnio rezultato: bet kurio išgaubto keturkampio įstrižainės susikirs, bet kurio neišgaubto – ne. Apie trikampių lygybę išilgai kraštinės ir dviejų šalia jos esančių kampų (antrasis trikampių lygybės ženklas) ir kt. Teorema apie dviejų trikampių lygybę išilgai šono ir dviejų šalia jos esančių kampų Thales rado svarbų praktinį pritaikymą. Mileto uoste buvo pastatytas nuotolio ieškiklis, kuris nustato atstumą iki laivo jūroje. Jį sudarė trys varomi kaiščiai A, B ir C (AB = BC) ir pažymėta tiesi linija SK, statmena CA. Kai laivas pasirodė tiesėje SC, buvo rastas taškas D, kad taškai D, .B ir E būtų toje pačioje tiesėje. Kaip matyti iš brėžinio, atstumas CD ant žemės yra norimas atstumas iki laivo. Darbas prie pamokos Kuznecovas A.V. Poturnak S.A. Jevgenijus Petrovas Galite iškelti klausimą apie šiuolaikinį švietimą, išsakyti idėją ar išspręsti skubią problemą adresu Švietimo forumas kur tarptautiniu mastu susitinka šviežių minčių ir veiksmų švietimo taryba. Sukūrę dienoraštis, Jūs ne tik pagerinsite savo, kaip kompetentingo mokytojo, statusą, bet ir svariai prisidėsite prie ateities mokyklos kūrimo. Švietimo lyderių gildija atveria duris aukščiausio rango specialistams ir kviečia bendradarbiauti kuriant geriausias pasaulio mokyklas.
(
(Kadangi stačiakampiame trikampyje koja, esanti priešais 30 o kampą, yra lygi pusei hipotenuzės).
 savo srities būdai.
savo srities būdai.
(d 1 + d 2 = 140.
(d 1 2 + d 2 2 - d 1 d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 d 2 √2 = 144.
Norėdami gauti korepetitoriaus pagalbą – registruokitės.
Pirma pamoka nemokama!
Lygiagretainės savybės

BC = AD. O iš 1, 2, 3 ir 4 kampų lygybės išplaukia, kad kampas A = kampas1 + kampas3 = kampas2 + kampas4 = kampas C.
Pamokos tema
Pamokos tikslai
Pamokos tikslai
Pamokos planas
Įvadas

Lygiagretainio priešingų kraštinių savybės
Kadangi Δ AOB = Δ COD pagal pirmąjį trikampių lygybės ženklą (∠ AOB = ∠ COD, kaip vertikaliųjų, AO=OC, DO=OB, pagal lygiagretainių įstrižainių savybę), tai AB=CD. Panašiai iš trikampių BOC ir DOA lygybės išplaukia, kad BC=DA. Teorema įrodyta. Lygiagretainio priešingų kampų savybė
Tegu ABCD yra duotasis lygiagretainis. Ir tegul jos įstrižainės susikerta taške O.
Iš lygiagretainio priešingų kraštinių savybių, įrodytų teoremoje apie Δ ABC = Δ CDA iš trijų pusių (AB=CD, BC=DA iš įrodytosios, AC yra bendra). Iš trikampių lygybės išplaukia, kad ∠ABC = ∠CDA.
Taip pat įrodyta, kad ∠ DAB = ∠ BCD, kas išplaukia iš ∠ ABD = ∠ CDB. Teorema įrodyta.Lygiagretainio įstrižainių savybė
Pagal ankstesnę teoremą AB 1 CD yra lygiagretainis. Todėl tiesė AB 1 yra lygiagreti DC. Tačiau per tašką A lygiagrečiai DC gali būti nubrėžta tik viena linija. Vadinasi, tiesė AB 1 sutampa su tiese AB.
Taip pat įrodyta, kad BC 1 sutampa su BC. Taigi taškas C sutampa su C 1 . lygiagretainis ABCD sutampa su lygiagretainiu AB 1 CD. Todėl lygiagretainio įstrižainės susikerta, o susikirtimo taškas yra padalintas į pusę. Teorema įrodyta.
Aukščiau buvo įrodyta, kad susikirtimo taškas dalija įstrižaines – jei toks yra. Minėti samprotavimai jokiu būdu neįrodo jo egzistavimo. Tai yra, teoremos dalis „lygiagretainės įstrižainės susikerta“ lieka neįrodyta.
Klausimai
Naudotų šaltinių sąrašas