U ovom ćemo članku sveobuhvatno pogledati. Osnovni trigonometrijski identiteti su jednakosti koje uspostavljaju odnos između sinusa, kosinusa, tangensa i kotangensa jednog kuta i omogućuju vam da pronađete bilo koju od ovih trigonometrijskih funkcija kroz poznati drugi.
Odmah navodimo glavne trigonometrijske identitete koje ćemo analizirati u ovom članku. Zapisujemo ih u tablicu, au nastavku donosimo izvođenje ovih formula i dajemo potrebna objašnjenja.
Navigacija po stranici.
Odnos između sinusa i kosinusa jednog kuta
Ponekad se ne govori o glavnim trigonometrijskim identitetima navedenim u gornjoj tablici, već o jednom jedinom osnovni trigonometrijski identitet ljubazan ![]() . Objašnjenje ove činjenice je prilično jednostavno: jednakosti se dobivaju iz osnovnog trigonometrijskog identiteta nakon dijeljenja oba njegova dijela s i redom, a jednakosti
. Objašnjenje ove činjenice je prilično jednostavno: jednakosti se dobivaju iz osnovnog trigonometrijskog identiteta nakon dijeljenja oba njegova dijela s i redom, a jednakosti  i
i ![]() slijede iz definicija sinusa, kosinusa, tangensa i kotangensa. O tome ćemo detaljnije raspravljati u sljedećim paragrafima.
slijede iz definicija sinusa, kosinusa, tangensa i kotangensa. O tome ćemo detaljnije raspravljati u sljedećim paragrafima.
Odnosno, od posebnog je interesa jednakost koja je dobila naziv glavni trigonometrijski identitet.
Prije nego dokažemo osnovni trigonometrijski identitet, dat ćemo njegovu formulaciju: zbroj kvadrata sinusa i kosinusa jednog kuta identički je jednak jedan. Sada dokažimo.
Osnovni trigonometrijski identitet vrlo se često koristi u transformacija trigonometrijskih izraza. Omogućuje da se zbroj kvadrata sinusa i kosinusa jednog kuta zamijeni jedinicom. Ne manje često, osnovni trigonometrijski identitet koristi se obrnutim redoslijedom: jedinica se zamjenjuje zbrojem kvadrata sinusa i kosinusa bilo kojeg kuta.
Tangens i kotangens kroz sinus i kosinus
Identiteti koji povezuju tangens i kotangens sa sinusom i kosinusom jednog kuta oblika i ![]() neposredno proizlaze iz definicija sinusa, kosinusa, tangensa i kotangensa. Doista, po definiciji, sinus je ordinata od y, kosinus je apscisa od x, tangens je omjer ordinate i apscise, tj.
neposredno proizlaze iz definicija sinusa, kosinusa, tangensa i kotangensa. Doista, po definiciji, sinus je ordinata od y, kosinus je apscisa od x, tangens je omjer ordinate i apscise, tj. ![]() , a kotangens je omjer apscise i ordinate, tj.
, a kotangens je omjer apscise i ordinate, tj. ![]() .
.
Zbog te očitosti identiteta i ![]() često se definicije tangensa i kotangensa ne daju kroz omjer apscise i ordinate, već kroz omjer sinusa i kosinusa. Dakle, tangens kuta je omjer sinusa i kosinusa ovog kuta, a kotangens je omjer kosinusa i sinusa.
često se definicije tangensa i kotangensa ne daju kroz omjer apscise i ordinate, već kroz omjer sinusa i kosinusa. Dakle, tangens kuta je omjer sinusa i kosinusa ovog kuta, a kotangens je omjer kosinusa i sinusa.
Za kraj ovog odjeljka, treba napomenuti da su identiteti i ![]() vrijede za sve takve kutove za koje trigonometrijske funkcije u njima imaju smisla. Dakle, formula vrijedi za sve osim (inače će nazivnik biti nula, a nismo definirali dijeljenje s nulom), a formula
vrijede za sve takve kutove za koje trigonometrijske funkcije u njima imaju smisla. Dakle, formula vrijedi za sve osim (inače će nazivnik biti nula, a nismo definirali dijeljenje s nulom), a formula ![]() - za sve, različite od, gdje je z bilo koji.
- za sve, različite od, gdje je z bilo koji.
Odnos tangensa i kotangensa
Još očitiji trigonometrijski identitet od prethodna dva je identitet koji povezuje tangens i kotangens jednog kuta oblika ![]() . Jasno je da se to događa za sve kutove osim , inače ni tangens ni kotangens nisu definirani.
. Jasno je da se to događa za sve kutove osim , inače ni tangens ni kotangens nisu definirani.
Dokaz formule ![]() jako jednostavno. Po definiciji i odakle
jako jednostavno. Po definiciji i odakle  . Dokaz se mogao provesti i na malo drugačiji način. Od i
. Dokaz se mogao provesti i na malo drugačiji način. Od i ![]() , onda
, onda  .
.
Dakle, tangens i kotangens jednog kuta, u kojem imaju smisla, je.
Tema: Trigonometrijske formule (25 sati)
Lekcija 6 - 7: Odnos između sinusa, kosinusa i tangensa istog kuta.
Cilj: proučavati odnos između sinusa, kosinusa i tangensa istog kuta. Za postizanje ovog cilja potrebno je:
- Znati:
- formulacije definicija glavnih trigonometrijskih funkcija (sinus, kosinus i tangens); predznaci trigonometrijskih funkcija u četvrtinama; skup vrijednosti trigonometrijskih funkcija; osnovne formule trigonometrije.
- razumjeti:
- da se osnovni trigonometrijski identitet može koristiti samo za jedan te isti argument; algoritam za izračunavanje jedne trigonometrijske funkcije kroz drugu.
- primijeniti:
- sposobnost odabira prave formule za rješavanje određenog zadatka; sposobnost rada sa prosti razlomci; sposobnost izvođenja transformacije trigonometrijskih izraza.
- Analiza:
- analizirati pogreške u logici zaključivanja.
- Sinteza:
- ponuditi vlastiti način rješavanja primjera; izraditi križaljku koristeći se stečenim znanjem.
- Razred:
- znanja i vještine o ovoj temi za korištenje u drugim dijelovima algebre.
- Organiziranje vremena.
- Obnavljanje znanja i vještina.
- U kojoj je četvrtini kut od 1 radijana i čemu je približno jednak?
- Koja riječ nedostaje u definiciji funkcije sinus?
- Koja riječ nedostaje u definiciji kosinusne funkcije?
- Koje vrijednosti može uzeti sinus?
 ()
() - Objašnjenje novog gradiva.
 nacrtajmo jediničnu kružnicu sa središtem u točki O. Neka polumjer OB dobijemo okretanjem polumjera OA, jednakog R, za kut (slika 5). Zatim po definiciji
nacrtajmo jediničnu kružnicu sa središtem u točki O. Neka polumjer OB dobijemo okretanjem polumjera OA, jednakog R, za kut (slika 5). Zatim po definiciji 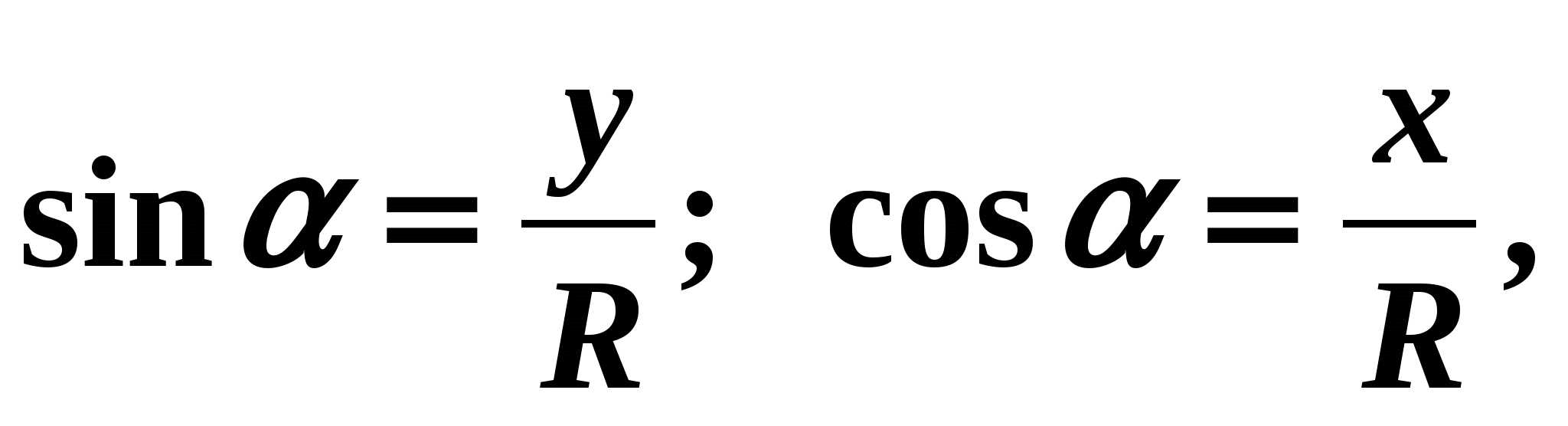 gdje
gdje 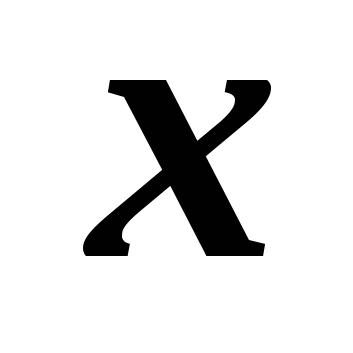 - apscisa točke B,
- apscisa točke B, 
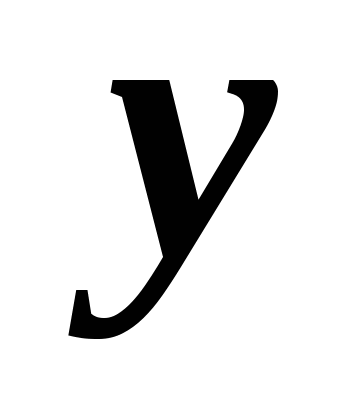 je njegova ordinata. Slijedi da točka B pripada kružnici. Stoga njegove koordinate zadovoljavaju jednadžbu
je njegova ordinata. Slijedi da točka B pripada kružnici. Stoga njegove koordinate zadovoljavaju jednadžbu 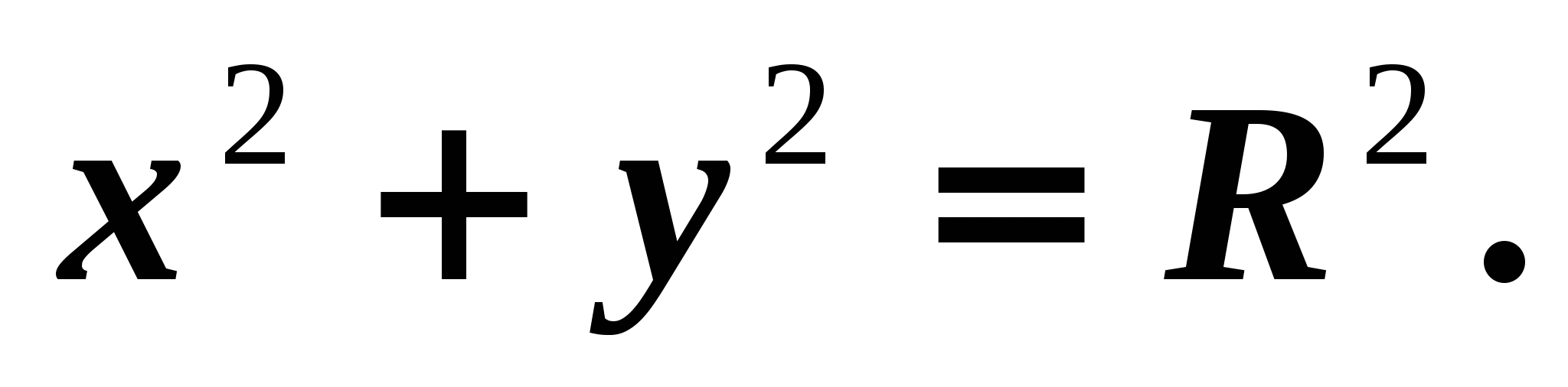 Koristeći ono što dobijemo
Koristeći ono što dobijemo  (1).
Dobili smo jednakost koja vrijedi za bilo koju vrijednost slova koja su u njoj uključena. Kako se zovu te jednakosti? Tako je – identiteti. Jednakost (1) se zove osnovni trigonometrijski identitet. U jednakosti (1) može poprimiti bilo koje vrijednosti. Dovršite sami snimku:
(1).
Dobili smo jednakost koja vrijedi za bilo koju vrijednost slova koja su u njoj uključena. Kako se zovu te jednakosti? Tako je – identiteti. Jednakost (1) se zove osnovni trigonometrijski identitet. U jednakosti (1) može poprimiti bilo koje vrijednosti. Dovršite sami snimku: 1.
Provjerite je li vaš unos točan. Stavite si bodove na karticu lekcije za Zadaci broj 2. Nastavljamo. Izveli smo osnovni trigonometrijski identitet, ali zašto nam treba? Tako je - pronaći vrijednost kosinusa iz jedne poznate vrijednosti sinusa i obrnuto. Sada uvijek možemo koristiti osnovni trigonometrijski identitet, ali glavna stvar je za isti argument. Učenici se u bilježnici pozivaju da iz osnovnog trigonometrijskog identiteta samostalno izraze sinus kroz kosinus i kosinus kroz sinus. Dva učenika su pozvana pred ploču da provjere. Jedan je pozvan da izrazi sinus kroz kosinus, drugi - kosinus kroz sinus. Točan odgovor je prikazan na ekranu:
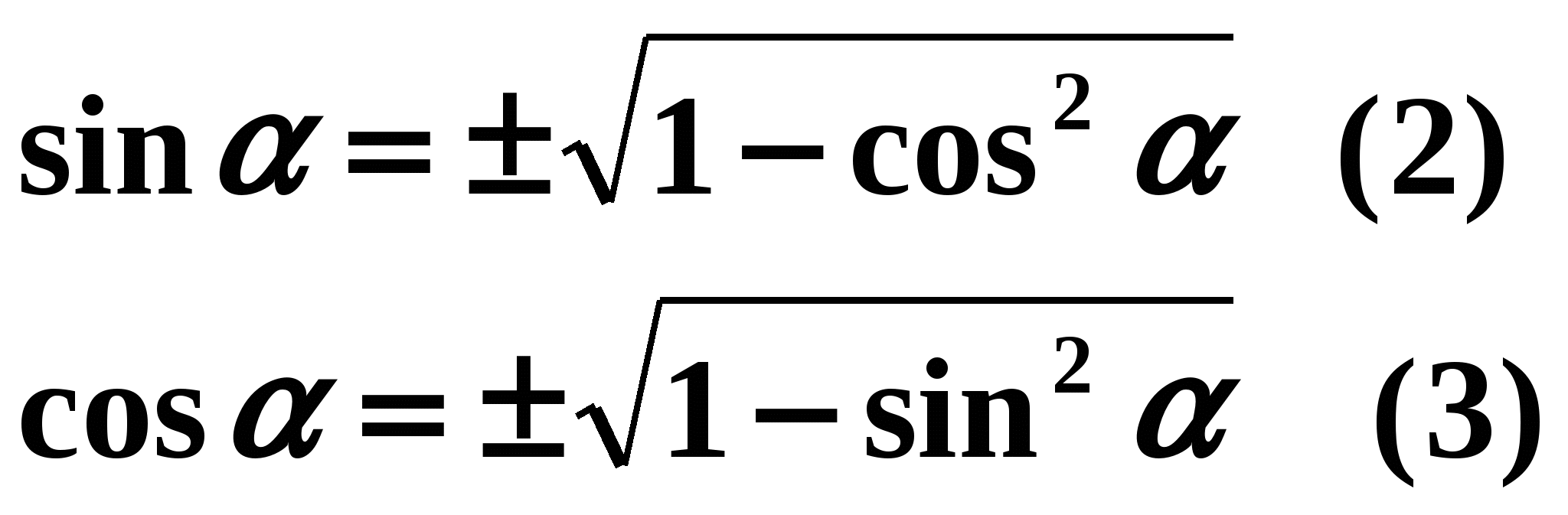 Učenici provjeravaju svoje odgovore i bodove na kartici lekcije za Zadaci broj 3.
O čemu u ovim formulama ovisi znak ispred korijena? (Na kojoj se četvrtini nalazi kut trigonometrijske funkcije koju definiramo).
Učenici provjeravaju svoje odgovore i bodove na kartici lekcije za Zadaci broj 3.
O čemu u ovim formulama ovisi znak ispred korijena? (Na kojoj se četvrtini nalazi kut trigonometrijske funkcije koju definiramo). Primjer 1 . Izračunati
 ako
ako 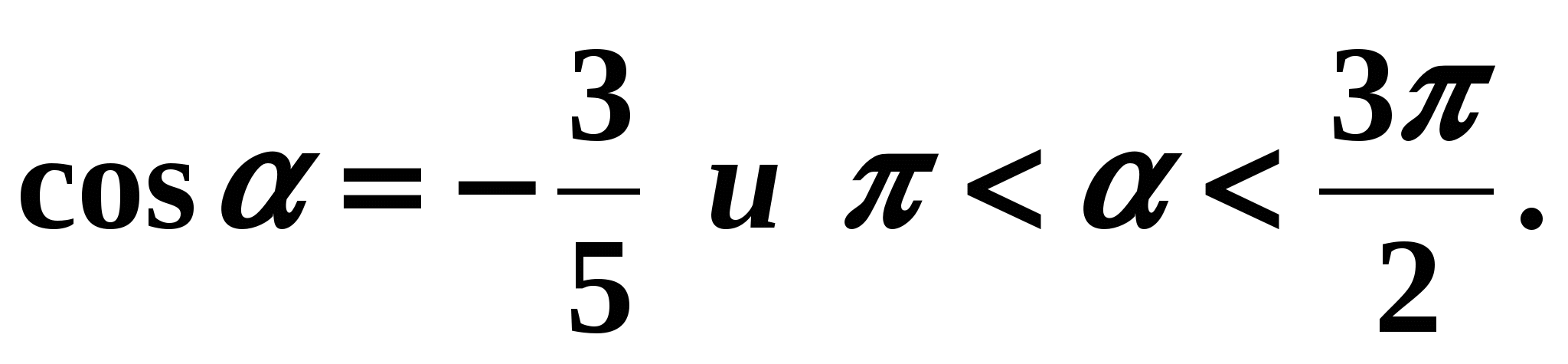 Odredi četvrtinu u kojoj se kut nalazi
Odredi četvrtinu u kojoj se kut nalazi  . Četvrt - III. Podsjetimo da je sinus u trećoj četvrtini negativan, tj. u formuli (2) trebate staviti znak "-" ispred korijena: Primjer 2
Izračunati
. Četvrt - III. Podsjetimo da je sinus u trećoj četvrtini negativan, tj. u formuli (2) trebate staviti znak "-" ispred korijena: Primjer 2
Izračunati 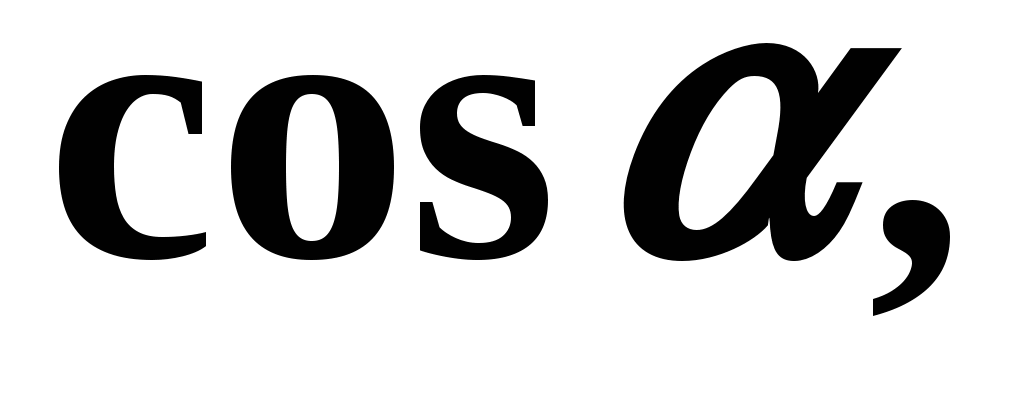 ako
ako  Odredimo četvrtinu u kojoj se nalazi kut . Četvrtina - IV, kosinus u četvrtoj četvrtini je pozitivan. Stoga je u formuli (3) prije korijena potreban znak "+":
Odredimo četvrtinu u kojoj se nalazi kut . Četvrtina - IV, kosinus u četvrtoj četvrtini je pozitivan. Stoga je u formuli (3) prije korijena potreban znak "+": Saznajte sada odnos između tangensa i kotangensa. Po definiciji tangensa i kotangensa
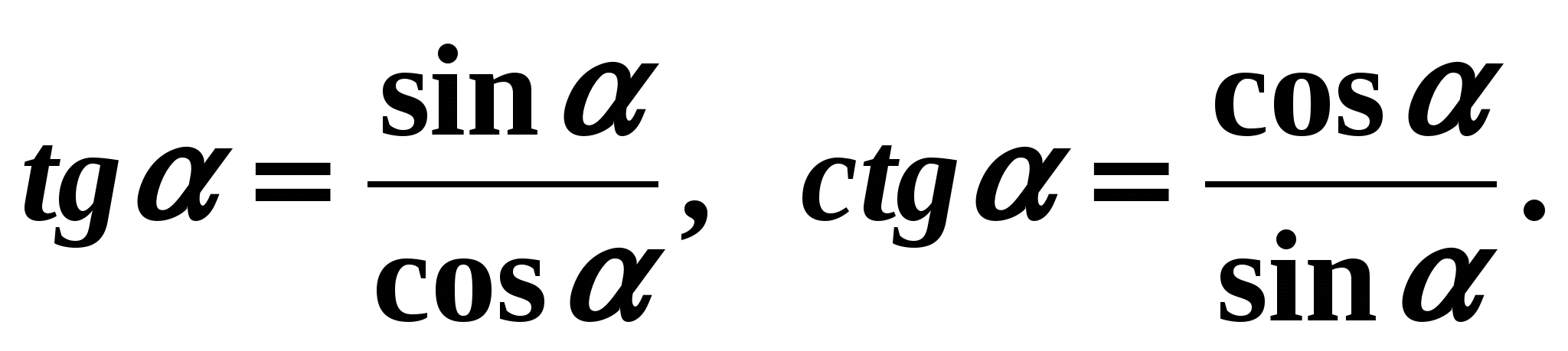
Množenjem ovih jednakosti dobivamo:

Iz jednakosti (4) možemo izraziti
 kroz
kroz  i obrnuto:
i obrnuto: 
Jednakosti (4) - (6) vrijede za sve vrijednosti za koje
 imati smisla, tj. kada
imati smisla, tj. kada 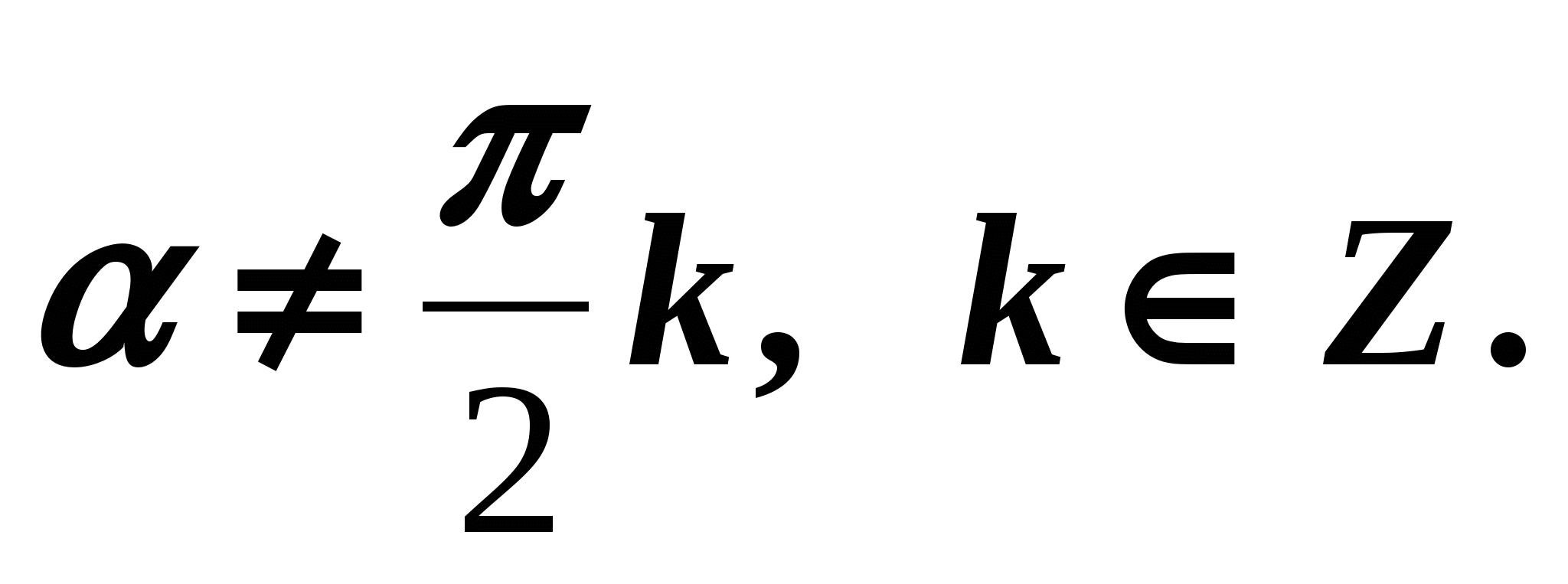 Sada izvodimo formule koje izražavaju odnos između tangensa i kosinusa, kao i kotangensa i sinusa istog argumenta. Dijeljenje obje strane jednakosti (1) sa
Sada izvodimo formule koje izražavaju odnos između tangensa i kosinusa, kao i kotangensa i sinusa istog argumenta. Dijeljenje obje strane jednakosti (1) sa 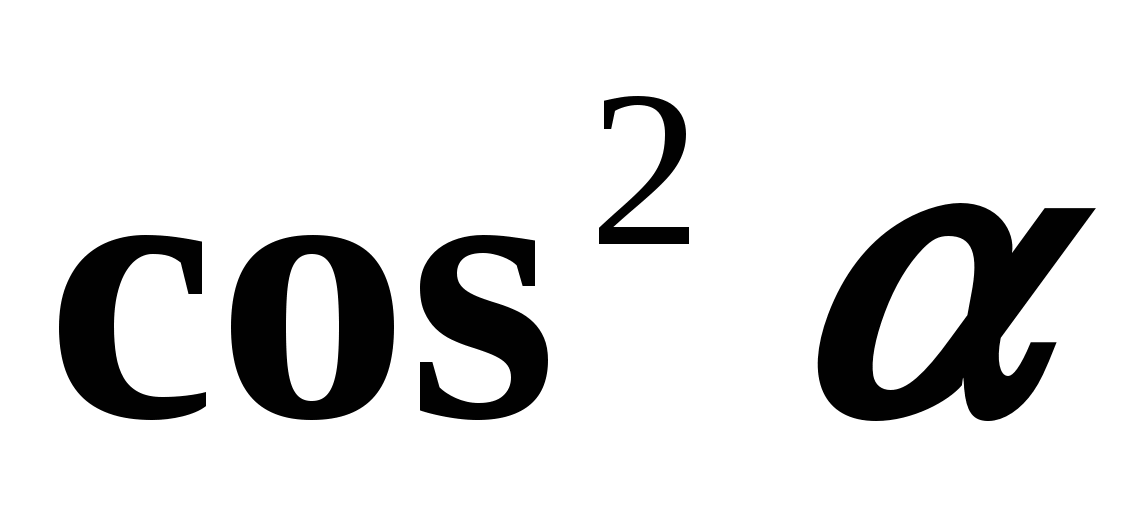 , dobivamo:
, dobivamo:  oni.
oni. 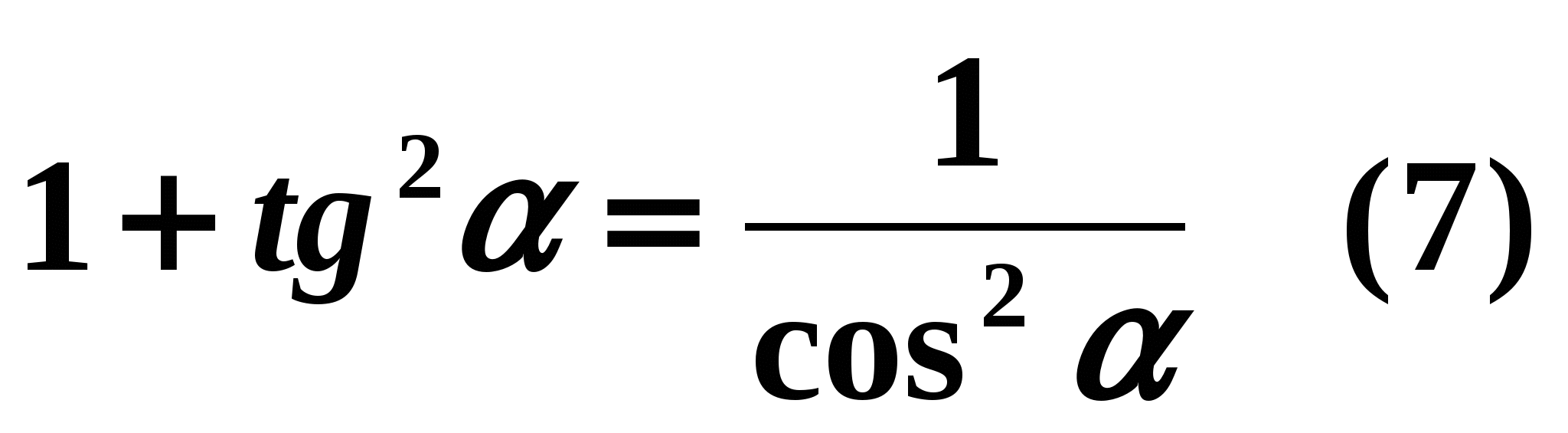
Ako se oba dijela jednakosti (1) podijele sa
 , onda ćemo imati:
, onda ćemo imati: 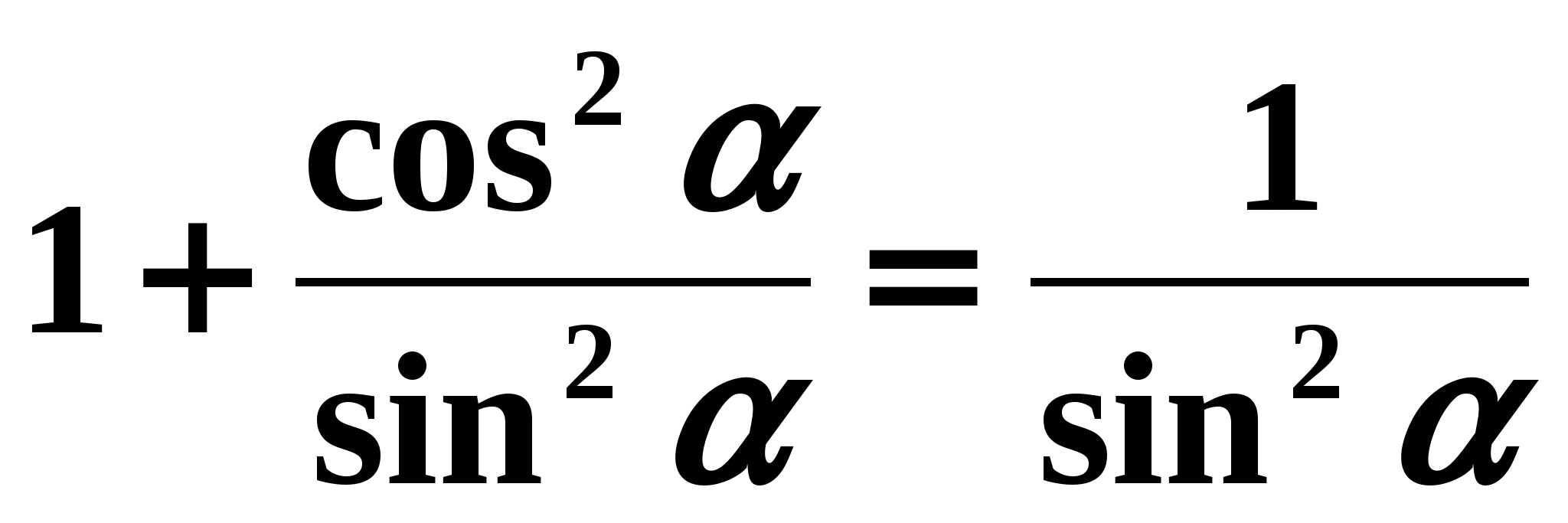 oni.
oni. 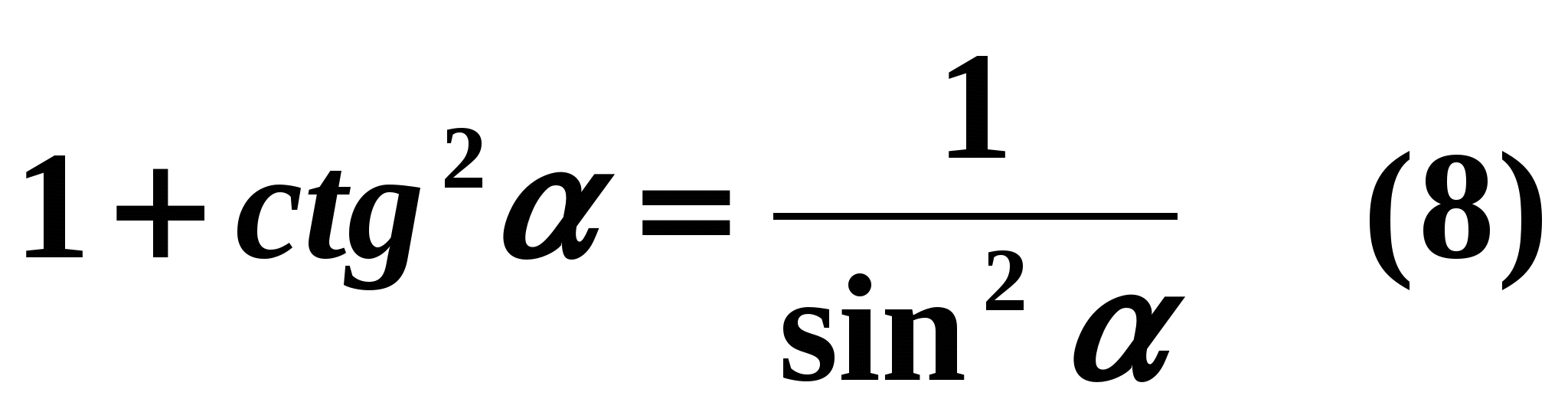
Razmotrite primjere korištenja izvedenih formula za pronalaženje vrijednosti trigonometrijskih funkcija poznata vrijednost jedan od njih.
Primjer 1 Pronađi ako to znamo
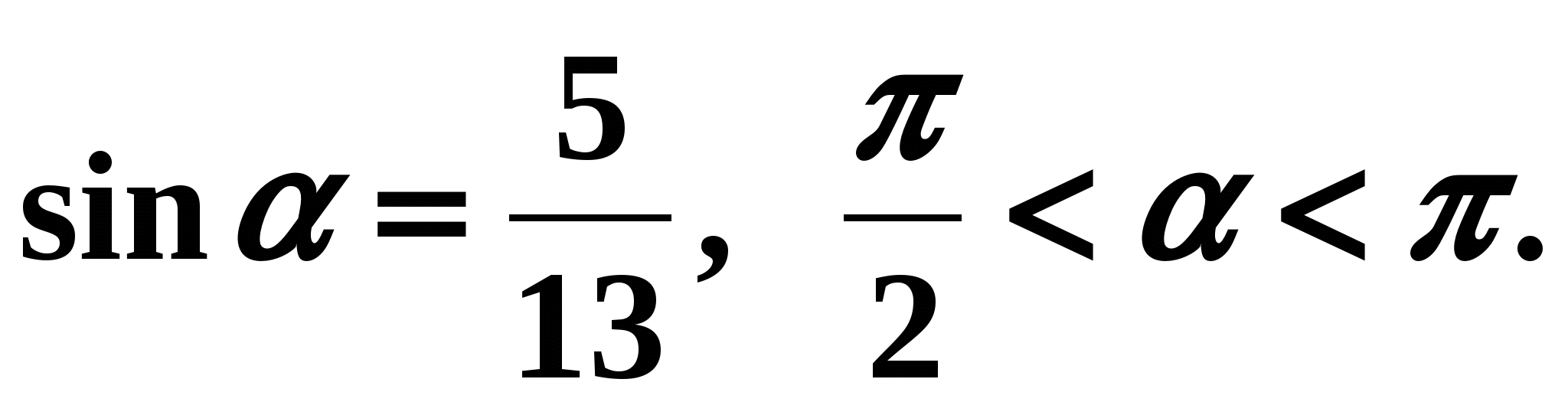 Odluka:
Odluka: 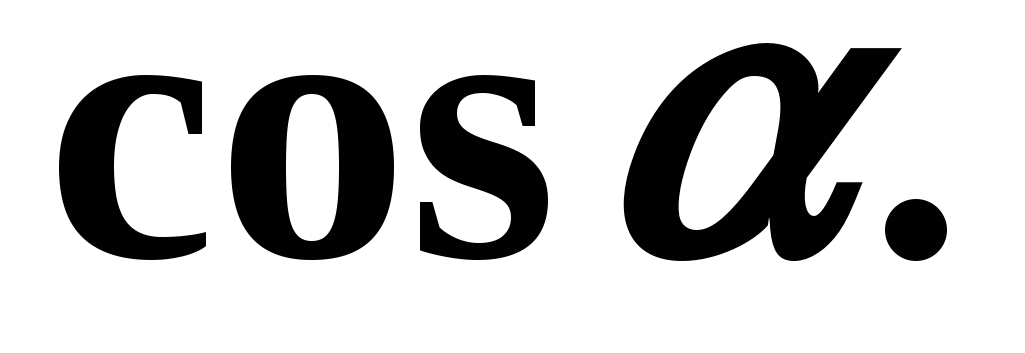
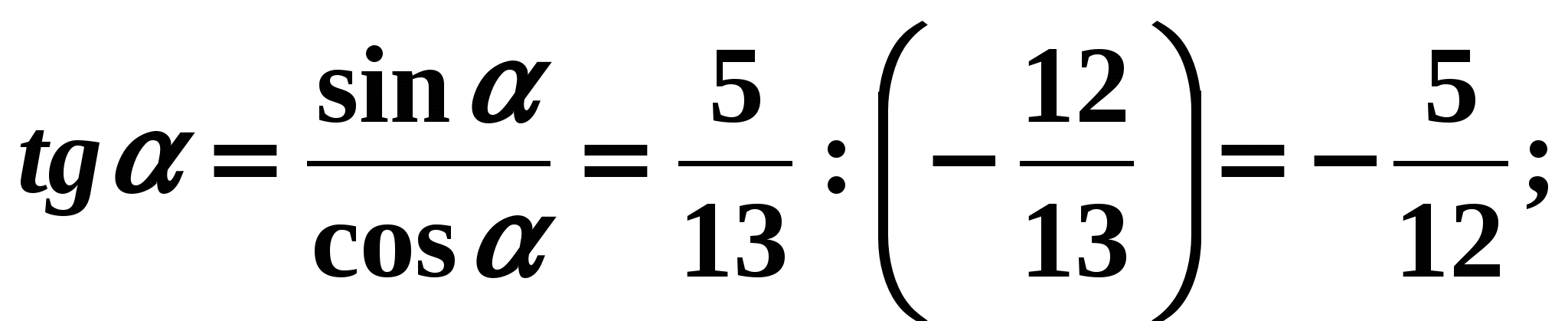
- Za pronalaženje kotangensa kuta prikladno je koristiti formulu (6):
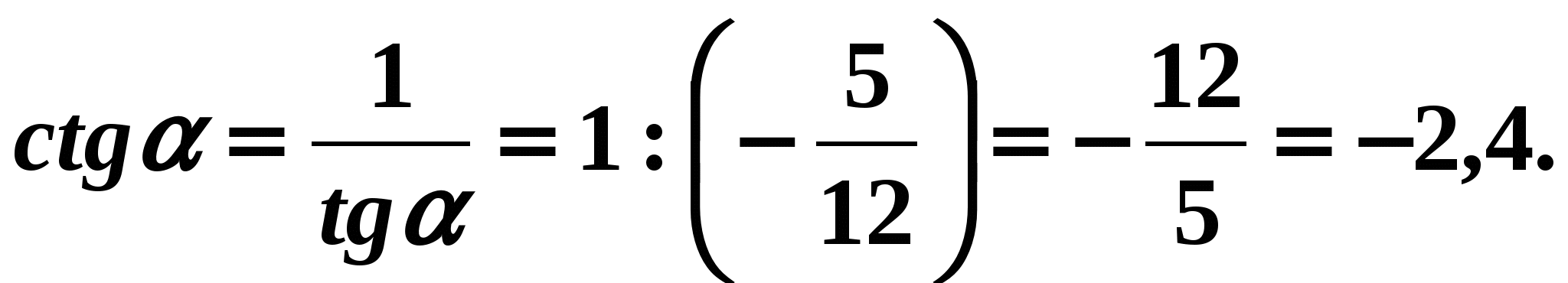 Odgovor:
Odgovor: Primjer2. Poznato je da
 . Pronađite sve ostale trigonometrijske funkcije. Odluka:
. Pronađite sve ostale trigonometrijske funkcije. Odluka: - Upotrijebimo formulu (7).
Imamo:

 ,
,  . Prema uvjetu zadatka, kut je kut od 1 četvrtine, pa je njegov kosinus pozitivan. Sredstva
. Prema uvjetu zadatka, kut je kut od 1 četvrtine, pa je njegov kosinus pozitivan. Sredstva 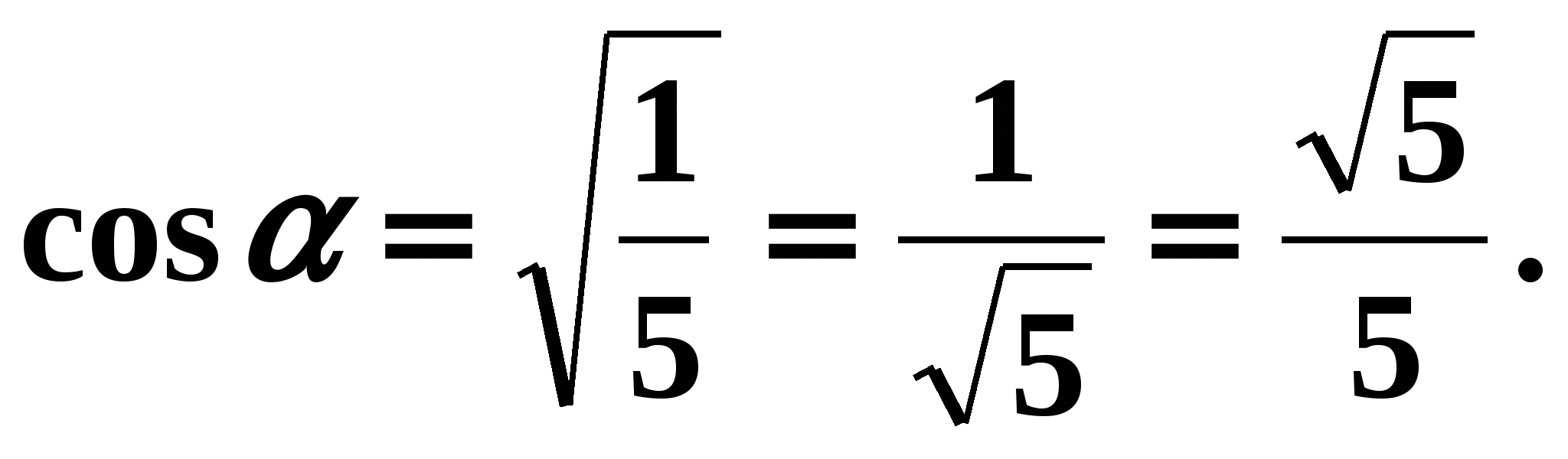

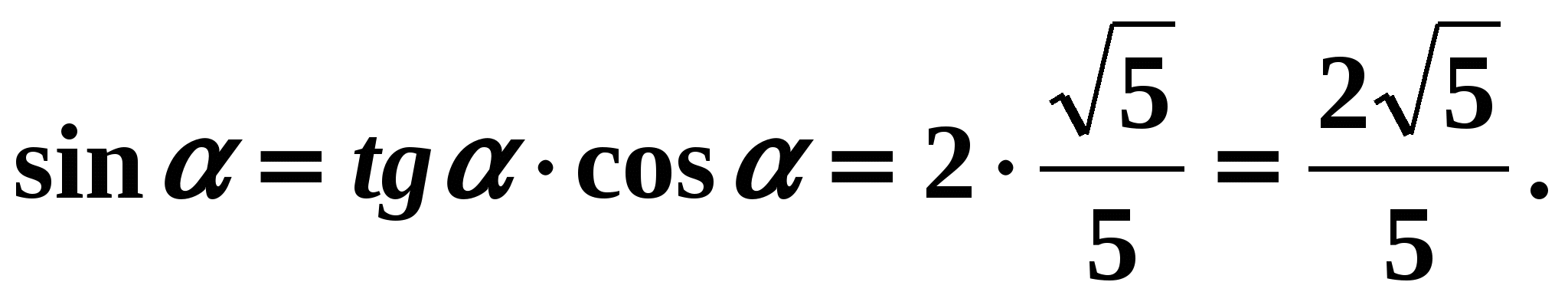
Odgovor:
 Uspostavljeni odnosi između trigonometrijskih funkcija istog argumenta omogućuju pojednostavljenje trigonometrijskih izraza.
Uspostavljeni odnosi između trigonometrijskih funkcija istog argumenta omogućuju pojednostavljenje trigonometrijskih izraza. Primjer 3 Pojednostavimo izraz:
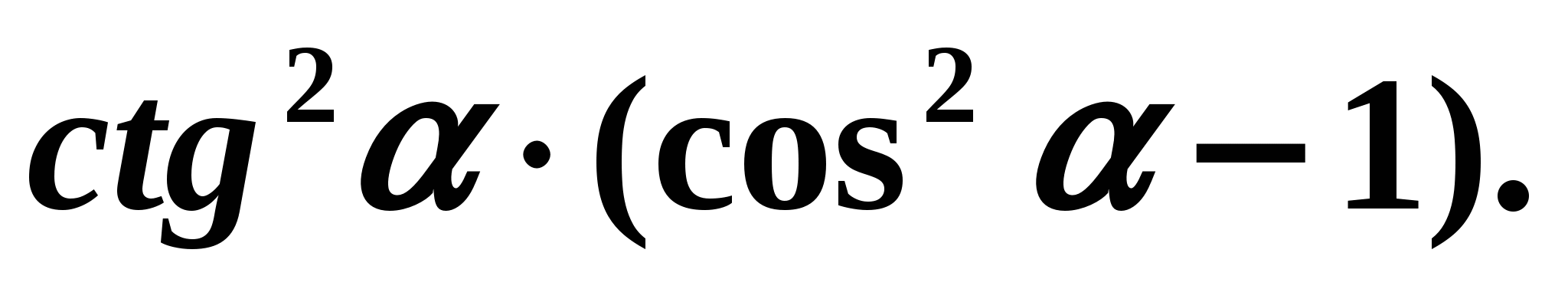 Odluka: Poslužimo se formulama:
Odluka: Poslužimo se formulama: 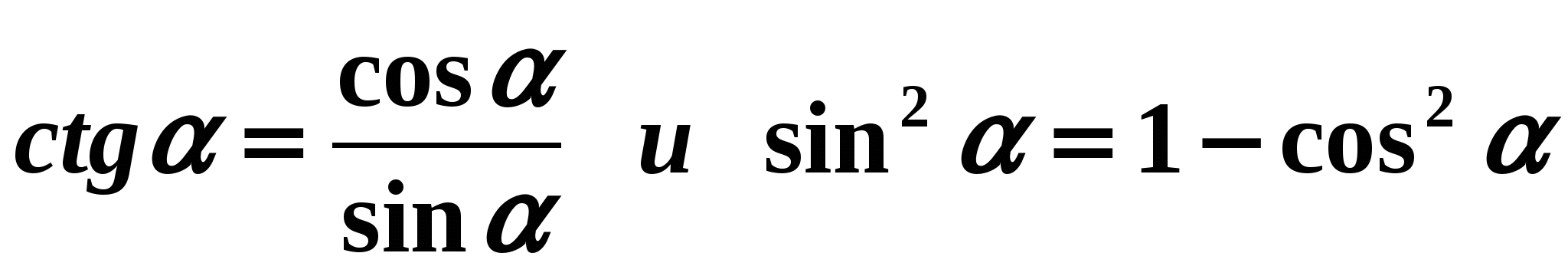 . Dobivamo:
. Dobivamo: - Konsolidacija.
A sada su na ekranu rubrike samoprocjene na ovu temu. Označite koju biste razinu željeli dosegnuti danas.
Razumijem temu i mogu rješavati primjere algoritmom, gledajući u bilježnicu, ali uz pomoć sugestivna pitanja(kartica - uputa).
Razumijem temu i mogu rješavati primjere pomoću algoritma, gledajući u bilježnicu, koristeći upute nastavnika.
Razumio sam temu i mogu rješavati primjere pomoću algoritma, gledajući u bilježnicu, bez sugestivnih pitanja i uputa.
Razumio sam temu i mogu rješavati primjere pomoću algoritma bez gledanja u bilježnicu.
Koju god razinu odabrali, prvo pažljivo pregledaj sve zadatke koje sam ti dao, a zatim ispuni zadatak koji odgovara razini koju si odabrao (pred tobom su zadaci od četiri opcije, broj opcije odgovara razinama samo procjena.)
1 opcija
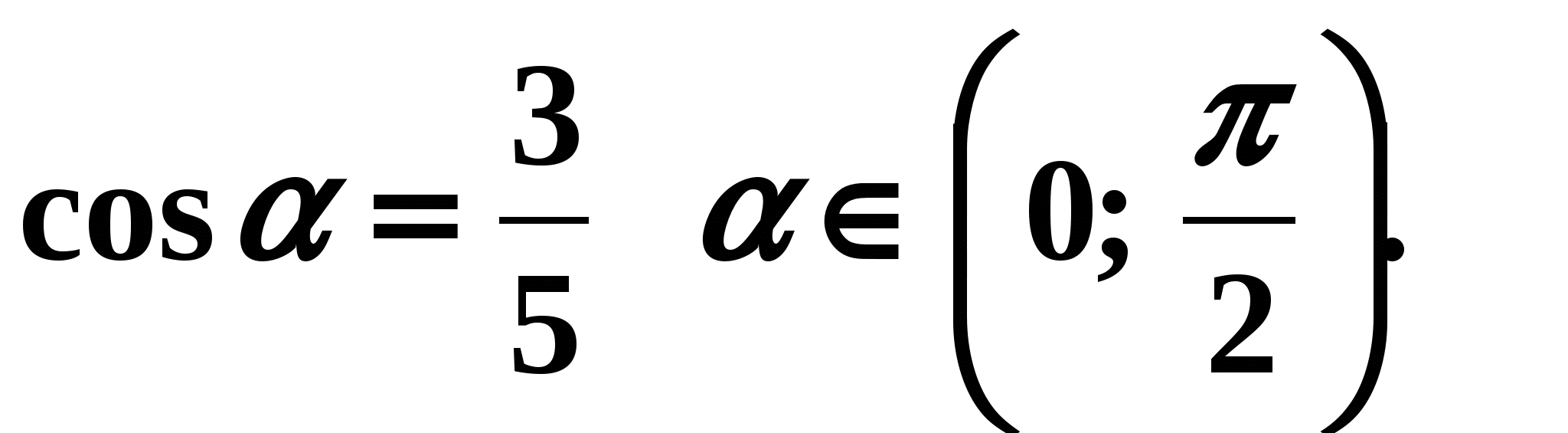 Uputa:
Uputa:
4 opcija
Sada dečki, provjerimo odgovore. Točni odgovori prikazani su na ekranu, a učenici provjeravaju svoj rad i upisuju bodove u karticu lekcije Zadaci broj 4. Procijenite se na karti lekcije. Izračunajte svoje rezultate i stavite ih na karticu.
- Domaća zadaća.
- Sve izvedene formule zapišite u priručnik. Prema udžbeniku br. 459 (3, 5), br. 460 (1)
Pokušajmo pronaći odnos između glavnih trigonometrijskih funkcija istog kuta.
Odnos između kosinusa i sinusa istog kuta
Sljedeća slika prikazuje Oxy koordinatni sustav u kojem je prikazan dio jedinične polukružnice ACB sa središtem u točki O. Taj dio je luk jedinične kružnice. Jedinična kružnica opisana je jednadžbom
- x2+y2=1.
Kao što je već poznato, ordinata y i apscisa x mogu se prikazati kao sinus i kosinus kuta pomoću sljedećih formula:
- sin(a) = y,
- cos(a) = x.
Zamjenom ovih vrijednosti u jednadžbe jediničnog kruga, imamo sljedeću jednakost
- (sin(a)) 2 + (cos(a)) 2 =1,
Ova jednakost vrijedi za sve vrijednosti kuta a. Naziva se osnovnim trigonometrijskim identitetom.
Iz osnovnog trigonometrijskog identiteta, jedna se funkcija može izraziti pomoću druge.
- sin(a) = ±√(1-(cos(a)) 2),
- cos(a) = ±√(1-(sin(a)) 2).
Predznak na desnoj strani ove formule određen je predznakom izraza na lijevoj strani ove formule.
Na primjer.
Izračunajte sin(a) ako je cos(a)=-3/5 i pi Upotrijebimo gornju formulu: Od pi Sada pokušajmo pronaći odnos između tangensa i kotangenata. Prema definiciji, tg(a) = sin(a)/cos(a), ctg(a) = cos(a)/sin(a). Množenjem ovih jednakosti dobivamo tg(a)*ctg(a) =1. Iz ove jednakosti jedna se funkcija može izraziti pomoću druge. Dobivamo: Treba razumjeti da ove jednakosti vrijede samo kada tg i ctg postoje, to jest za bilo koji a, osim za a = k * pi / 2, za bilo koji cijeli broj k. Pokušajmo sada upotrijebiti osnovni trigonometrijski identitet da pronađemo odnos između tangensa i kosinusa. Podijelite osnovni trigonometrijski identitet s (cos(a)) 2 . (cos(a) nije jednak nuli, inače tangens ne bi postojao. Dobivamo sljedeću jednakost ((sin(a)) 2 + (cos(a)) 2)/ (cos(a)) 2 =1/(cos(a)) 2 . Dijeleći pojam po pojam dobivamo: Kao što je gore navedeno, ova je formula istinita ako cos(a) nije jednak nuli, to jest, za sve kutove a, osim a=pi/2 + pi*k, za bilo koji cijeli broj k. Sinusni grafikon val po val Iz đačke pjesme. CILJEVI I ZADACI SATA: ŠTEDNJA ZDRAVLJA: stvaranje ugodne psihološke klime u razredu, atmosfera suradnje: učenik – učitelj. METODIČKA OPREMA SATA: MATERIJALNO TEHNIČKA BAZA: Kabinet matematike. DIDAKTIČKA POTPORA NASTAVNOG SATA: udžbenik, bilježnica, plakati na temu sata, tablice, računalo, diskovi, platno, projektor. METODE AKTIVNOSTI: grupni i individualni rad za stolom i pločom. VRSTA SATA: sat svladavanja novih znanja. TIJEKOM NASTAVE 1. Organizacijski trenutak: pozdrav, provjera prisutnosti učenika, popunjavanje dnevnika. 2. Provjera spremnosti učenika za nastavu: postavljanje učenika na rad, donošenje plana nastave. 3. Analiza pogrešaka u domaćim zadaćama. Na ekranu - slika s točno ispunjenom domaćom zadaćom. Svaki učenik detaljnim frontalnim objašnjenjem provjerava i bilježi pravilnost provedbe u radnoj kartici sata. RADNA LEKCIJA. C / o - samopoštovanje. O / t - procjena prijatelja. 4. Aktualizacija znanja, priprema za percepciju novog materijala. Sljedeća faza naše lekcije je diktat. Odgovore ukratko zapisujemo – crtež je na našem slajdu. Diktat (usmeno ponavljanje potrebnih podataka): 1. Definirajte: 2. Definirajte: 3. Zapiši predznake sinusa, kosinusa, tangensa, kotangensa za kutove dobivene okretanjem točke P (1; 0) za kut 4. Za sve ove kutove označite četvrtine koordinatne ravnine. Dečki provjeravaju diktat na slajdu zajedno s učiteljem, objašnjavajući svaku izjavu i ocjenjujući se na radnom listu lekcije. 5. Iz povijesti trigonometrije. Suvremeni oblik trigonometrije dao je najveći matematičar 18. stoljeća Leonhard Euler- Podrijetlom Švicarac, koji je godinama radio u Rusiji i bio član Peterburške akademije znanosti. Uveo je poznate definicije trigonometrijskih funkcija, formulirao i dokazao redukcijske formule s kojima se tek treba upoznati, razlikovao klase parnih i neparnih funkcija. 6. Uvođenje novog gradiva: Glavno je ne samo obavijestiti studente o konačnim zaključcima, nego ih učiniti takoreći sudionicima znanstvenog traganja: postavljanjem pitanja, tako da se i oni, probudivši svoju znatiželju, uključe u studiju. , što doprinosi postizanju višeg stupnja mentalnog razvoja učenika. Stoga pri uvođenju novog gradiva stvaram problematičnu situaciju - kako lakše i racionalnije utvrditi odnos između sinusa i kosinusa istog kuta - kroz jednadžbu jedinične kružnice ili kroz Pitagorin poučak. Razred je podijeljen na opcije za prvu i drugu opciju - na ekranu je slajd s uvjetom i crtežima, rješenja još nema. Opcija 1 uspostavlja odnos između sinusa i kosinusa kroz jednadžbu kruga sa središtem u ishodištu i polumjerom jednakim 1x 2 +y 2 =1; sin 2 + cos 2 =1. Opcija 2 uspostavlja odnos između sinusa i kosinusa kroz Pitagorin teorem - u pravokutnom trokutu, kvadrat hipotenuze jednak je zbroju kvadrata nogu: OB 2 + AB 2 \u003d OA 2 - i dobivamo sin 2 + cos 2 \u003d 1. Uspoređuju rezultate, izvlače zaključke: glavna stvar je jednakost ispunjena za sve vrijednosti slova uključenih u nju? Učenici moraju odgovoriti da je to isto (na slajdu je prikazano točno rješenje i za prvu i za drugu opciju). Dobili smo jednakost koja vrijedi za bilo koju vrijednost slova koja su u njoj uključena. Kako se zovu te jednakosti? Tako je – identiteti. Prisjetimo se - koje još identitete poznajemo u algebri - formule za skraćeno množenje: a 2 -b 2 \u003d (a-b) (a + b), (a-b) 2 \u003d a 2 -2ab + b 2 , (a+b) 3 =a 3 +3a 2 b+3ab 2 +b 2 , (a-b) 3 =a 3 -3a 2 b+3ab 3 -b 3 , a 3 -b 3 \u003d (a-b) (a 2 + ab + b 2), a 3 + b 3 \u003d (a + b) (a 2 -ab + b 2). Sljedeći problem - zašto smo izveli glavni trigonometrijski identitet - sin 2 + cos 2 =1. Tako je - pronaći jednu poznatu vrijednost sinusa, kosinusa ili tangensa - vrijednosti svih ostalih funkcija. Sada uvijek možemo koristiti osnovni trigonometrijski identitet, ali glavna stvar je za isti argument. Primjena stečenog znanja: OPCIJA 1 - Izrazite sinus preko kosinusa kuta. Opcija 2 - Izrazite kosinus kroz sinus kuta. Točan odgovor je na slajdu. Pitanje učiteljice - nitko nije zaboravio staviti znak + i -? Koji bi mogao biti kut? - bilo tko. O čemu u ovim formulama ovisi znak ispred korijena? na kojoj se četvrtini nalazi kut (argument) trigonometrijske funkcije koju definiramo. Za ploču izvodimo 2 učenika br.457. - 1. opcija - 1, 2. opcija - 2. Slajd prikazuje točan odgovor. Samostalan rad na prepoznavanju temeljnog trigonometrijskog identiteta 1. pronađite vrijednost izraza: 2. izrazi broj 1 kroz kut a, ako Postoji međusobna provjera – prema gotovom slajdu i vrednovanju rada – kako samoprocjenom tako i procjenom prijatelja. 6. Konsolidacija novog materijala (prema tehnologiji G.E. Khazankina - tehnologija pomoćnih zadataka). ZADATAK 1. Izračunajte ……….. ako je ……………………………………………………………………. 1 učenik samostalno za pločom – zatim slajd s točnim rješenjem. ZADATAK 2. Izračunajte……………., ako………………………………………………………………….. 2. učenik za pločom, zatim slajd s točnim rješenjem. 7. Tjelesni odgoj.Znam da ste već odrasli i mislite da niste nimalo umorni, pogotovo sada, kada je nastava toliko aktivna da nam se vrijeme kao da se produljuje – prema teoriji relativnosti A. Einsteina, ali napravimo gimnastiku za cerebralne žile: Otkrijmo sada odnos između tangensa i kotangensa………………………………………………………………………………………………………… ……… Postoji nova studija na temu - koliki može biti kut u drugom trigonometrijskom identitetu? GLAVNO JE TRAŽENJE SKUPA NA KOJEM SE TE JEDNAKOSTI PROVODE. OZNAČI NA SLICI TOČKE U KOJIMA NE POSTOJI TANGENTA I KOTENGENTA KUTA. 3. učenik za pločom. Jednakosti vrijede za …………………………. ZADATAK3. Izračunaj……… ako…………………………. ZADATAK 4. Izračunajte…………….. ako ………………………………………………………………… Ostali učenici rade u svojim bilježnicama. 1 PODRŠKA……………………………………………………………………………………………………… 2 PODRŠKA…………………………………………………………………………………………………… 3 PODRŠKA. Primjena osnovnog trigonometrijskog identiteta na rješavanje problema. 8. Križaljka. Anatole France jednom je rekao: "Učenje bi trebalo biti zabavno... Da biste probavili znanje, morate ga apsorbirati s apetitom." Kako biste provjerili svoje znanje o ovoj temi, nudi vam se križaljka. Nakon provjere križaljke, dečki si daju ocjene u radnu karticu lekcije. Nastavnik ocjenjuje one učenike koji su posebno aktivni na satu. Rezultat je prosječna ocjena za rad u lekciji. 9. Upućivanje učitelja na izradu domaće zadaće. 10. Sažetak lekcije od strane nastavnika. 11. Domaća zadaća: paragraf 25 (prije zadatka 5), br. 459 (parni), 460 (parni), 463 * (4). Udžbenik Sh.A Alimov "Algebra i početak analize", 10-11, "Prosvjetljenje", M., 2005. KARTA LEKCIJE "OVISNOST IZMEĐU SINUSA, KOSINUSA I TANGENA ISTOG KUTOVA" Student ________________________________________________________________________________ 1. Znam gradivo iz prethodnih lekcija Bodovi Odgovorio sam točno na sva pitanja bez obrisa. Odgovorio sam bez sinopsisa s jednom greškom. Odgovorio sam bez okvira i napravio više od jedne pogreške. Na sva pitanja točno sam odgovorio pomoću sažetka. Odgovorio sam sažeto, s jednom greškom Odgovorio sam koristeći sažetak i napravio više od jedne pogreške 2. Završio sam snimanje primjera Bodovi Sve sam zadatke obavio bez greške Završio sam s jednom greškom Izvršio sam zadatke i napravio više od dvije greške 3. Završio sam izvođenje formule za nalaženje sinusa i kosinusa Bodovi Shvatio sam formulu Zaključio sam formule i napravio jednu grešku Formule sam zaključio uz pomoć učitelja 4. Svoje znanje iz teme: "Odnos sinusa, kosinusa i tangensa istog kuta" primijenila sam pri rješavanju samostalnog rada. Bodovi Primjere opcije 1 sam riješio bez greške. Riješio sam primjere opcije 1 i pogriješio. Riješio sam primjere 2 opcije bez grešaka. Riješio sam primjere 2 opcije i pogriješio. Riješio sam primjere 3 opcije bez greške Riješio sam primjere 3 opcije i pogriješio. Riješio sam primjere 4 opcije bez greške. Riješio sam primjere 4 opcije i pogriješio. 5. Ocijenite sebe: Razumio sam izvođenje formula i mogu riješiti primjere na ovu temu uz bilježnicu i uz pomoć učitelja. Razumio sam izvođenje formula i mogu sam rješavati primjere bez bilježnice, samo gledajući formule. Razumio sam izvođenje formula i mogu sam rješavati primjere bez bilježnice, ako zaboravim formulu, mogu je sam zaključiti. Moji rezultati: __________ Maksimalni broj bodova - 22 18 - 22 boda - ocjena "5" 15 - 17 bodova - ocjena "4" 11–14 bodova - ocjena "3" Manje od 11 bodova - trebate doći na konzultacije u narednim danima, gradivo još nije savladano. Golovatova Vera Anatolyevna, učiteljica matematike GB POU "Okhta College" Sažetak dviju lekcija za studenteja
tečaj (10kl.) na temu: "Odnos između sinusa, kosinusa i tangensa istog kuta" Cilj: proučavati odnos između sinusa, kosinusa i tangensa istog kuta. Za postizanje ovog cilja potrebno je: Znati: formulacije definicija glavnih trigonometrijskih funkcija (sinus, kosinus i tangens); predznaci trigonometrijskih funkcija u četvrtinama; skup vrijednosti trigonometrijskih funkcija; osnovne formule trigonometrije. razumjeti: da se osnovni trigonometrijski identitet može koristiti samo za jedan te isti argument; algoritam za izračunavanje jedne trigonometrijske funkcije kroz drugu. primijeniti: sposobnost odabira prave formule za rješavanje određenog zadatka; sposobnost rada s jednostavnim razlomcima; sposobnost izvođenja transformacije trigonometrijskih izraza. Analiza: analizirati pogreške u logici zaključivanja. Sinteza: ponuditi vlastiti način rješavanja primjera; izraditi križaljku koristeći se stečenim znanjem. Razred: znanja i vještine o ovoj temi za korištenje u drugim dijelovima algebre. Oprema:
izgled trigonometrijske kružnice, brošure s formulama i tablicama vrijednosti trigonometrijskih funkcija, računalo, multimedijski projektor, prezentacija, radni listovi za samostalno učenje. Korišteni izvori: Algebra i počeci analize: udžbenik za 10.-11. opće obrazovanje institucije / Sh.A. Alimov, Yu.V. Sidorov i dr. Obrazovanje, 2006. Zadaci Otvorene banke za pripremu ispita iz matematike, 2011 Internet resursi. Kratki plan lekcije: Organiziranje vremena. Lijepi pozdrav. Priopćavanje svrhe sata i plana rada na satu - 3-5 min. Obnavljanje znanja i vještina. Učenici dobivaju kartice lekcija i objašnjava im se kako s njima raditi. Pitanja se prikazuju na ekranu; učenici svoje odgovore zapisuju u bilježnicu; Učitelj prikazuje točan odgovor na ekranu. Nakon završetka ankete učenici upisuju bodove u nastavnu karticu za Zadaci broj 1
– 10 minuta. Objašnjenje novog gradiva. Nastavnik izvodi formulu za osnovni trigonometrijski identitet - 5 minuta. Učenici se pozivaju da samostalno dovrše snimku primjera prikazanih na ekranu, provjere točnost odgovora i stave bodove na karticu lekcije za Zadaci broj 2 -
5 minuta. Učenici se u bilježnici pozivaju da iz osnovnog trigonometrijskog identiteta samostalno izraze sinus kroz kosinus i kosinus kroz sinus. Točan odgovor je prikazan na ekranu, učenici provjeravaju i stavljaju bodove na karticu lekcije za Zadaci №3
– 5-7 min. Učitelj na ploči rješava primjere o primjeni osnovnog trigonometrijskog identiteta. Učenici odgovaraju na pitanja nastavnika dok objašnjavaju i zapisuju primjere u svoje bilježnice – 15 minuta. Nastavnik izvodi formule koje pokazuju odnos tangensa i kotangensa, učenici aktivno sudjeluju u izvođenju formula, odgovaraju na pitanja i bilježe u bilježnicu - 5 minuta. Učitelj izvodi formule koje pokazuju odnos između tangensa i kosinusa, između sinusa i kotangensa - 5 minuta. Učenici se pozivaju pred ploču po želji i uz pomoć učitelja rješavaju primjere pomoću algoritma. Svi ostali vode bilješke i odgovaraju na pitanja po potrebi – 10 minuta. Konsolidacija proučavanog materijala Na kraju lekcije na ekranu se prikazuju točni odgovori, učenici provjeravaju svoje odgovore i stavljaju bodove na karticu lekcije za Zadaci broj 4
– 20 minuta. Domaća zadaća: Domaće zadaće učenici zapisuju u svoje bilježnice. 3 min. Nakon pohađanja seminara o RNS-u i vođenja lekcije pomoću tehnološke karte, postalo mi je očito da sustav ocjenjivanja potiče najveći mogući interes učenika za određenu temu. U mom slučaju to su osnovne formule trigonometrije. Učenici vrlo često ne percipiraju trigonometriju, ne toliko zbog njezine složenosti, koliko zbog velikog broja formula s kojima morate znati raditi. Teško je očekivati neki nevjerojatan napredak i rezultate nakon jednog sata, provedenog pomoću tehnološke karte, ali čini mi se da su prednosti sustava ocjenjivanja u proučavanju trigonometrije i matematike općenito sljedeće: postalo je moguće organizirati i podržavati kako rad u razredu tako i samostalan, sustavan rad učenika kod kuće; trebalo bi povećati pohađanje nastave i razinu discipline u razredu; povećava motivaciju za aktivnosti učenja; smanjuju se stresne situacije pri dobivanju nezadovoljavajućih ocjena; potiče kreativnost u radu. Jedina mana RNS-a (kako mi se čini) je velika količina posla za nastavnika, ali to je rad za rezultat. Nakon jednog sata s ovim sustavom, učenici stalno pitaju hoćemo li nastaviti raditi na ovaj način. Znači da su se na nešto navukli. I trebamo nastaviti raditi. SAMOSTALNI RAD Koju god razinu odabrali, prvo pažljivo pregledaj sve zadatke koje sam ti dao, a zatim dovrši zadatak koji odgovara razini koju si odabrao (pred vama su četiri opcije, broj opcije odgovara razinama samoprocjene.) 1 opcija
Uputa:
Uputa:
Riješite sami ovaj primjer: opcija 2
Napomena: Za određivanje kosinusne funkcije upotrijebite formulu (3) iz današnje lekcije. Ne zaboravite definirati znak koji će biti ispred korijena. Da biste izračunali vrijednosti tangensa i kotangensa, možete koristiti definiciju ovih funkcija ili koristiti formule koje smo danas izveli u lekciji. Uputa. Grupirajte prvi i treći član izraza, stavite u zagradu zajednički faktor .... 3 opcija
4 opcija
Ponavljanje: 1. U kojoj je četvrtini kut 1 radijan i čemu je približno jednak? U prvoj četvrtini 1 rad. 57,3° 2. Koja riječ nedostaje u definiciji funkcije sinus? Sinus kuta
naziva se ………… točkama jedinične kružnice. ORDINATNI 3. Koja riječ nedostaje u definiciji funkcije kosinus? Kosinus kuta
nazvao …………
točke jedinične kružnice. APSCISA 4. Dodajte formulu:
tg
5. Odredite znak proizvoda: tg
6. Koju vrijednost može poprimiti sinus?
ili
7. Izračunajte: g
B(x;y)
R
Y=grijeh
O
x
x=cos
Završi snimanje:
x
g
x
g
x
x
x
g
x
g
x
x
1 opcija: 3 opcija: Opcija 2: 4 opcija:Omjer između tangensa i kotangensa istog kuta
Apscisa bježi.


"Kratki plan"Pogledajte sadržaj dokumenta
"Odraz"Pogledajte sadržaj dokumenta
"Samostalan rad"





Pogledajte sadržaj prezentacije
"Prezentacija"

















