Έννοια παραλληλογράμμου
Ορισμός 1
Παραλληλόγραμμοείναι ένα τετράπλευρο στο οποίο οι απέναντι πλευρές είναι παράλληλες μεταξύ τους (Εικ. 1).
Εικόνα 1.
Ένα παραλληλόγραμμο έχει δύο κύριες ιδιότητες. Ας τα εξετάσουμε χωρίς αποδείξεις.
Ιδιοκτησία 1: Οι απέναντι πλευρές και γωνίες ενός παραλληλογράμμου είναι ίσες, αντίστοιχα.
Ιδιοκτησία 2: Οι διαγώνιες που σχεδιάζονται σε ένα παραλληλόγραμμο διχοτομούνται από το σημείο τομής τους.
Σημάδια παραλληλογράμμου
Ας εξετάσουμε τρία χαρακτηριστικά ενός παραλληλογράμμου και ας τα παρουσιάσουμε με τη μορφή θεωρημάτων.
Θεώρημα 1
Αν δύο πλευρές ενός τετράπλευρου είναι ίσες μεταξύ τους και επίσης παράλληλες, τότε αυτό το τετράπλευρο θα είναι παραλληλόγραμμο.
Απόδειξη.
Ας μας δοθεί ένα τετράπλευρο $ABCD$. Στο οποίο $AB||CD$ και $AB=CD$ Ας σχεδιάσουμε μια διαγώνιο $AC$ σε αυτό (Εικ. 2).

Εικόνα 2.
Εξετάστε τις παράλληλες ευθείες $AB$ και $CD$ και τη διατομή τους $AC$. Τότε
\[\γωνία CAB=\γωνία DCA\]
σαν σταυρωτές γωνίες.
Σύμφωνα με το κριτήριο $I$ ισότητας τριγώνων,
αφού το $AC$ είναι η κοινή τους πλευρά και το $AB=CD$ κατά συνθήκη. Μέσα
\[\γωνία DAC=\γωνία ACB\]
Εξετάστε τις ευθείες $AD$ και $CB$ και την τέμνουσα $AC$ με την τελευταία ισότητα στις κείνουσες γωνίες που λαμβάνουμε ότι $AD||CB$.) Συνεπώς, εξ ορισμού $1$, αυτό το τετράπλευρο είναι παραλληλόγραμμο.
Το θεώρημα έχει αποδειχθεί.
Θεώρημα 2
Αν οι απέναντι πλευρές ενός τετράπλευρου είναι ίσες μεταξύ τους, τότε είναι παραλληλόγραμμο.
Απόδειξη.
Ας μας δοθεί ένα τετράπλευρο $ABCD$. Στο οποίο $AD=BC$ και $AB=CD$. Ας σχεδιάσουμε μια διαγώνιο $AC$ σε αυτό (Εικ. 3).

Εικόνα 3.
Εφόσον τα $AD=BC$, $AB=CD$ και $AC$ είναι μια κοινή πλευρά, τότε με το κριτήριο $III$ για την ισότητα των τριγώνων,
\[\τρίγωνο DAC=\τρίγωνο ACB\]
\[\γωνία DAC=\γωνία ACB\]
Ας εξετάσουμε τις ευθείες $AD$ και $CB$ και την τέμνουσα $AC$ από την τελευταία ισότητα κατά μήκος των γωνιών που βρίσκονται στο $AD||CB$. Επομένως, εξ ορισμού $1$, αυτό το τετράπλευρο είναι ένα παραλληλόγραμμο.
\[\γωνία DCA=\γωνία CAB\]
Ας εξετάσουμε τις ευθείες $AB$ και $CD$ και την τέμνουσα $AC$ με την τελευταία ισότητα κατά μήκος των γωνιών που βρίσκονται στο $AB||CD$. Επομένως, σύμφωνα με τον ορισμό 1, αυτό το τετράπλευρο είναι παραλληλόγραμμο.
Το θεώρημα έχει αποδειχθεί.
Θεώρημα 3
Αν οι διαγώνιοι που σχεδιάζονται σε ένα τετράπλευρο χωρίζονται σε δύο ίσα μέρη από το σημείο τομής τους, τότε αυτό το τετράπλευρο είναι παραλληλόγραμμο.
Απόδειξη.
Ας μας δοθεί ένα τετράπλευρο $ABCD$. Ας σχεδιάσουμε τις διαγώνιες $AC$ και $BD$ σε αυτό. Αφήστε τα να τέμνονται στο σημείο $O$ (Εικ. 4).
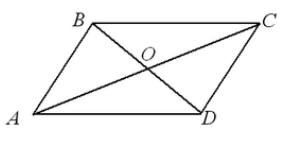
Εικόνα 4.
Εφόσον, κατά συνθήκη, $BO=OD,\ AO=OC$, και οι γωνίες $\γωνία COB=\γωνία DOA$ είναι κάθετες, τότε, με το κριτήριο $I$ για την ισότητα των τριγώνων,
\[\τρίγωνο BOC=\τρίγωνο AOD\]
\[\γωνία DBC=\γωνία BDA\]
Θεωρήστε τις ευθείες $BC$ και $AD$ και την τέμνουσα $BD$ με την τελευταία ισότητα κατά μήκος των γωνιών που βρίσκονται σε αυτό το $BC||AD$. Επίσης $BC=AD$. Επομένως, σύμφωνα με το Θεώρημα $1$, αυτό το τετράπλευρο είναι παραλληλόγραμμο.
Παραλληλόγραμμο είναι ένα τετράπλευρο του οποίου οι απέναντι πλευρές είναι παράλληλες, δηλ. βρίσκονται σε παράλληλες ευθείες
Ιδιότητες παραλληλογράμμου:  Θεώρημα 22.
Οι απέναντι πλευρές ενός παραλληλογράμμου είναι ίσες.
Θεώρημα 22.
Οι απέναντι πλευρές ενός παραλληλογράμμου είναι ίσες.
Απόδειξη. Στο παραλληλόγραμμο ABCD σχεδιάζουμε μια διαγώνιο AC. Τα τρίγωνα ACD και ACB είναι ίσα, καθώς έχουν μια κοινή πλευρά AC και δύο ζεύγη ίσες γωνίες. δίπλα του: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (ως εγκάρσιες γωνίες με παράλληλες ευθείες AD και BC). Αυτό σημαίνει ότι AB = CD και BC = AD, ως αντίστοιχες πλευρές ίσων τριγώνων κ.λπ. Από την ισότητα αυτών των τριγώνων προκύπτει επίσης ότι οι αντίστοιχες γωνίες των τριγώνων είναι ίσες:
Θεώρημα 23.
Οι απέναντι γωνίες του παραλληλογράμμου είναι ίσες: ∠ A=∠ C και ∠ B=∠ D.
Η ισότητα του πρώτου ζεύγους προέρχεται από την ισότητα των τριγώνων ABD και CBD, και του δεύτερου - ABC και ACD.
Θεώρημα 24.
Παρακείμενες γωνίες παραλληλογράμμου, δηλ. Οι γωνίες που γειτνιάζουν με τη μία πλευρά ανέρχονται σε 180 μοίρες.
Αυτό συμβαίνει επειδή είναι εσωτερικές μονόπλευρες γωνίες.
Θεώρημα 25.
Οι διαγώνιοι ενός παραλληλογράμμου διχοτομούνται στο σημείο τομής τους.
Απόδειξη. Εξετάστε τα τρίγωνα BOC και AOD. Σύμφωνα με την πρώτη ιδιότητα AD=BC ∠ OAD=∠ OCB και ∠ ODA=∠ OBC που βρίσκεται σταυρωτά για παράλληλες ευθείες AD και BC. Επομένως, τα τρίγωνα BOC και AOD είναι ίσα σε πλευρικές και γειτονικές γωνίες. Αυτό σημαίνει BO=OD και AO=OS, όπως οι αντίστοιχες πλευρές ίσων τριγώνων κ.λπ.
Σημάδια παραλληλογράμμου
Θεώρημα 26.
Αν οι απέναντι πλευρές ενός τετράπλευρου είναι ίσες σε ζεύγη, τότε είναι παραλληλόγραμμο.
Απόδειξη. Έστω το τετράπλευρο ABCD να έχει πλευρές AD και BC, AB και CD αντίστοιχα ίσες (Εικ. 2). Ας σχεδιάσουμε τη διαγώνιο AC. Τα τρίγωνα ABC και ACD είναι ίσα στις τρεις πλευρές. Τότε οι γωνίες BAC και DCA είναι ίσες και, επομένως, το AB είναι παράλληλο προς το CD. Ο παραλληλισμός των πλευρών BC και AD προκύπτει από την ισότητα των γωνιών CAD και ACB.
Θεώρημα 27.
Αν οι απέναντι γωνίες ενός τετράπλευρου είναι ίσες ανά ζεύγη, τότε είναι παραλληλόγραμμο.
Έστω ∠ A=∠ C και ∠ B=∠ D. Επειδή ∠ A+∠ B+∠ C+∠ D=360 o, μετά ∠ A+∠ B=180 o και οι πλευρές AD και BC είναι παράλληλες (με βάση τον παραλληλισμό των ευθειών). Θα αποδείξουμε επίσης τον παραλληλισμό των πλευρών ΑΒ και ΓΔ και θα συμπεράνουμε ότι το ΑΒΓΔ είναι εξ ορισμού παραλληλόγραμμο.
Θεώρημα 28.
Αν γειτονικές γωνίες τετράπλευρου, π.χ. Οι γωνίες που γειτνιάζουν με τη μία πλευρά αθροίζονται έως και 180 μοίρες, τότε είναι παραλληλόγραμμο.
Εάν οι εσωτερικές μονόπλευρες γωνίες αθροίζονται έως και 180 μοίρες, τότε οι ευθείες γραμμές είναι παράλληλες. Άρα το AB είναι παράλληλο στο CD και το BC είναι παράλληλο στο AD. Ένα τετράπλευρο αποδεικνύεται ότι είναι παραλληλόγραμμο εξ ορισμού.
Θεώρημα 29.
Αν οι διαγώνιοι ενός τετράπλευρου διχοτομούνται μεταξύ τους στο σημείο τομής, τότε το τετράπλευρο είναι παραλληλόγραμμο.
Απόδειξη. Αν AO = OC, BO = OD, τότε τα τρίγωνα AOD και BOC είναι ίσα, καθώς έχουν ίσες (κάθετες) γωνίες στην κορυφή Ο, που περικλείονται μεταξύ ζευγαριών ίσων πλευρών. Από την ισότητα των τριγώνων συμπεραίνουμε ότι AD και BC είναι ίσα. Οι πλευρές AB και CD είναι επίσης ίσες και το τετράπλευρο αποδεικνύεται παραλληλόγραμμο σύμφωνα με το κριτήριο 1.
Θεώρημα 30.
Αν ένα τετράπλευρο έχει ζεύγος ίσων, παράλληλων πλευρών, τότε είναι παραλληλόγραμμο.
Έστω οι πλευρές ΑΒ και ΓΔ του τετραπλεύρου ΑΒΓΔ παράλληλες και ίσες. Ας σχεδιάσουμε τις διαγώνιες AC και BD. Από τον παραλληλισμό αυτών των ευθειών προκύπτει ότι οι εγκάρσιες γωνίες ABO = CDO και BAO = OCD είναι ίσες. Τα τρίγωνα ABO και CDO είναι ίσα σε πλευρικές και γειτονικές γωνίες. Επομένως AO=OS, VO=OD, δηλ. Οι διαγώνιοι διαιρούνται στο μισό με το σημείο τομής και το τετράπλευρο αποδεικνύεται παραλληλόγραμμο σύμφωνα με το κριτήριο 4.
Στη γεωμετρία εξετάζονται ειδικές περιπτώσεις παραλληλογραμμών.
Κατά την επίλυση προβλημάτων σχετικά με αυτό το θέμα, εκτός βασικές ιδιότητες παραλληλόγραμμοκαι τους αντίστοιχους τύπους, μπορείτε να θυμάστε και να εφαρμόσετε τα ακόλουθα:
- Η διχοτόμος εσωτερικής γωνίας παραλληλογράμμου αποκόπτει ένα ισοσκελές τρίγωνο από αυτήν
- Οι διχοτόμοι των εσωτερικών γωνιών που γειτνιάζουν με μία από τις πλευρές ενός παραλληλογράμμου είναι αμοιβαία κάθετες
- Οι διχοτόμοι που προέρχονται από αντίθετες εσωτερικές γωνίες ενός παραλληλογράμμου είναι παράλληλες μεταξύ τους ή βρίσκονται στην ίδια ευθεία
- Το άθροισμα των τετραγώνων των διαγωνίων ενός παραλληλογράμμου είναι ίσο με το άθροισμα των τετραγώνων των πλευρών του
- Το εμβαδόν ενός παραλληλογράμμου είναι ίσο με το μισό γινόμενο των διαγωνίων και του ημιτόνου της μεταξύ τους γωνίας
Ας εξετάσουμε προβλήματα στα οποία χρησιμοποιούνται αυτές οι ιδιότητες.
Εργασία 1.
Η διχοτόμος της γωνίας Γ του παραλληλογράμμου ΑΒΓΔ τέμνει την πλευρά ΑΔ στο σημείο Μ και τη συνέχεια της πλευράς ΑΒ πέρα από το σημείο Α στο σημείο Ε. Να βρείτε την περίμετρο του παραλληλογράμμου αν ΑΕ = 4, ΔΜ = 3.
Διάλυμα.
1. Το τρίγωνο CMD είναι ισοσκελές. (Ακίνητο 1). Επομένως, CD = MD = 3 cm.
2. Το τρίγωνο ΕΑΜ είναι ισοσκελές.
Επομένως, AE = AM = 4 cm.
3. AD = AM + MD = 7 cm.
4. Περίμετρος ΑΒΓΔ = 20 cm.
Απάντηση. 20 εκ.
Εργασία 2.
Οι διαγώνιοι σχεδιάζονται σε ένα κυρτό τετράπλευρο ABCD. Είναι γνωστό ότι τα εμβαδά των τριγώνων ABD, ACD, BCD είναι ίσα. Να αποδείξετε ότι αυτό το τετράπλευρο είναι παραλληλόγραμμο.

Διάλυμα.
1. Έστω BE το ύψος του τριγώνου ABD, CF το ύψος του τριγώνου ACD. Εφόσον, σύμφωνα με τις συνθήκες του προβλήματος, τα εμβαδά των τριγώνων είναι ίσα και έχουν κοινή βάση ΑΔ, τότε τα ύψη αυτών των τριγώνων είναι ίσα. BE = CF.
2. ΒΕ, ΚΦ είναι κάθετα στην ΑΔ. Τα σημεία Β και Γ βρίσκονται στην ίδια πλευρά σε σχέση με την ευθεία ΑΔ. BE = CF. Επομένως, ευθεία π.Χ. || ΔΙΑΦΗΜΙΣΗ. (*)
3. Έστω AL το υψόμετρο τριγώνου ACD, BK το υψόμετρο τριγώνου BCD. Εφόσον, σύμφωνα με τις συνθήκες του προβλήματος, τα εμβαδά των τριγώνων είναι ίσα και έχουν κοινή βάση CD, τότε τα ύψη αυτών των τριγώνων είναι ίσα. AL = ΒΚ.
4. Το AL και το BK είναι κάθετα στο CD. Τα σημεία Β και Α βρίσκονται στην ίδια πλευρά σε σχέση με την ευθεία γραμμή CD. AL = ΒΚ. Επομένως, ευθεία ΑΒ || CD (**)
5. Από τις συνθήκες (*), (**) προκύπτει ότι το ABCD είναι παραλληλόγραμμο.
Απάντηση. Αποδεδειγμένος. Το ABCD είναι παραλληλόγραμμο.
Εργασία 3.
Στις πλευρές BC και CD του παραλληλογράμμου ABCD, σημειώνονται τα σημεία M και H, αντίστοιχα, έτσι ώστε τα τμήματα BM και HD να τέμνονται στο σημείο O.<ВМD = 95 о,
 Διάλυμα.
Διάλυμα.
1. Σε τρίγωνο DOM<МОD = 25 о (Он смежный с <ВОD = 155 о); <ОМD = 95 о. Тогда <ОDМ = 60 о.
2. Σε ορθογώνιο τρίγωνο DHC Τότε<НСD = 30 о. СD: НD = 2: 1 Αλλά CD = AB. Τότε AB: HD = 2: 1. 3. <С = 30 о, 4. <А = <С = 30 о, <В = Απάντηση: AB: HD = 2: 1,<А = <С = 30 о, <В = Εργασία 4. Μία από τις διαγώνιους ενός παραλληλογράμμου με μήκος 4√6 σχηματίζει γωνία 60° με τη βάση και η δεύτερη διαγώνιος σχηματίζει γωνία 45° με την ίδια βάση. Βρείτε τη δεύτερη διαγώνιο. Διάλυμα.
1. AO = 2√6. 2. Εφαρμόζουμε το ημιτονικό θεώρημα στο τρίγωνο AOD. AO/sin D = OD/sin A. 2√6/sin 45 o = OD/sin 60 o. ОD = (2√6sin 60 о) / sin 45 о = (2√6 √3/2) / (√2/2) = 2√18/√2 = 6. Απάντηση: 12.
Εργασία 5. Για παραλληλόγραμμο με πλευρές 5√2 και 7√2, η μικρότερη γωνία μεταξύ των διαγωνίων είναι ίση με τη μικρότερη γωνία του παραλληλογράμμου. Να βρείτε το άθροισμα των μηκών των διαγωνίων. Διάλυμα.
Έστω d 1, d 2 οι διαγώνιοι του παραλληλογράμμου και η γωνία μεταξύ των διαγωνίων και της μικρότερης γωνίας του παραλληλογράμμου είναι ίση με φ. 1. Ας μετρήσουμε δύο διαφορετικά S ABCD = AB AD sin A = 5√2 7√2 sin f, S ABCD = 1/2 AC ВD sin AOB = 1/2 d 1 d 2 sin f. Λαμβάνουμε την ισότητα 5√2 · 7√2 · sin f = 1/2d 1 d 2 sin f ή 2 · 5√2 · 7√2 = d 1 d 2 ; 2. Χρησιμοποιώντας τη σχέση μεταξύ των πλευρών και των διαγωνίων του παραλληλογράμμου, γράφουμε την ισότητα (AB 2 + AD 2) 2 = AC 2 + BD 2. ((5√2) 2 + (7√2) 2) 2 = d 1 2 + d 2 2. d 1 2 + d 2 2 = 296. 3. Ας δημιουργήσουμε ένα σύστημα: (d 1 2 + d 2 2 = 296, Ας πολλαπλασιάσουμε τη δεύτερη εξίσωση του συστήματος επί 2 και ας την προσθέσουμε στην πρώτη. Παίρνουμε (d 1 + d 2) 2 = 576. Επομένως Id 1 + d 2 I = 24. Επειδή τα d 1, d 2 είναι τα μήκη των διαγωνίων του παραλληλογράμμου, τότε d 1 + d 2 = 24. Απάντηση: 24.
Εργασία 6. Οι πλευρές του παραλληλογράμμου είναι 4 και 6. Η οξεία γωνία μεταξύ των διαγωνίων είναι 45 μοίρες. Βρείτε το εμβαδόν του παραλληλογράμμου. Διάλυμα.
1. Από το τρίγωνο ΑΟΒ, χρησιμοποιώντας το θεώρημα συνημιτόνου, γράφουμε τη σχέση μεταξύ της πλευράς του παραλληλογράμμου και των διαγωνίων. AB 2 = AO 2 + VO 2 2 · AO · VO · cos AOB. 4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1/2) · (d 2 /2)cos 45 o; d 1 2 /4 + d 2 2 /4 – 2 (d 1 /2) (d 2 /2)√2/2 = 16. d 1 2 + d 2 2 – d 1 · d 2 √2 = 64. 2. Ομοίως γράφουμε τη σχέση για το τρίγωνο ΑΟΔ. Ας το λάβουμε υπόψη<АОD = 135 о и cos 135 о = -cos 45 о = -√2/2. Παίρνουμε την εξίσωση d 1 2 + d 2 2 + d 1 · d 2 √2 = 144. 3. Έχουμε σύστημα Αφαιρώντας την πρώτη από τη δεύτερη εξίσωση, παίρνουμε 2d 1 · d 2 √2 = 80 ή d 1 d 2 = 80/(2√2) = 20√2 4. S ABCD = 1/2 AC ВD sin AOB = 1/2 d 1 d 2 sin α = 1/2 20√2 √2/2 = 10. Σημείωμα:Σε αυτό και στο προηγούμενο πρόβλημα δεν χρειάζεται να λυθεί πλήρως το σύστημα, προβλέποντας ότι σε αυτό το πρόβλημα χρειαζόμαστε το γινόμενο των διαγωνίων για να υπολογίσουμε το εμβαδόν. Απάντηση: 10. Εργασία 7. Το εμβαδόν του παραλληλογράμμου είναι 96 και οι πλευρές του είναι 8 και 15. Βρείτε το τετράγωνο της μικρότερης διαγωνίου. Διάλυμα.
1. S ABCD = AB · AD · sin VAD. Ας κάνουμε μια αντικατάσταση στον τύπο. Παίρνουμε 96 = 8 · 15 · sin VAD. Ως εκ τούτου αμαρτία VAD = 4/5. 2. Ας βρούμε το cos VAD. sin 2 VAD + cos 2 VAD = 1. (4 / 5) 2 + cos 2 VAD = 1. cos 2 VAD = 9 / 25. Σύμφωνα με τις συνθήκες του προβλήματος, βρίσκουμε το μήκος της μικρότερης διαγωνίου. Η διαγώνιος ΒD θα είναι μικρότερη εάν η γωνία ВАD είναι οξεία. Τότε cos VAD = 3 / 5. 3. Από το τρίγωνο ΑΒΔ, χρησιμοποιώντας το θεώρημα συνημιτόνου, βρίσκουμε το τετράγωνο της διαγωνίου ΒΔ. ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos BAD. ВD 2 = 8 2 + 15 2 – 2 8 15 3 / 5 = 145. Απάντηση: 145.
Έχετε ακόμα ερωτήσεις; Δεν ξέρετε πώς να λύσετε ένα πρόβλημα γεωμετρίας; ιστοσελίδα, όταν αντιγράφετε υλικό εν όλω ή εν μέρει, απαιτείται σύνδεσμος προς την αρχική πηγή. Παραλληλόγραμμο είναι ένα τετράπλευρο του οποίου οι απέναντι πλευρές είναι παράλληλες ανά ζεύγη. Το παρακάτω σχήμα δείχνει το παραλληλόγραμμο ABCD. Έχει την πλευρά ΑΒ παράλληλη προς την πλευρά CD και την πλευρά BC παράλληλη στην πλευρά ΑΔ. Όπως ίσως έχετε μαντέψει, ένα παραλληλόγραμμο είναι ένα κυρτό τετράπλευρο. Ας εξετάσουμε τις βασικές ιδιότητες ενός παραλληλογράμμου. 1. Σε ένα παραλληλόγραμμο οι απέναντι γωνίες και οι απέναντι πλευρές είναι ίσες. Ας αποδείξουμε αυτήν την ιδιότητα - θεωρήστε το παραλληλόγραμμο που παρουσιάζεται στο παρακάτω σχήμα. Η διαγώνια BD τη χωρίζει σε δύο ίσα τρίγωνα: ABD και CBD. Είναι ίσες κατά μήκος της πλευράς BD και των δύο παρακείμενων γωνιών, αφού οι γωνίες που βρίσκονται εγκάρσια στην τέμνουσα BD των παράλληλων ευθειών BC και AD και AB και CD, αντίστοιχα. Επομένως ΑΒ = CD και 2. Οι διαγώνιοι ενός παραλληλογράμμου διαιρούνται στο μισό με το σημείο τομής. Έστω σημείο Ο το σημείο τομής των διαγωνίων AC και BD του παραλληλογράμμου ABCD. Τότε το τρίγωνο AOB και το τρίγωνο COD είναι ίσα μεταξύ τους, κατά μήκος της πλευράς και δύο παρακείμενες γωνίες. (AB = CD δεδομένου ότι αυτές είναι αντίθετες πλευρές του παραλληλογράμμου. Και η γωνία 1 = γωνία 2 και η γωνία 3 = γωνία 4 είναι σαν εγκάρσιες γωνίες όταν οι ευθείες AB και CD τέμνονται με τις τομές AC και BD, αντίστοιχα.) Από αυτό προκύπτει ότι AO = OC και OB = OD, τα οποία και έπρεπε να αποδειχθούν. Όλες οι κύριες ιδιότητες απεικονίζονται στα ακόλουθα τρία σχήματα. «Μια μεγάλη επιστημονική ανακάλυψη δίνει λύση σε ένα μεγάλο πρόβλημα, αλλά στη λύση κάθε προβλήματος υπάρχει ένας κόκκος ανακάλυψης». Ένα παραλληλόγραμμο έχει απέναντι πλευρές που είναι ίσες. Απόδειξη. Έστω ABCD το δεδομένο παραλληλόγραμμο. Και αφήστε τις διαγώνιές του να τέμνονται στο σημείο Ο. Σε ένα παραλληλόγραμμο οι απέναντι γωνίες είναι ίσες. Απόδειξη. Οι διαγώνιοι ενός παραλληλογράμμου τέμνονται και διχοτομούνται στο σημείο τομής. Απόδειξη. Έστω ABCD το δεδομένο παραλληλόγραμμο. Ας σχεδιάσουμε τη διαγώνιο AC. Ας σημειώσουμε το μεσαίο O στη συνέχεια του τμήματος DO, θα αφήσουμε στην άκρη το τμήμα OB 1 ίσο με DO. Στα σχολικά βιβλία για τα κανονικά σχολεία (για παράδειγμα, στο Pogorelovo) αποδεικνύεται ως εξής: οι διαγώνιοι χωρίζουν ένα παραλληλόγραμμο σε 4 τρίγωνα. Ας εξετάσουμε ένα ζευγάρι και ας μάθουμε - είναι ίσες: οι βάσεις τους είναι απέναντι πλευρές, οι αντίστοιχες γωνίες που γειτνιάζουν με αυτό είναι ίσες, όπως κάθετες γωνίες με παράλληλες γραμμές. Δηλαδή, τα τμήματα των διαγωνίων είναι ίσα σε ζεύγη. Ολοι. Αυτό είναι όλο; Το αστείο είναι ότι αυτό το κομμάτι είναι πολύ πιο δύσκολο να αποδειχτεί. Αυτό προκύπτει, παρεμπιπτόντως, από ένα γενικότερο αποτέλεσμα: κάθε κυρτό τετράπλευρο θα έχει διαγώνιες που τέμνονται, αλλά κάθε μη κυρτό τετράπλευρο δεν θα έχει. Σχετικά με την ισότητα των τριγώνων κατά μήκος μιας πλευράς και δύο παρακείμενων γωνιών (το δεύτερο σημάδι ισότητας τριγώνων) και άλλα. Ο Θαλής βρήκε μια σημαντική πρακτική εφαρμογή στο θεώρημα της ισότητας δύο τριγώνων κατά μήκος μιας πλευράς και δύο γειτονικών γωνιών. Στο λιμάνι της Μιλήτου κατασκευάστηκε αποστασιόμετρο για να προσδιορίσει την απόσταση από ένα πλοίο στη θάλασσα. Αποτελούνταν από τρεις κινούμενους γόμφους A, B και C (AB = BC) και μια σημειωμένη ευθεία γραμμή SC, κάθετη στην CA. Όταν ένα πλοίο εμφανιζόταν στην ευθεία SK, βρήκαμε το σημείο D τέτοιο ώστε τα σημεία D, .B και E να βρίσκονται στην ίδια ευθεία. Όπως φαίνεται από το σχέδιο, η απόσταση CD στο έδαφος είναι η επιθυμητή απόσταση από το πλοίο. Δουλέψαμε στο μάθημα Kuznetsov A.V. Poturnak S.A. Evgeniy Petrov Μπορείτε να θέσετε μια ερώτηση σχετικά με τη σύγχρονη εκπαίδευση, να εκφράσετε μια ιδέα ή να λύσετε ένα πιεστικό πρόβλημα στο Εκπαιδευτικό φόρουμ, όπου ένα εκπαιδευτικό συμβούλιο φρέσκιας σκέψης και δράσης συνεδριάζει διεθνώς. Έχοντας δημιουργήσει blog,Δεν θα βελτιώσετε μόνο την κατάστασή σας ως ικανός δάσκαλος, αλλά και θα συμβάλετε σημαντικά στην ανάπτυξη του σχολείου του μέλλοντος. Συντεχνία Εκπαιδευτικών Ηγετώνανοίγει πόρτες σε κορυφαίους ειδικούς και τους προσκαλεί να συνεργαστούν για τη δημιουργία των καλύτερων σχολείων στον κόσμο.
(
(Δεδομένου ότι σε ένα ορθογώνιο τρίγωνο το σκέλος που βρίσκεται απέναντι από τη γωνία των 30° είναι ίσο με τη μισή υποτείνουσα).
 τρόπους περιοχής του.
τρόπους περιοχής του.
(d 1 + d 2 = 140.
(d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Για να λάβετε βοήθεια από έναν δάσκαλο, εγγραφείτε.
Το πρώτο μάθημα είναι δωρεάν!
Ιδιότητες παραλληλογράμμου

π.Χ. = μ.Χ. Και από την ισότητα των γωνιών 1, 2, 3 και 4 προκύπτει ότι γωνία Α = γωνία1 + γωνία3 = γωνία2 + γωνία 4 = γωνία Γ.
Θέμα μαθήματος
Στόχοι μαθήματος
Στόχοι μαθήματος
Σχέδιο μαθήματος
Εισαγωγή

Ιδιότητα των απέναντι πλευρών παραλληλογράμμου
Αφού Δ AOB = Δ COD με το πρώτο κριτήριο ισότητας τριγώνων (∠ AOB = ∠ COD, ως κατακόρυφα, AO=OC, DO=OB, από την ιδιότητα των διαγωνίων ενός παραλληλογράμμου), τότε AB=CD. Με τον ίδιο τρόπο, από την ισότητα των τριγώνων BOC και DOA, προκύπτει ότι BC = DA. Το θεώρημα έχει αποδειχθεί. Ιδιότητα απέναντι γωνιών παραλληλογράμμου
Έστω ABCD το δεδομένο παραλληλόγραμμο. Και αφήστε τις διαγώνιές του να τέμνονται στο σημείο Ο.
Από όσα αποδείχθηκαν στο θεώρημα για τις ιδιότητες των απέναντι πλευρών ενός παραλληλογράμμου Δ ABC = Δ CDA σε τρεις πλευρές (AB=CD, BC=DA από ότι αποδείχθηκε, AC – γενική). Από την ισότητα των τριγώνων προκύπτει ότι ∠ ABC = ∠ CDA.
Αποδεικνύεται επίσης ότι ∠ DAB = ∠ BCD, που προκύπτει από το ∠ ABD = ∠ CDB. Το θεώρημα έχει αποδειχθεί.Ιδιότητα των διαγωνίων παραλληλογράμμου
Σύμφωνα με το προηγούμενο θεώρημα, το AB 1 CD είναι ένα παραλληλόγραμμο. Επομένως, η ευθεία AB 1 είναι παράλληλη με το DC. Αλλά μέσω του σημείου Α μπορεί να σχεδιαστεί μόνο μία ευθεία παράλληλη προς το DC. Αυτό σημαίνει ότι η ευθεία ΑΒ 1 συμπίπτει με την ευθεία ΑΒ.
Αποδεικνύεται επίσης ότι το 1 π.Χ. συμπίπτει με το π.Χ. Αυτό σημαίνει ότι το σημείο C συμπίπτει με το C 1. το παραλληλόγραμμο ABCD συμπίπτει με το παραλληλόγραμμο AB 1 CD. Κατά συνέπεια, οι διαγώνιοι του παραλληλογράμμου τέμνονται και διχοτομούνται στο σημείο τομής. Το θεώρημα έχει αποδειχθεί.
Αποδείχθηκε παραπάνω ότι το σημείο τομής διχοτομεί τις διαγώνιες - αν υπάρχει. Ο παραπάνω συλλογισμός δεν αποδεικνύει με κανένα τρόπο την ίδια την ύπαρξή του. Δηλαδή, μέρος του θεωρήματος «οι διαγώνιοι ενός παραλληλογράμμου τέμνονται» παραμένει αναπόδεικτο.
Ερωτήσεις
Κατάλογος πηγών που χρησιμοποιήθηκαν


